
2.导数的几何意义
函数y=f(x)在点x 处的导数的几何意义是曲线y=f(x)在点p(x
处的导数的几何意义是曲线y=f(x)在点p(x ,f(x
,f(x ))处的切线的斜率。也就是说,曲线y=f(x)在点p(x
))处的切线的斜率。也就是说,曲线y=f(x)在点p(x ,f(x
,f(x ))处的切线的斜率是f’(x
))处的切线的斜率是f’(x )。相应地,切线方程为y-y
)。相应地,切线方程为y-y =f/(x
=f/(x )(x-x
)(x-x )。
)。
1.导数的概念
函数y=f(x),如果自变量x在x 处有增量
处有增量 ,那么函数y相应地有增量
,那么函数y相应地有增量 =f(x
=f(x +
+ )-f(x
)-f(x ),比值
),比值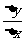 叫做函数y=f(x)在x
叫做函数y=f(x)在x 到x
到x +
+ 之间的平均变化率,即
之间的平均变化率,即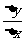 =
= 。如果当
。如果当 时,
时,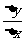 有极限,我们就说函数y=f(x)在点x
有极限,我们就说函数y=f(x)在点x 处可导,并把这个极限叫做f(x)在点x
处可导,并把这个极限叫做f(x)在点x 处的导数,记作f’(x
处的导数,记作f’(x )或y’|
)或y’| 。
。
即f(x )=
)=
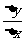 =
=
 。
。
说明:
求函数y=f(x)在点x 处的导数的步骤:
处的导数的步骤:
(1)求函数的增量 =f(x
=f(x +
+ )-f(x
)-f(x );
);
(2)求平均变化率 =
= ;
;
(3)取极限,得导数f’(x )=
)= 。
。
15.(07广东)已知 是实数,函数
是实数,函数 .如果函数
.如果函数 在区间
在区间 上有零点,求
上有零点,求 的取值范围.
的取值范围.
14.(07福建)设函数 .
.
(Ⅰ)求 的最小值
的最小值 ;
;
(Ⅱ)若 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
13.(07江苏)已知函数 在区间
在区间 上的最大值与最小值分别为
上的最大值与最小值分别为 ,则
,则
12.(07广东)函数 的单调递增区间是
的单调递增区间是
11. (07北京) 是
是 的导函数,则
的导函数,则 的值是
的值是
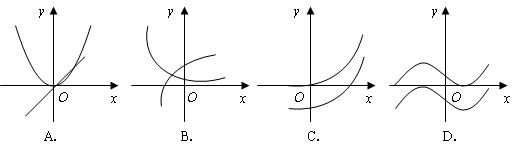
10.(07浙江)设 是函数
是函数 的导函数,将
的导函数,将 和
和 的图象画在同一个直角坐标系中,不可能正确的是( )
的图象画在同一个直角坐标系中,不可能正确的是( )
9.(07全国二)已知曲线 的一条切线的斜率为
的一条切线的斜率为 ,则切点的横坐标为( )
,则切点的横坐标为( )
A.1 B.2 C.3 D.4
8.(07全国一)曲线 在点
在点 处的切线与坐标轴围成的三角形面积为( )
处的切线与坐标轴围成的三角形面积为( )
A. B.
B. C.
C. D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com