

4.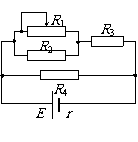 变化电路的讨论。
变化电路的讨论。
闭合电路中只要有一只电阻的阻值发生变化,就会影响整个电路,使总电路和每一部分的电流、电压都发生变化。讨论依据是:闭合电路欧姆定律、部分电路欧姆定律、串联电路的电压关系、并联电路的电流关系。以右图电路为例:设R1增大,总电阻一定增大;由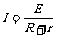 ,I一定减小;由U=E-Ir,U一定增大;因此U4、I4一定增大;由I3= I-I4,I3、U3一定减小;由U2=U-U3,U2、I2一定增大;由I1=I3
-I2,I1一定减小。总结规律如下:
,I一定减小;由U=E-Ir,U一定增大;因此U4、I4一定增大;由I3= I-I4,I3、U3一定减小;由U2=U-U3,U2、I2一定增大;由I1=I3
-I2,I1一定减小。总结规律如下:
①总电路上R增大时总电流I减小,路端电压U增大;②变化电阻本身和总电路变化规律相同;③和变化电阻有串联关系(通过变化电阻的电流也通过该电阻)的看电流(即总电流减小时,该电阻的电流、电压都减小);④和变化电阻有并联关系的(通过变化电阻的电流不通过该电阻)看电压(即路端电压增大时,该电阻的电流、电压都增大)。
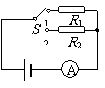 [例题17]如图,电源的内阻不可忽略。已知定值电阻R1=10Ω,R2=8Ω。当电键S接位置1时,电流表的示数为0.20A。那么当电键S接位置2时,电流表的示数可能是下列哪些值
[例题17]如图,电源的内阻不可忽略。已知定值电阻R1=10Ω,R2=8Ω。当电键S接位置1时,电流表的示数为0.20A。那么当电键S接位置2时,电流表的示数可能是下列哪些值
A.0.28A B.0.25A C.0.22A D.0.19A
解:电键接2后,电路的总电阻减小,总电流一定增大,所以不可能是0.19A.电源的路端电压一定减小,原来路端电压为2V,所以电键接2后路端电压低于2V,因此电流一定小于0.25A。所以只能选C。
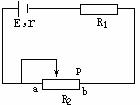 [例题18]如图所示的直流电路中,电源电动势为E,内阻为r,外电路中,电阻R1=r,滑动变阻器的全部电阻为R2=2r,滑动片从a端向b端滑动过程中,哪种说法正确
[例题18]如图所示的直流电路中,电源电动势为E,内阻为r,外电路中,电阻R1=r,滑动变阻器的全部电阻为R2=2r,滑动片从a端向b端滑动过程中,哪种说法正确
A.电源的转化功率逐渐增大
B.电源内部的热功率逐渐增大
C.电源的输出功率逐渐减小
D.R2上得到的功率逐渐减小
解:当滑片P由a向b滑动时,外电路电阻逐渐减小,因此电流逐渐增大,可知选项A、B正确;当滑片P滑到b端时,外电路电阻等于R1与内阻相同,此时电源输出功率最大。此,C不正确;判断D选项时,可把R1看成内阻的一部分,即内阻为2r,因此当P处于a端时,外阻=内阻=2r,此时R2上的功率最大,所以选项D正确。
[例题19]如图所示,电源电动势为E,内电阻为r。当滑动变阻器的触片P从右端滑到左端时,发现电压表V1、V2示数变化的绝对值分别为ΔU1和ΔU2,下列说法中正确的是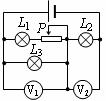
A.小灯泡L1、L3变暗,L2变亮
B.小灯泡L3变暗,L1、L2变亮
C.ΔU1<ΔU2
D.ΔU1>ΔU2
解:滑动变阻器的触片P从右端滑到左端,总电阻减小,总电流增大,路端电压减小。与电阻蝉联串联的灯泡L1、L2电流增大,变亮,与电阻并联的灯泡L3电压降低,变暗。U1减小,U2增大,而路端电压U= U1+ U2减小,所以U1的变化量大于 U2的变化量,选BD。
3.电源的功率和效率
(1)功率:①电源的功率(电源的总功率):指非静电力做功,把其它形式的能转化为电能的功率。PE=EI
 ②电源的输出功率:指电源对外电路做功的功率P出=UI
②电源的输出功率:指电源对外电路做功的功率P出=UI
③电源内部消耗的功率:指内阻上的电热功率.设内阻为r,则Pr=I 2r
这三者之间是什么关系?
(2)电源的效率: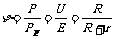 (最后一个等号只适用于纯电阻电路)
(最后一个等号只适用于纯电阻电路)
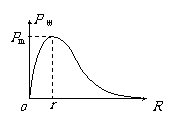
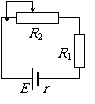 电源的输出功率
电源的输出功率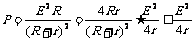 ,则电源输出功率随外电阻变化的图线如图所示,而当内外电阻相等时,电源的输出功率最大,为
,则电源输出功率随外电阻变化的图线如图所示,而当内外电阻相等时,电源的输出功率最大,为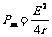 。可见,R越大,电源效率较高,而P出最大时,η=r/(2r)=50%,并不大。所以要注意区分电源输出功率与效率这两个概念。
。可见,R越大,电源效率较高,而P出最大时,η=r/(2r)=50%,并不大。所以要注意区分电源输出功率与效率这两个概念。
[例题16]已知如图,E =6V,r =4Ω,R1=2Ω,R2的变化范围是0~10Ω。求:①电源的最大输出功率;②R1上消耗的最大功率;③R2上消耗的最大功率。
解:①R2=2Ω时,外电阻等于内电阻,电源输出功率最大为2.25W;②R1是定植电阻,电流越大功率越大,所以R2=0时R1上消耗的功率最大为2W;③把R1也看成电源的一部分,等效电源的内阻为6Ω,所以,当R2=6Ω时,R2上消耗的功率最大为1.5W。
2.欧姆定律适用条件
如图所示:电路由电源和电动机组成,电动机绕线电阻为R,则此电路中的电流是否为I=E/(R+r)?
I≠E/(R+r)的关键是U≠IR,即非纯电阻电路中欧姆定律已不再适用。但可由能量分配关系得出表达式E=U+Ir(U为电动机两端的电压)
回答时应提醒学生注意电动机的特点:为非纯电阻用电器,引导学生做出否定回答,即:I≠E/(R+r)
1.主要物理量。
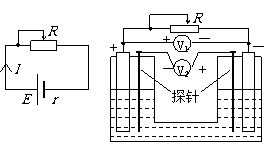 研究闭合电路,主要物理量有E、r、R、I、U,前两个是常量,后三个是变量。
研究闭合电路,主要物理量有E、r、R、I、U,前两个是常量,后三个是变量。
闭合电路欧姆定律的表达形式有:
①E=U外+U内 ②
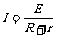 (I、R关系)
(I、R关系)
③U=E-Ir(U、I关系) ④ 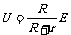 (U、R关系)
(U、R关系)
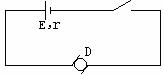 从③式看出:当外电路断开时(I = 0),路端电压等于电动势。而这时用电压表去测量时,读数却应该略小于电动势(有微弱电流)。当外电路短路时(R = 0,因而U = 0)电流最大为Im=E/r(一般不允许出现这种情况,会把电源烧坏)。
从③式看出:当外电路断开时(I = 0),路端电压等于电动势。而这时用电压表去测量时,读数却应该略小于电动势(有微弱电流)。当外电路短路时(R = 0,因而U = 0)电流最大为Im=E/r(一般不允许出现这种情况,会把电源烧坏)。
5.电路中的电表
我们接触比较多的电表是电压表和电流表,理想情况下电流表可以看成导线,电压表可以看成无穷大的电阻而忽略它们的内阻对电路的影响,可在某些实际问题中,这种影响很大,根本不可能忽略不计.这时就要把电表看成一个可以读数的特殊电阻,放在电路中,与其它用电器一起分析。
[例题15]如图所示,R1=2kΩ,R2=3kΩ,电源内阻可忽略。现用一电压表测电路端电压,示数为6V;用这电压表测R1两端,电压示数为2V。那么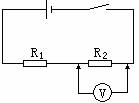
A.R1两端实际电压是2V
B.电压表内阻为6kΩ
C.R2两端实际电压是3.6V
D.用这电压表测R2两端电压,示数是3V
解:本题中电阻R1、R2的阻值较大,电压表与之相比不能看成电阻为无穷大的断路.因此要把它当成一个特殊电阻来处理。
由于不计电源内阻,电压表测得的电压6V就是电源电动势,所以R1两端实际电压为U1=6V×2kΩ/(2kΩ+3kΩ)
同理,U2=3.6V。
当电压表测R1两端电压时,显示的是它与R1并联后所分得的电压,即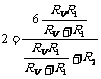 ,所以 RV=6kΩ。
,所以 RV=6kΩ。
当电压表测R2两端电压时,易得电压表示数为3V。所以选项B、C、D正确。
4.电路中有关电容器的计算。
(1)电容器跟与它并联的用电器的电压相等。
(2)在计算出电容器的带电量后,必须同时判定两板的极性,并标在图上。
(3)在充放电时,电容器两根导线上的电流方向总是相同的,所以要根据正极板电荷变化情况来判断电流方向。
(4)如果变化前后极板带电的电性相同,那么通过每根导线的电荷量等于始末状态电容器电荷量的差;如果变化前后极板带电的电性改变,那么通过每根导线的电荷量等于始末状态电容器电荷量之和。
[例题12]已知如图,电源内阻不计。为使电容器的带电量增大,可采取以下那些方法:
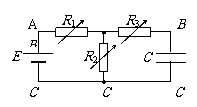 A.增大R1 B.增大R2 C.增大R3 D.减小R1
A.增大R1 B.增大R2 C.增大R3 D.减小R1
解:由于稳定后电容器相当于断路,因此R3上无电流,电容器相当于和R2并联。只有增大R2或减小R1才能增大电容器C两端的电压,从而增大其带电量。改变R3不能改变电容器的带电量。因此选BD。
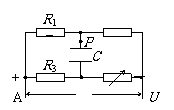 [例题13]已知如图,R1=30Ω,R2=15Ω,R3=20Ω,AB间电压U=6V,A端为正C=2μF,为使电容器带电量达到Q =2×10- 6C,应将R4的阻值调节到多大?
[例题13]已知如图,R1=30Ω,R2=15Ω,R3=20Ω,AB间电压U=6V,A端为正C=2μF,为使电容器带电量达到Q =2×10- 6C,应将R4的阻值调节到多大?
解:由于R1 和R2串联分压,可知R1两端电压一定为4V,由电容器的电容知:为使C的带电量为2×10-6C,其两端电压必须为1V,所以R3的电压可以为3V或5V。因此R4应调节到20Ω或4Ω。两次电容器上极板分别带负电和正电。
还可以得出:当R4由20Ω逐渐减小的到4Ω的全过程中,通过图中P点的电荷量应该是4×10-6C,电流方向为向下。
[例题14]如图示,电源电动势E=12V,内阻r=1Ω,电阻R1=3Ω,R2=2Ω,R3=5Ω,电容器的电容C1=4μF,C2=1μF,求C1、C2所带电量。
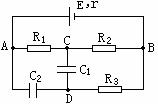 解:C1、C2看成短路后,外电路相当于R1、R2串联,R3中无电流,可视为短路,即UCD=UCB,UAD=UAB,由闭合电路欧姆定律知:
解:C1、C2看成短路后,外电路相当于R1、R2串联,R3中无电流,可视为短路,即UCD=UCB,UAD=UAB,由闭合电路欧姆定律知:
UCB=R2E/(R1 +R2+r)=4V
UAB=(R1+R2)E/(R1 +R2+r)=10V
所以C1、C2所带电量Q1、Q2分别为:Q1=C1UCB=1.6×10-5C;Q2=C2UAB=1×10-5C
3.对复杂电路分析,一般情况下用等势点法比较方便简洁。
(1)凡用导线直接连接的各点的电势必相等(包括用不计电阻的电流表连接的点)。
(2)在外电路,沿着电流方向电势降低。
(3)凡接在同样两个等势点上的电器为并联关系。
(4)不加声明的情况下,不考虑电表对电路的影响。
搞清电路各元件之间的连接关系,画出结构清晰的等效电路,是利用欧姆定律解决电路问题的重要前提。我们通常采用节点跨接法来分析电路结构。
具体方法为:首先标明电路中各节点名称,经过电源和用电器的节点名称应不同,而一段导线两端的节点名称不变。理想的电压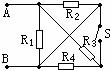 表可视为断路。理想的电流表可视为导线。考虑电表内阻时,就应把它们当作用电器对待。接着,定性判断电路中各节点电势高低(没有标明的可假设)。最后将各电器填在对应的节点间以判明彼此间的串、并联关系。
表可视为断路。理想的电流表可视为导线。考虑电表内阻时,就应把它们当作用电器对待。接着,定性判断电路中各节点电势高低(没有标明的可假设)。最后将各电器填在对应的节点间以判明彼此间的串、并联关系。
[例题11]如右图所示,设R1=R2=R3=R4=R,求:开关S闭合和开启时的AB两端的电阻比。
解:利用节点法,开关闭合时,电路中各节点标称如图a所示。
其中R1、R2、R3都接在AB两点间,而R4两端都为B,即R4被短路,所以其等效电路如图b所示,易得RAB=R/3。
当开关开启时,电路中各节点标称如图c所示,其对应等效电路为图d所示,易得RAB′=2R/5。所以两次电阻比为5/6。

2.公式选取的灵活性。
(1)计算电流,除了用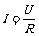 外,还经常用并联电路总电流和分电流的关系:I=I1+I2
外,还经常用并联电路总电流和分电流的关系:I=I1+I2
(2)计算电压,除了用U=IR外,还经常用串联电路总电压和分电压的关系:U=U1+U2
(3)计算电功率,无论串联、并联还是混联,总功率都等于各电阻功率之和:P=P1+P2
对纯电阻,电功率的计算有多种方法:P=UI=I2R=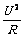
以上公式I=I1+I2、U=U1+U2和P=P1+P2既可用于纯电阻电路,也可用于非纯电阻电路;既可以用于恒定电流,也可用于交变电流。
[例题7]已知如图,R1=6Ω,R2=3Ω,R3=4Ω,则接入电路后这三只电阻的实际功率之比为_________。
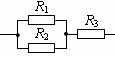 解:本题解法很多,注意灵活、巧妙。经过观察发现三只电阻的电流关系最简单:电流之比是I1∶I2∶I3=1∶2∶3;还可以发现左面两只电阻并联后总阻值为2Ω,因此电压之比是U1∶U2∶U3=1∶1∶2;在此基础上利用P=UI,得P1∶P2∶P3=1∶2∶6
解:本题解法很多,注意灵活、巧妙。经过观察发现三只电阻的电流关系最简单:电流之比是I1∶I2∶I3=1∶2∶3;还可以发现左面两只电阻并联后总阻值为2Ω,因此电压之比是U1∶U2∶U3=1∶1∶2;在此基础上利用P=UI,得P1∶P2∶P3=1∶2∶6
[例题8]已知如图,两只灯泡L1、L2分别标有“110V,60W”和“110V,100W”,另外有一只滑动变阻器R,将它们连接后接入220V的电路中,要求两灯泡都正常发光,并使整个电路消耗的总功率最小,应使用下面哪个电路?
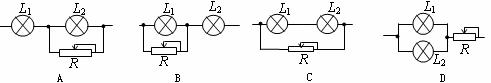
解:A、C两图中灯泡不能正常发光。B、D中两灯泡都能正常发光,它们的特点是左右两部分的电流、电压都相同,因此消耗的电功率一定相等。可以直接看出:B图总功率为200W,D图总功率为320W,所以选B。
[例题9]实验表明,通过某种金属氧化物制成的均匀棒中的电流I跟电压U之间遵循I =kU 3的规律,其中U表示棒两端的电势差,k=0.02A/V3。现将该棒与一个可变电阻器R串联在一起后,接在一个内阻可以忽略不计,电动势为6.0V的电源上。求:(1)当串联的可变电阻器阻值R多大时,电路中的电流为0.16A?(2)当串联的可变电阻器阻值R多大时,棒上消耗的电功率是电阻R上消耗电功率的1/5?
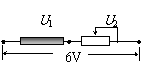 解:画出示意图如右。(1)由I =kU 3和I=0.16A,可求得棒两端电压为2V,因此变阻器两端电压为4V,由欧姆定律得阻值为25Ω。
解:画出示意图如右。(1)由I =kU 3和I=0.16A,可求得棒两端电压为2V,因此变阻器两端电压为4V,由欧姆定律得阻值为25Ω。
(2)由于棒和变阻器是串联关系,电流相等,电压跟功率成正比,棒两端电压为1V,由I =kU3得电流为0.02A,变阻器两端电压为5V,因此电阻为250Ω。
[例题10]左图甲为分压器接法电路图,电源电动势为E,内阻不计,变阻器总电阻为r。闭合电键S后,负载电阻R两端的电压U随变阻器a、b两点间的阻值Rx变化的图线应最接近于右图中的哪条实线
A.① B.② C.③ D.④
解:当Rx增大时,左半部分总电阻增大,右半部分电阻减小,所以R两端的电压U应增大,排除④;如果没有并联R,电压均匀增大,图线将是②;实际上并联了R,对应于同一个Rx值,左半部分分得的电压将比原来小了,所以③正确,选C。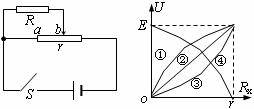
1.应用欧姆定律须注意对应性。
选定研究对象电阻R后,I必须是通过这只电阻R的电流,U必须是这只电阻R两端的电压。该公式只能直接用于纯电阻电路,不能直接用于含有电动机、电解槽等用电器的电路。
5.电功和电热
(1)电路中的功与能
能的转化和守恒定律是自然界普遍适用的规律。电源是把其它能转化为电能的装置,内阻和用电器是电能转化为热能等其它形式能的装置。如化学电池将化学能转化成电能,而电路中发光灯泡是将电能转化成光、热能,如图所示电路。
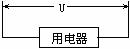 对于一个闭合电路,它的能量应该是守恒的,但又在不同形式间转化,通过做功方式完成。在电源部分,非静电力做正功W非=qE,将其它形式的能转化成电能。而内阻上电流做功,将电能转化成内能W内=qU′(U′为内阻上的电势降);在外电路部分,电流做功W外=qU(U为路端电压),电能转化成其它形式的能。可见,整个电路中的能量循环转化,电源产生多少电能,电路就消耗多少,收支平衡。即:W非=W内+W外或qE=qU′+qU
对于一个闭合电路,它的能量应该是守恒的,但又在不同形式间转化,通过做功方式完成。在电源部分,非静电力做正功W非=qE,将其它形式的能转化成电能。而内阻上电流做功,将电能转化成内能W内=qU′(U′为内阻上的电势降);在外电路部分,电流做功W外=qU(U为路端电压),电能转化成其它形式的能。可见,整个电路中的能量循环转化,电源产生多少电能,电路就消耗多少,收支平衡。即:W非=W内+W外或qE=qU′+qU
(2)电功与电热
如图所示,用电器两端电压U,电流I。时间t内,电流对用电器做功W=UIt;该用电器的电功率P=W/t=UI;若用电器电阻为R,时间t内该用电器产生的热量Q=I2Rt(焦耳定律);该用电器的热功率P热=Q/t=I2R。
①若电路为纯电阻电路,电功等于电热:W=Q=UIt=I
2R t=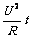 。
。
②若电路为非纯电阻电路(如电动机和电解槽),由于电能除了转化为电热以外还同时转化为机械能或化学能等其它能,所以电功必然大于电热:W>Q,这时电功只能用W=UIt计算,电热只能用Q=I 2Rt计算,两式不能通用。
电功就是电场力做的功,因此是W=UIt;由焦耳定律,电热Q=I2Rt。其微观解释是:电流通过金属导体时,自由电子在加速运动过程中频繁与正离子相碰,使离子的热运动加剧,而电子速率减小,可以认为自由电子只以某一速率定向移动,电能没有转化为电子的动能,只转化为内能。
[例题3]如图所示的电路中,电源电动势E=6V,内电阻r=1Ω,M为一小电动机,其内部线圈的导线电阻RM=2Ω。R为一只保护电阻,R=3Ω。电动机正常运转时,电压表的示数为0.3V,求电动机得到的电功率和它转动的机械功率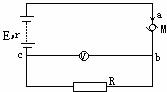 。
。
本题的关键是电路中有电动机,不是纯电阻电路,因而欧姆定律不再适用。突破点是利用电压表与R的阻值,求出电路中的电流,再求出各部分的电压和功率。
解:由部分电路欧姆定律知:电路中电流I=Ubc/R=0.3/3=0.1A
由闭合电路欧姆定律知:Uab=E-Ir-Ubc=6V-0.1×1V-0.3V=5.6V
所以电动机得到的功率为电流对它做功的功率:P电=UabI=5.6×0.1W=0.56W
解答完毕后,可再让学生求一下电动机的效率η以加深非电阻电路P电≠P热的印象。P电转化为两部分:机械功率和电机导线内阻上的发热功率,电动机转化的机械功率为:P机=P电-I2RM=0.56W-0.12×2W=0.54W
[例题4]某一电动机,当电压U1=10V时带不动负载,因此不转动,这时电流为I1=2A。当电压为U2=36V时能带动负载正常运转,这时电流为I2=1A。求这时电动机的机械功率是多大?
解:电动机不转时可视为为纯电阻,由欧姆定律得,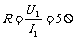 ,这个电阻可认为是不变的。电动机正常转动时,输入的电功率为
,这个电阻可认为是不变的。电动机正常转动时,输入的电功率为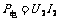 =36W,内部消耗的热功率
=36W,内部消耗的热功率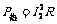 =5W,所以机械功率P=31W
=5W,所以机械功率P=31W
由这道例题可知:电动机在启动时电流较大,容易被烧坏;正常运转时电流反而较小。
[例题5]如图所示,A、B两灯泡额定电压都为110V,额定功率PA=100W,PB=40W,接在220V电路上。欲使灯泡正常发光,且电路中消耗的功率最少,用以下哪种接法?

解:A图中,由R=U2/P知,两灯上电压不能同时达到110V,故不可能都正常发光,A被排除。
B图中,由R=U2/P知RA<RB,当RA与变阻器R并联后,该部分电阻更小,不可能与B同时正常发光,所以B被排除。
C图中,想让A、B都正常发光,则两个电灯上电压都应为110V,即A与B和R并联后的阻值相同,则A的功率与并联部分的功率相同,总功率为2PA=200W。同理,D图中,R上分压与A、B并联部分相同,则两部分电阻与电功率相同,所以总功率为2(PA+PB)=280W。选项C正确。
非纯电阻电路中,电流做功也不再只转化为内能,而是根据具体情况转化为其它各种形式的能。
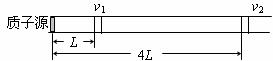 [例题6]来自质子源的质子(初速度为零),经一加速电压为800kV的直线加速器加速,形成电流强度为1mA的细柱形质子流。已知质子电荷e=1.60×10-19C。这束质子流每秒打到靶上的质子数为_________。假定分布在质子源到靶之间的加速电场是均匀的,在质子束中与质子源相距L和4L的两处,各取一段极短的相等长度的质子流,其中的质子数分别为n1和n2,则n1∶n2=_______。
[例题6]来自质子源的质子(初速度为零),经一加速电压为800kV的直线加速器加速,形成电流强度为1mA的细柱形质子流。已知质子电荷e=1.60×10-19C。这束质子流每秒打到靶上的质子数为_________。假定分布在质子源到靶之间的加速电场是均匀的,在质子束中与质子源相距L和4L的两处,各取一段极短的相等长度的质子流,其中的质子数分别为n1和n2,则n1∶n2=_______。
解:按定义,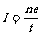 ,∴
,∴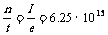 。
。
由于各处电流相同,设这段长度为l,其中的质子数为n个,则由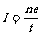 和
和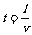 得
得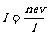 ,∴
,∴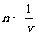 。而
。而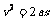 ,∴
,∴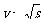 ,∴
,∴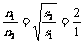 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com