
25. 解排列组合问题有哪些规律?
答:解排列组合问题的规律是:相邻问题捆绑法;不邻问题插空法;多排问题单排法;定位问题优先法;多元问题分类法;有序分配问题法;选取问题先排后排法;至多至少问题间接法.
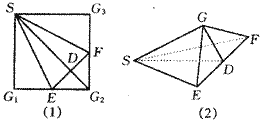
23.设a、b是平面α外的任意两条线段,a、b相等能否推出它们在α内的射影相等?反过来呢? 答:设长度为d的线段所在直线与平面α所成的角为θ,其射影的长度为d′,那么d′=d·cosθ.因此,决定射影的长度的因素除了线段的长度d外,还有直线和平面所成的角. 当a=b,但a、b与平面α所成的角θ1、θ2不相等时,a、b在平面内的射影a′、b′不一定相等. 反过来,当a、b在平面内的射影a′、b′相等,但a、b与平面α所成的角θ1、θ2不相等时,a、b也不一定相等. 24.怎样通过“折叠问题”来提高空间想象能力和巩固他们相关的立体几何知识? 答:一般地说,这里的问题常常是把一个已知的平面图形折叠成一个立体图形(相反的问题是“展平问题”,即把一个已知的立体图形展平成一个平面图形).这就要求学生认清平面图形中各已知条件的相互关系及其本质,并且在把这一平面图形折叠成立体图形以后,能分清已知条件中有哪些发生了变化,哪些未发生变化.这些未变化的已知条件都是学生分析问题和解决问题的依据. 例如选择题:如图2(1),在正方形SG1G2G3中,E,F分别是G1G2及G2G3的中点,D是EF的中点,现在沿SE,SF及EF把这个正方形折成一个由四个三角形围成的“四面体”,使G1,G2,G3三点重合,重合后的点记为G(图2(2)),那么在四面体S-EFG中必有( ).
 |
|
图2 |
A.SG⊥△EFG所在平面 B.SD⊥△EFG所在平面 C.GF⊥△SEF所在平面 D.GD⊥△SEF所在平面 这道题虽然涉及“四面体”的概念,实际上主要是用来巩固直线和平面垂直的判定定理和培养学生的空间想象能力.已知的是一个正方形,那么SG1⊥G1E,EG2⊥G2F,FG3⊥G3S,这些条件在折叠后仍然不变.这一点应是学生解决这一问题的主要思路. 根据这一点,可以看出,折叠后得到的四面体S-EFG中,一定有SG⊥GE,且SG⊥GF,即SG⊥△EFG所在平面.于是应该选A.
18.证明不等式可以运用哪些常用的数学方法?
答:(1)分析法.从要证明的不等式出发,寻找使这个不等式成立的某一充分条件,如此逐步往前追溯(执果索因),一直追溯到已知条件或一些真命题为止.例如要证a2+b2≥2ab,我们通过分析知道,a2+b2≥2ab的某一充分条件是a2-2ab+b2≥0,即(a-b)2≥0,因此只要证明(a-b)2≥0就行了.由于(a-b)2≥0是真命题,所以a2+b2≥2ab成立.分析法的证明过程表现为一连串的“要证……只要证……”,最后推至已知条件或真命题.
(2)综合法.从已知(已经成立)的不等式或定理出发,逐步推出(由因导果)所证的不等式成立.例如要证a2+b2≥2ab,我们从(a-b)2≥0,得a2-2ab+b2≥0,移项得a2+b2≥2ab.综合法的证明过程表现为一连串的“因为……所以……”,可用一连串的“ ”来代替.
综合法的证明过程是分析法的思考过程的逆推,而分析法的证明过程恰恰是综合法的思考过程.当我们不易找到作为出发点的不等式来证明结论时,通常改用分析法来证明.
(3)比较法.根据a>b与a-b>0等价,所以要证甲式大于乙式,只要证明甲式减去乙式所得的差式在两式中的字母的可取值范围内取正值就可以了.这就是比差法.还有一种比较法是比商法,例如已知甲式、乙式在其中字母的可取值范围内均取正值,那么要证甲式大于乙式,只要证明甲式除以乙式所得的商式在这一字母取值范围内均取大于1的值就可以了.比商法较为复杂,使用时务必注意字母的取值范围.
(4)逆证法.这是分析法的一种特殊情况,即从要证明的等式出发,寻找使这个不等式成立的充要条件,如此逐步往前追溯,一直追溯到已知条件或一些真命题为止.逆证法的证明过程表现为一连串的“即”,可用一连串的“?”来代替,最后推至已知条件或真命题.
(5)放缩法.这也是分析法的一种特殊情况,它的根据是不等式关系的传递性--a≤b,b≤c,则a≤c,所以要证a≤c,只要证明“大于或等于a”的b≤c就行了.
”来代替.
综合法的证明过程是分析法的思考过程的逆推,而分析法的证明过程恰恰是综合法的思考过程.当我们不易找到作为出发点的不等式来证明结论时,通常改用分析法来证明.
(3)比较法.根据a>b与a-b>0等价,所以要证甲式大于乙式,只要证明甲式减去乙式所得的差式在两式中的字母的可取值范围内取正值就可以了.这就是比差法.还有一种比较法是比商法,例如已知甲式、乙式在其中字母的可取值范围内均取正值,那么要证甲式大于乙式,只要证明甲式除以乙式所得的商式在这一字母取值范围内均取大于1的值就可以了.比商法较为复杂,使用时务必注意字母的取值范围.
(4)逆证法.这是分析法的一种特殊情况,即从要证明的等式出发,寻找使这个不等式成立的充要条件,如此逐步往前追溯,一直追溯到已知条件或一些真命题为止.逆证法的证明过程表现为一连串的“即”,可用一连串的“?”来代替,最后推至已知条件或真命题.
(5)放缩法.这也是分析法的一种特殊情况,它的根据是不等式关系的传递性--a≤b,b≤c,则a≤c,所以要证a≤c,只要证明“大于或等于a”的b≤c就行了.
(6)反证法.先假定要证的不等式的反面成立,然后推出与已知条件(或已知的真命题)相矛盾的结论,从而断定反证假定是错误的.因而要证的不等式一定成立. (7)穷举法.对要证的不等式按已知条件分成各种情况一一加以证明(防止重复或遗漏某一可能情况). 要注意:在证明不等式时,应灵活运用上述方法,并通过运用多种方法来提高他们的思维能力. 19.怎样教讨论曲线的性质? 答:在中学里,除了直线这种简单的情况外,对于较为简单的曲线,讨论其几何性质一般包括以下四个方面: (1)确定曲线的范围.由曲线方程F(x,y)=0分别确定变量x与y的取值范围,从而分别判断曲线的左、右与上、下部分的“顶点”的分布情况. (2)判断有没有对称性.在曲线方程F(x,y)=0中,如果把x(或y)换成-x(或-y),方程不变,那么曲线关于y(或x)轴对称;如果把x与y同时换成-x与-y,方程不变,那么曲线关于原点对称(这时曲线关于x轴或y轴却不一定对称). (3)求出在x轴上的“截距”(即求出曲线与x轴的交点的横坐标)和y轴上的“截距”(即求出曲线与y轴的交点的纵坐标).这可以通过解由F(x,y)=0与y=0(或x=0)所组成的方程组求得.注意曲线与坐标轴的交点不一定是曲线的“顶点”. (4)判断有没有渐近线.对于椭圆、双曲线、抛物线等圆锥曲线,还要研究它的离心率在数值上有什么特征,等等. 20.求轨迹方程的基本方法是什么? 答:轨迹是动点按照一定的规律即轨迹条件运动而形成的,这个轨迹条件一旦用动点坐标的数学表达式表示出来,轨迹方程就产生了.因此,求轨迹方程的基本方法是(图1)
 |
|
图1 |
这里所谓的“坐标化”,就是把轨迹条件中的各个数、量用动点坐标表示出来.轨迹条件可以表现为不同的形式,其中使它转化为有利于坐标化的形式正是困难所在. 21.关于直线和圆锥曲线的关系,主要有哪些问题? 答:(1)直线和圆锥曲线位置关系的制定; (2)切线方程及与相切有关的问题; (3)弦长及与弦长有关的问题; (4)弦的中点及与此有关的问题; (5)曲线关于直线对称的问题. 22.在解决与圆锥曲线有关的问题时,怎样帮助学生运用函数的思想? 答:不少与圆锥曲线有关的问题中的各个数量在运动变化时,都是相互联系、相互制约的,它们之间构成函数关系.这类问题若用函数思想来分析、寻找解题思路,会有很好的效果.
17. 在用反三角函数表示直线的倾斜角、两条异面直线所成的角等时,你是否注意到它们各自的取值范围及意义?
①异面直线所成的角、直线与平面所成的角、向量的夹角的取值范围依次是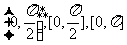 .
.
②直线的倾斜角、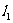 到
到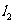 的角、
的角、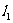 与
与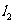 的夹角的取值范围依次是
的夹角的取值范围依次是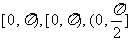 .
.
③反正弦、反余弦、反正切函数的取植范围分别是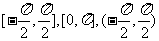
11.求一个数列的通项公式时,有哪些基本方法? 答:有以下四种基本方法: (1)直接法.就是由已知数列的项直接写出,或通过对已知数列的项进行代数运算写出. (2)观察分析法.根据数列构成的规律,观察数列的各项与它所对应的项数之间的内在联系,经过适当变形,进而写出第n项an的表达式即通项公式. (3)待定系数法.求通项公式的问题,就是当n=1,2,…时求f(n),使f(n)依次等于a1,a2,…的问题.因此我们可以先设出第n项an关于变数n的表达式,再分别令n=1,2,…,并取an分别等于a1,a2,…,然后通过解方程组确定待定系数的值,从而得出符合条件的通项公式. (4)递推归纳法.根据已知数列的初始条件及递推公式,归纳出通项公式. 12.等差数列有哪些基本性质? 答:(1)当d>0时,等差数列中的数随项数的增大而增大;当d<0时,等差数列中的数随项数的减小而减小;当d=0时,等差数列中的数等于一个常数.注意:不能说等差数列或它的通项公式是一次函数,等差数列只是某个一次函数的一系列孤立的函数值;一次函数是有严格定义的,它的定义域是实数集R,图象是(连续的)一条直线.这是目前教学中普遍出错的地方! (2)在有穷的等差数列中,与首末两项等距离的两项的和都相等,且等于首末两项的和. (3)如果m+n=p+q(m,n,p,q都是正整数,那么am+an=ap+aq)。 (4)如果等差数列的各项都加上一个相同的数,那么所得的数列仍是等差数列,且公差不变. (5)两个等差数列各对应项的和组成的数列仍是等差数列,且公差等于这两个数列的公差的和. 13.等比数列有哪些基本性质? 答:(1)当q>1时,如果存在一项a>0(或<0),那么等比数列中的数随项数的增大而增大(或减小);当0<q<1时,如果存在一项a>0(或<0),那么等比数列中的数随项数的增大而减小(或增大);当q=1时,等比数列中的数等于同一个常数;当q<0时,等比数列中的数不具有单调性. (2)在有穷的等比数列中,与首末两项等距离的两项的积都相等,且等于首末两项的积. (3)如果m+n=p+q(m,n,p,q都是正整数),那么am·an=ap·aq. (4)如果数列{an}是等比数列,那么它所有的项都不等于0,且所有的an·an+2>0. (5)如果数列{an}是等比数列,那么数列{can}(c为常数),{an-1},{|an|}也都是等比数列,且其中{can}的公比不变,{an-1}的公比等于原公比的倒数,{|an|}的公比等于原公比的绝对值. (6)两个等比数列各对应项的积组成的数列仍是等比数列,且公比等于这两个数列的公比的积. 14.为什么当λ,μ为实数时,有λ(μa)=μ(λa)=(λμ)a? 答:这是因为由实数与向量的积的定义可知,向量λ(μa),μ(λa),(λμ)a是互相平行的向量,它们的方向也相同,且 |λ(μa)|=|μ(λa)|=|(λμ)a|=|λμ|·|a|, 所以λ(μa)=μ(λa)=(λμ)a(=(μλ)a). 这个运算律叫做向量数乘的结合律. 15平面向量基本定理的实质是什么? 答:平面向量基本定理指出:如果e1,e2是同一平面内的两个不共线向量,那么对这一平面内的任一向量a,有且只有一对实数λ1,λ2,使a=λ1e1+λ2e2. 这个定理告诉我们,平面内任一向量都可以沿两个不共线的方向分解为两个向量的和,并且这种分解是惟一的. λe1+λe2叫做e1,e2的一个线性组合.由平面向量基本定理可知,如果e1,e2不共线,那么由e1,e2的所有线性组合构成的集合{λ1e1+λ2e2|λ1,λ2∈R}就是平面内的全体向量.所以,我们把e1,e2(最好写成{e1,e2},注意花括弧中e1,e2之间必须用逗号)叫做这一平面内所有向量的一组基底,并把基底中的向量叫做基向量. 向量的合成与分解在物理学和工程技术中有着广泛的应用. 16.怎样归纳确定三角形形状的思路? 答:我们知道,三角形的形状,以角的大小为标准,可以确定其中的锐角三角形、直角三角形、钝角三角形;以边长的关系为标准,可以确定其中的等腰三角形、等边三角形、直角三角形(包括等腰直角三角形).用三角知识确定三角形形状的思路如下表所示:
|
三角形形状 |
确定三角形形状的思路 |
|
锐角三角形(如C为锐角) |
cosC>0,或tanC>0;或a2+b2>c2 |
|
直角三角形(如C为直角) |
cosC=0,或sinC=1;或a2+b2=c2 |
|
钝角三角形(如C为钝角) |
cosC<0,或tanC<0;或a2+b2<c2 |
|
等腰三角形(如边b,c) |
B=C;或b=c |
|
等边三角形 |
A=B=C;或a=b=c |
10.函数的一些重要性质,如何区别?
①如果函数 对于一切
对于一切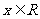 ,都有
,都有 ,那么函数
,那么函数 的图象关于直线
的图象关于直线 对称.
对称.
②函数 与函数
与函数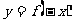 的图象关于直线
的图象关于直线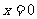 对称;
对称;
函数 与函数
与函数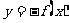 的图象关于直线
的图象关于直线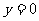 对称;
对称;
函数 与函数
与函数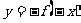 的图象关于坐标原点对称.
的图象关于坐标原点对称.
③函数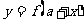 与函数
与函数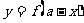 的图象关于直线
的图象关于直线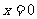 对称.
对称.
④若奇函数 在区间
在区间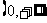 上是递增函数,则
上是递增函数,则 在区间
在区间 上也是递增函数.
上也是递增函数.
⑤若偶函数 在区间
在区间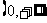 上是递增函数,则
上是递增函数,则 在区间
在区间 上是递减函数.
上是递减函数.
⑥函数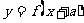
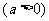 的图象是把函数
的图象是把函数 的图象沿x轴向左平移a个单位得到的;
的图象沿x轴向左平移a个单位得到的;
函数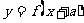 (
(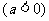 的图象是把函数
的图象是把函数 的图象沿x轴向右平移
的图象沿x轴向右平移
 个单位得到的;
个单位得到的;
函数 +a
+a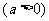 的图象是把函数
的图象是把函数 助图象沿y轴向上平移a个单位得到的;
助图象沿y轴向上平移a个单位得到的;
函数 +a
+a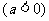 的图象是把函数
的图象是把函数 助图象沿y轴向下平移
助图象沿y轴向下平移 个单位得到的.
个单位得到的.
⑦函数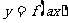
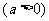 的图象是把函数
的图象是把函数 的图象沿x轴伸缩为原来的
的图象沿x轴伸缩为原来的 得到的;
得到的;
函数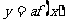
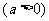 的图象是把函数
的图象是把函数 的图象沿y轴伸缩为原来的a倍得到的.
的图象沿y轴伸缩为原来的a倍得到的.
1.什么是数学方法?中学数学有哪些常用的基本数学方法?
答:所谓方法,是指人们为了达到某种目的而采取的手段、途径和行为方式中所包含的可操作的规则或模式.人们通过长期的实践,发现了许多运用数学思想的手段、门路或程序.同一手段、门路或程序被重复运用了多次,并且都达到了预期的目的,就成为数学方法.数学方法是以数学的工具进行科学研究的方法,即用数学语言表达事物的状态、关系和过程,经过推导、运算与分析,以形成解释、判断和预言的方法.
数学方法具有以下三个基本特征:一是高度的抽象性和概括性,二是逻辑的严密性及结论的确定性,三是应用的普遍性和可操作性.
数学方法在科学技术研究中具有举足轻重的地位和作用:一是提供简洁确定的形式化语言,二是提供数量分析及计算的方法,三是提供逻辑推理的工具.现代科学技术特别是电子计算机的发展,与数学方法的地位和作用的强化正好是相辅相成.
在中学数学中经常用到的基本数学方法,大致可以分为以下三类:
(1)逻辑学中的方法.例如分析法(包括逆证法)、综合法、反证法、归纳法、穷举法(要求分类讨论)等.这些方法既要遵重逻辑学中的基本规律和法则,又因为运用于数学之中而具有数学的特色.
(2)数学中的一般方法.例如建模法、消元法、降次法、代入法、图象法(也称坐标法,在代数中常称图象法,在学生今后要学习的解析几何中常称坐标法)、比较法(数学中主要是指比较大小,这与逻辑学中的多方位比较不同)等.这些方法极为重要,应用也很广泛.
(3)数学中的特殊方法.例如配方法、待定系数法、加减法、公式法、换元法(也称之为中间变量法)、拆项补项法(含有添加辅助元素实现化归的数学思想)、因式分解诸方法,以及平行移动法、翻折法等.这些方法在解决某些数学问题时也起着重要作用,对于某一类问题也都是一种通法.
2.解不等式时,常用的等价转化有哪些情况?
答:设y1和y2都是x的函数,那么下列各不等式等价:
(1) │y1│≤y2(y2≥0) -y2≤y1≤y2,
│y1│>y2(y2≥0)
-y2≤y1≤y2,
│y1│>y2(y2≥0) y1<-y2或y1>y2;
(2) │y1│≤c(c≥0)
y1<-y2或y1>y2;
(2) │y1│≤c(c≥0) y12≤c2,
│y1│>c(c≥0)
y12≤c2,
│y1│>c(c≥0) y12>c2;
(3) y1·y2≥0
y12>c2;
(3) y1·y2≥0 y1≥0且y2≥0,或y1≤0且y2≤0,
y1·y2<0
y1≥0且y2≥0,或y1≤0且y2≤0,
y1·y2<0 y1>0且y2<0,或y1<0且y2>0;
(4) y1/y2>0(y2≠0)
y1>0且y2<0,或y1<0且y2>0;
(4) y1/y2>0(y2≠0) y1·y2>0,
y1/y2<0(y2≠0)
y1·y2>0,
y1/y2<0(y2≠0) y1·y2<0.
3.怎样正确理解逻辑联结词“或”的意义?
答:“或”这个逻辑联结词的用法,一般有两种解释:一是“不可兼有”,即“a或b”是指a,b中的某一个,但不是两者.日常生活中有时采用这一解释.例如“你去或我去”,人们在理解上不会认为有你我都去这种可能.另一是“可兼有”,即“a或b”是指a,b中的任何一个或两者.例如“x∈A或x∈B”,是指x可能属于A但不属于B(“但”在这里实际上等价于另一逻辑联结词“且”),x也可能不属于A但属于B,x还可能既属于A又属于B(即x∈A∩B).又如在“p真或q真”中,可能只有p真,也可能只有q真,还可能p,q都为真.数学书籍中一般采用后一种解释,运用数学语言和解数学选择题时,都要遵守这一点,还要注意“可兼有”并不意味“一定兼有”.
4. “p或q”“p且q”“非p”这三个复合命题概念后,怎样进行真假概括?
答:(1)对于复合命题“p或q”,当且仅当p,q中至少有一个为真(包括两个同时为真)时,它是真命题;当且仅当p,q都为假时,它是假命题
(2)对于复合命题“p且q”,当且仅当p,q都为真时,它是真命题;当且仅当p,q中至少有一个为假(包括两个同时为假)时,它是假命题.
(3)对于复合命题“非p”,当且仅当p为真时,它是假命题;当且仅当p为假时,它是真命题.
以上也可以利用真值表示进行概括.
可以看出,要使学生正确理解上述概念,还要让他们熟练掌握并会灵活运用“至少”“最多”“同时”,以及“至少有一个是(不是)”“最多有一个是(不是)”“都是(不是)”“不都是”这些词语.这也是学习数学的难点之一,需要长期不懈地进行训练,才能达到要求.
5.怎样理解四种命题?怎样利用反证法来理解四种命题的关系?
答:学生在初中未学过否命题和逆否命题.可以举例来说.
命题甲:如果∠1、∠2是对顶角,那么∠1=∠2.
命题乙:如果∠1=∠2,那么∠1、∠2是对顶角.
命题丙:如果∠1、∠2不是对顶角,那么∠1≠∠2.
命题丁:如果∠1≠∠2,那么∠1、∠2不是对顶角.
这里命题甲、乙互为逆命题;命题丙是把命题甲的条件、结论都加以否定后得到的,所以我们把命题丙叫做命题甲的否命题(注意让学生把“否命题”一词与刚学过的逻辑联结词“非”的使用区别开来,“非”通常只否定结论),并且命题甲、丙互为否命题;命题丁是把命题乙的条件、结论都加以否定后得到的,所以命题乙、丁互为否命题,我们把命题丁叫做命题甲的逆否命题.学生经过仔细分析,可以看出:命题丁也可以通过把命题丙的条件、结论颠倒过来而得到,所以命题丙、丁互为逆命题,我们也可以把命题丁叫做命题甲的否逆命题.命题甲的逆否命题和否逆命题相同,我们一般只用“逆否命题”一词.
利用反证法,很容易证明:在四种命题中,原命题与逆否命题同时成立或同时不成立,逆命题与否命题同时成立或同时不成立(可以让学生就上面的例子试一试).
以上就是所谓“四种命题的关系”.
6.怎样用推出符号对“充分且不必要条件”“必要且不充分条件”和“充要条件”进行概括?
答:(1)若p
y1·y2<0.
3.怎样正确理解逻辑联结词“或”的意义?
答:“或”这个逻辑联结词的用法,一般有两种解释:一是“不可兼有”,即“a或b”是指a,b中的某一个,但不是两者.日常生活中有时采用这一解释.例如“你去或我去”,人们在理解上不会认为有你我都去这种可能.另一是“可兼有”,即“a或b”是指a,b中的任何一个或两者.例如“x∈A或x∈B”,是指x可能属于A但不属于B(“但”在这里实际上等价于另一逻辑联结词“且”),x也可能不属于A但属于B,x还可能既属于A又属于B(即x∈A∩B).又如在“p真或q真”中,可能只有p真,也可能只有q真,还可能p,q都为真.数学书籍中一般采用后一种解释,运用数学语言和解数学选择题时,都要遵守这一点,还要注意“可兼有”并不意味“一定兼有”.
4. “p或q”“p且q”“非p”这三个复合命题概念后,怎样进行真假概括?
答:(1)对于复合命题“p或q”,当且仅当p,q中至少有一个为真(包括两个同时为真)时,它是真命题;当且仅当p,q都为假时,它是假命题
(2)对于复合命题“p且q”,当且仅当p,q都为真时,它是真命题;当且仅当p,q中至少有一个为假(包括两个同时为假)时,它是假命题.
(3)对于复合命题“非p”,当且仅当p为真时,它是假命题;当且仅当p为假时,它是真命题.
以上也可以利用真值表示进行概括.
可以看出,要使学生正确理解上述概念,还要让他们熟练掌握并会灵活运用“至少”“最多”“同时”,以及“至少有一个是(不是)”“最多有一个是(不是)”“都是(不是)”“不都是”这些词语.这也是学习数学的难点之一,需要长期不懈地进行训练,才能达到要求.
5.怎样理解四种命题?怎样利用反证法来理解四种命题的关系?
答:学生在初中未学过否命题和逆否命题.可以举例来说.
命题甲:如果∠1、∠2是对顶角,那么∠1=∠2.
命题乙:如果∠1=∠2,那么∠1、∠2是对顶角.
命题丙:如果∠1、∠2不是对顶角,那么∠1≠∠2.
命题丁:如果∠1≠∠2,那么∠1、∠2不是对顶角.
这里命题甲、乙互为逆命题;命题丙是把命题甲的条件、结论都加以否定后得到的,所以我们把命题丙叫做命题甲的否命题(注意让学生把“否命题”一词与刚学过的逻辑联结词“非”的使用区别开来,“非”通常只否定结论),并且命题甲、丙互为否命题;命题丁是把命题乙的条件、结论都加以否定后得到的,所以命题乙、丁互为否命题,我们把命题丁叫做命题甲的逆否命题.学生经过仔细分析,可以看出:命题丁也可以通过把命题丙的条件、结论颠倒过来而得到,所以命题丙、丁互为逆命题,我们也可以把命题丁叫做命题甲的否逆命题.命题甲的逆否命题和否逆命题相同,我们一般只用“逆否命题”一词.
利用反证法,很容易证明:在四种命题中,原命题与逆否命题同时成立或同时不成立,逆命题与否命题同时成立或同时不成立(可以让学生就上面的例子试一试).
以上就是所谓“四种命题的关系”.
6.怎样用推出符号对“充分且不必要条件”“必要且不充分条件”和“充要条件”进行概括?
答:(1)若p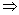 q,且
q,且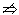 p,则p是q的充分且不必要条件,q是p的必要且不充分条件; (2)若q
p,则p是q的充分且不必要条件,q是p的必要且不充分条件; (2)若q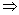 p,且p
p,且p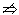 q,则p是q的必要且不充分条件,q是p的充分且不必要条件;
(3)若p
q,则p是q的必要且不充分条件,q是p的充分且不必要条件;
(3)若p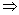 q,且q
q,且q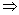 p,则p是q的充要条件(此时q也是p的充要条件);
(4)若p
p,则p是q的充要条件(此时q也是p的充要条件);
(4)若p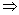 q,且┐p
q,且┐p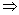 q ┐,则p是q的充要条件(此时q也是p的充要条件).
7.怎样让正确判断“充分且不必要条件”“必要且不充分条件”“充要条件”以及“不充分且不必要条件”?
答:这四种情况反映了条件p和结论q之间的因果关系,所以在判断时应该让学生:
(1)确定条件是什么,结论是什么;
(2)尝试从条件推导结论,从结论推导条件;
(3)确定条件是结论的什么条件.
要证明命题的条件是充要的,就既要证明原命题成立,又要证明它的逆命题成立.证明原命题成立即证明条件的充分性,证明逆命题成立即证明条件的必要性.
8.如何利用已知函数的单调性来判定较复杂函数的单调性?
答:如果函数f(x)、g(x)在区间B上具有单调性,那么在B上:
(1)f(x)与f(x)+c(c为常数)具有相反的单调性.
(2)f(x)与c·f(x)当c>0时具有相同的单调性,当c<0时具有相反的单调性.
(3)当f(x)恒不为0时,f(x)与1/f(x)具有相反的单调性.
(4)当f(x)恒为非负时,f(x)与f(x)具有相反的单调性.
(5)当f(x)、g(x)都是增(减)函数时,f(x)+g(x)也是增(减)函数.
(6)设f(x)、g(x)都是增(减)函数,则f(x)·g(x)当f(x)、g(x)两者都恒大于0时也是增(减)函数,当两者都恒小于0时是减(增)函数.
9.什么叫做函数的奇偶性?
答:一般地,设有函数f(x),对于其定义域内的任意一个x值,如果都有f(-x)=-f(x),那么称f(x)是奇函数;如果都有f(-x)=f(x),那么称f(x)是偶函数.
如果函数f(x)是奇函数或偶函数,那么称f(x)具有奇偶性.
函数的奇偶性也是函数的整体性质之一.这里指出以下几点.
(1)函数的奇偶性是针对函数的定义域讲的.由于任意的x与-x都要在定义域内,所以奇(偶)函数的定义域关于原点对称.我们在判定函数是否具有奇偶性时,应先确定其定义域关于原点是否对称.不对称就没有奇偶性(定义域对称,才能使函数图象关于原点或y轴对称).
(2)既是奇函数又是偶函数的函数,一定有解析式y=f(x)=0,但它的定义域可以各色各样(必须关于原点对称),所以不是惟一的.解析式不为f(x)=0的函数,不可能既是奇函数又是偶函数.
(3)奇(偶)函数还具有以下性质:
--两个奇(偶)函数的和(差)也是奇(偶)函数.
--两个函数的积(商,分母恒不为0),当其奇偶性相同时为偶函数,当其奇偶性相反时为奇函数.
--奇(偶)函数在其定义域内关于原点对称的区间上单调性相同(反).
--偶函数一般不存在反函数;如果一个奇函数有反函数,那么其反函数也是奇函数.
(4)构造奇(偶)函数的简单方法:设f(x)是定义域关于原点对称的函数,则
F1(x)=(1/2)(f(x)+f(-x))
是偶函数,而
F2(x)=(1/2)(f(x)-f(-x))
是奇函数.显然,F1(x)+F2(x)=f(x),所以这样的f(x)总可以表示成一个偶函数与一个奇函数之和.
q ┐,则p是q的充要条件(此时q也是p的充要条件).
7.怎样让正确判断“充分且不必要条件”“必要且不充分条件”“充要条件”以及“不充分且不必要条件”?
答:这四种情况反映了条件p和结论q之间的因果关系,所以在判断时应该让学生:
(1)确定条件是什么,结论是什么;
(2)尝试从条件推导结论,从结论推导条件;
(3)确定条件是结论的什么条件.
要证明命题的条件是充要的,就既要证明原命题成立,又要证明它的逆命题成立.证明原命题成立即证明条件的充分性,证明逆命题成立即证明条件的必要性.
8.如何利用已知函数的单调性来判定较复杂函数的单调性?
答:如果函数f(x)、g(x)在区间B上具有单调性,那么在B上:
(1)f(x)与f(x)+c(c为常数)具有相反的单调性.
(2)f(x)与c·f(x)当c>0时具有相同的单调性,当c<0时具有相反的单调性.
(3)当f(x)恒不为0时,f(x)与1/f(x)具有相反的单调性.
(4)当f(x)恒为非负时,f(x)与f(x)具有相反的单调性.
(5)当f(x)、g(x)都是增(减)函数时,f(x)+g(x)也是增(减)函数.
(6)设f(x)、g(x)都是增(减)函数,则f(x)·g(x)当f(x)、g(x)两者都恒大于0时也是增(减)函数,当两者都恒小于0时是减(增)函数.
9.什么叫做函数的奇偶性?
答:一般地,设有函数f(x),对于其定义域内的任意一个x值,如果都有f(-x)=-f(x),那么称f(x)是奇函数;如果都有f(-x)=f(x),那么称f(x)是偶函数.
如果函数f(x)是奇函数或偶函数,那么称f(x)具有奇偶性.
函数的奇偶性也是函数的整体性质之一.这里指出以下几点.
(1)函数的奇偶性是针对函数的定义域讲的.由于任意的x与-x都要在定义域内,所以奇(偶)函数的定义域关于原点对称.我们在判定函数是否具有奇偶性时,应先确定其定义域关于原点是否对称.不对称就没有奇偶性(定义域对称,才能使函数图象关于原点或y轴对称).
(2)既是奇函数又是偶函数的函数,一定有解析式y=f(x)=0,但它的定义域可以各色各样(必须关于原点对称),所以不是惟一的.解析式不为f(x)=0的函数,不可能既是奇函数又是偶函数.
(3)奇(偶)函数还具有以下性质:
--两个奇(偶)函数的和(差)也是奇(偶)函数.
--两个函数的积(商,分母恒不为0),当其奇偶性相同时为偶函数,当其奇偶性相反时为奇函数.
--奇(偶)函数在其定义域内关于原点对称的区间上单调性相同(反).
--偶函数一般不存在反函数;如果一个奇函数有反函数,那么其反函数也是奇函数.
(4)构造奇(偶)函数的简单方法:设f(x)是定义域关于原点对称的函数,则
F1(x)=(1/2)(f(x)+f(-x))
是偶函数,而
F2(x)=(1/2)(f(x)-f(-x))
是奇函数.显然,F1(x)+F2(x)=f(x),所以这样的f(x)总可以表示成一个偶函数与一个奇函数之和.
80. ---You are so lucky. ---What do you mean ____that? (2002年春招)
A. for B. in C. of D. by
语法复习十七:介 词
1~5 ABCDA 6~10 BCDBC 11~15 DBABC 16~20 BACBC 21~25 DABCD 26~30 ABCDA 31~35 BCDAB 36~40 ADDCC 41~45 ADBDB 46~50 CCACC 51~55 DDDBC 56~60 DCCBB 61~65 BCACB 66~70 DAACD 71~75 CDCAB 76~80 ACCCD
79. I know nothing about the young lady ___she is from Beijing.
A. except B. except for C. except that D. besides (2000 上海高考13)
78. Does John know any other foreign language ___French?
A. except B. but C. besides D. beside ('89MET. 13)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com