
1.P是长方体AC1上底面A1C1内任一点,设AP与三条棱AA1、AB、AD所成的角为α、β、γ,则cos2α+cos2β+cos2γ的值是 ( )
A.1 B.2 C.  D.不确定
D.不确定
4.要正确地区别球面上两点间的直线距离与球面距离.搞清纬度、经度、纬度差、经度差等概念.
同步练习 9.6棱柱、棱锥和球
[选择题]
3.球的概念和性质以及面积、体积是解决有关问题的重要依据;它的轴截面是解决问题的重要“场所”,球半径、截面圆半径、圆心距都在这个图形内,它把空间问题转化为平面问题.
2.三棱锥的等(体)积变换是解决点到面的距离的常见方法之一; “割”“补”是解决立体几何,尤其是体积问题的常用技巧.
正棱锥的四个“特征”直角三角形,是将“空间问题”转化为“平面问题”的桥梁.
1.棱柱、棱锥的概念和性质是研究解决问题的依据,要能正确利用这些知识进行图中点、线、面的位置关系的分析和计算;
[例1]如图,设三棱锥S-ABC的三个侧棱与底面ABC所成的角都是60°,又∠BAC=60°,且SA⊥BC.

(1)求证:S-ABC为正三棱锥;
(2)已知SA=a,求S-ABC的全面积.
证明(1):正棱锥的定义中,底面是正多边形;顶点在底面上的射影是底面的中心,两个条件缺一不可.作三棱锥S-ABC的高SO,O为垂足,连结AO并延长交BC于D.
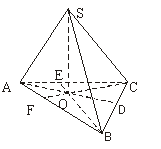
因为SA⊥BC,所以AD⊥BC.又侧棱与底面所成的角都相等,从而O为△ABC的外心,OD为BC的垂直平分线,所以AB=AC.又∠BAC=60°,故△ABC为正三角形,且O为其中心.所以S-ABC为正三棱锥.
解(2):在Rt△SAO中,由于SA=a,∠SAO=600,
所以SO= a,AO=
a,AO= a.因O为重心,
a.因O为重心,
所以AD=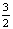 AO=
AO= a,BC=2BD=2ADcot600=
a,BC=2BD=2ADcot600= a,
a,
OD= AD=
AD= a.
a.
在Rt△SOD中,SD2=SO2+OD2=( a)2+(
a)2+( a)2=
a)2= ,则SD=
,则SD= a.于是,(SS-ABC)全=
a.于是,(SS-ABC)全= ·(
·( a)2sin60°+3·
a)2sin60°+3· ·
· a·
a· a=
a= a2.
a2.
◆思悟探讨
(1)求正棱锥的侧面积或全面积还可以利用公式
S正棱锥底=cosα·S正棱锥侧(α为侧面与底面所成的二面角).
(2)注意到高SO= a,底面边长BC=
a,底面边长BC= a是相等的,因此这类正三棱锥还有高与底面边长相等的性质,反之亦真.
a是相等的,因此这类正三棱锥还有高与底面边长相等的性质,反之亦真.
(3)正三棱锥中,若侧棱与底面边长相等,则可称为正四面体,因此正四面体是特殊的正三棱锥,但正三棱锥不一定是正四面体.
[例2] 三棱锥A-BCD的两条棱AB=CD=6,其余各棱长均为5,求三棱锥的内切球半径.

解法一:易知内切球球心O到各面的距离相等.
设E、F为CD、AB的中点,则O在EF上且O为EF的中点.
在△ABE中,AB=6,AE=BE=4,OH= .
.
解法二:设球心O到各面的距离为R.
则4× S
S ×R=VA-BCD,
×R=VA-BCD,
∵S =
= ×6×4=12,VA-BCD=2VC-ABE=6
×6×4=12,VA-BCD=2VC-ABE=6 .
.
∴4× ×12R=6
×12R=6 .∴R=
.∴R= .
.
评述:正多面体与球的切接问题常借助体积求解.
[例3].(2006邯郸一模)已知,三棱柱ABC-A1B1C1中,侧棱与底面成600的角,AB⊥AC,BC1⊥A1C1,AB=4,AC=3.
(1).求证:截面ABC1⊥底面ABC;
(2).求三棱柱ABC-A1B1C1的体积的最小值;
(3).求三棱柱ABC-A1B1C1体积最小时,截面A1BC1与底面ABC所成二面角的大小.


证(1):在三棱柱ABC-A1B1C1 中, AC ∥A1C1,
∵BC1⊥A1C1, ∴BC1⊥AC,又 AB⊥AC,
∴AC⊥面ABC1, ∴面ABC1⊥面ABC.
解(2):作C1H⊥面ABC于H, 则H在AB上,连CH,则∠HCC1=600 当H与A重合时CH最短,棱柱的高C1H=CHtan600= CH最短
CH最短
三棱柱ABC-A1B1C1 的体积V最小.此时,
∠ACC1=600, C1H=AC1=3
V=

解(3)设面ABC交面A1BC1于直线 m,则 m为二面角的棱.
∵AC∥A1C1 , ∴AC∥面A1BC1, AC∥m ,
∴ AB⊥m, 又AC1⊥面ABC,
由三垂线定理知C1B⊥m,
∴∠ABC1为所求二面角的平面角.在RtΔABC1中, tan∠ABC1=

[例4]如图,三个12×12 cm的正方形,都被连结相邻两边中点的直线分成A、B两片(如图(1)),把6片粘在一个正六边形的外面(如图(2)),然后折成多面体(如图(3)),求此多面体的体积.


解法一: 补成一个正方体,如图甲,
V= V正方体=
V正方体= ×123=864 cm3.
×123=864 cm3.

甲 乙
解法二:补成一个三棱锥,如图乙,
V=V大三棱锥-3V小三棱锥=864 cm3.
解法三:如图(3)7设C是所在棱的中点,截面CDE把几何体截成两部分,沿DE把上部分翻转过来可拼成正方体的下一半.
◆思考讨论
补形的方法可将不规则的几何体转化成规则的几何体,这是求多面体体积的常用方法.
5. 补上一个相同的棱柱成为平行六面体;或割成三个相同的三棱锥.
4.先确定点P、A、B、C所在的球面及其直径.
1.提示:BC1在上底面的射影垂直于AC,必为AB.
法二:AC⊥平面ABC1,从而平面ABC1⊥平面ABC……
5.  dS; 6 arccos
dS; 6 arccos ; 7.
; 7. 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com