2．掌握用图象求解不等式的方法．

学习难点

　　 图象法求解不等式中自变量取值范围的确定．

预习问题

　　 我们来看下面两个问题有什么关系？

1．理解一元一次不等式与一次函数的转化关系及本质联系．

2．解关于x的不等式kx+b>mx+n可以转化为：

　　 (1)当自变量x取何值时，直线y=(k-m)x+b-n上的点在x轴的上方．

　　 或(2)求当x取何值时，直线y=kx+b上的点在直线y=mx+n上相应的点的上方．(不等号为“<”时是同样的道理)

学习重点

1．解一元一次不等式可以看作是:当一次函数值大于(或小于)0时，求自变量相应的取值范围．

11.3.2 一次函数与一元一次不等式

学习目标

5．5.10cm

2．略　 3．5.015cm　 4．41.12mm

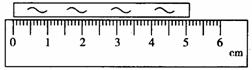
5．如图所示为测量一金属筒时刻度尺示数的示意图，该金属筒长度为　 　　　cm.

答案：1．△x=(12.6-12. 4) mm= 0. 2 mm；

η=△x / x₀ =1. 6%

4．用游标为50分度的卡尺测量某圆柱的直径时，卡尺上的示数如图9所示,可读出圆柱的直径为

　　　　 　mm

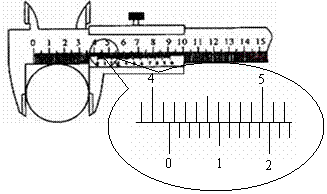
3．读出如图所示游标尺的读数．