
3. 设A=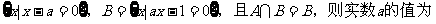 ( )
( )
A. 1 B.  C.
C.
 D.
D.

2. 若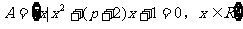 ,且
,且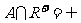 ,则实数中的取值范围是( )
,则实数中的取值范围是( )
A.  B.
B.

C. 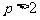 D.
D.

1. 若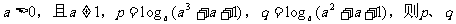 的大小关系为( )
的大小关系为( )
A. 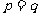 B.
B.
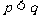

C. 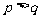 D.
D.
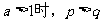 ;
;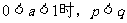

[模拟试题]
分类讨论是一种重要的数学思想方法,是一种数学解题策略,对于何时需要分类讨论,则要视具体问题而定,并无死的规定。但可以在解题时不断地总结经验。
如果对于某个研究对象,若不对其分类就不能说清楚,则应分类讨论,另外,数学中的一些结论,公式、方法对于一般情形是正确的,但对某些特殊情形或说较为隐蔽的“个别”情况未必成立。这也是造成分类讨论的原因,因此在解题时,应注意挖掘这些个别情形进行分类讨论。常见的“个别”情形略举以下几例:
(1)“方程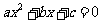 有实数解”转化为
有实数解”转化为 时忽略了了个别情形:当a=0时,方程有解不能转化为△≥0;
时忽略了了个别情形:当a=0时,方程有解不能转化为△≥0;
(2)等比数列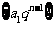 的前
的前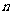 项和公式
项和公式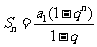 中有个别情形:
中有个别情形: 时,公式不再成立,而是Sn=na1。
时,公式不再成立,而是Sn=na1。
 设直线方程时,一般可设直线的斜率为k,但有个别情形:当直线与x轴垂直时,直线无斜率,应另行考虑。
设直线方程时,一般可设直线的斜率为k,但有个别情形:当直线与x轴垂直时,直线无斜率,应另行考虑。
(4)若直线在两轴上的截距相等,常常设直线方程为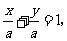 ,但有个别情形:a=0时,再不能如此设,应另行考虑。
,但有个别情形:a=0时,再不能如此设,应另行考虑。
例1.一条直线过点(5,2),且在x轴,y轴上截距相等,则这直线方程为( )
A. 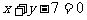 B.
B.
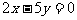

C. 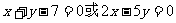 D.
D.
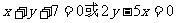

分析:设该直线在x轴,y轴上的截距均为a,
当a=0时,直线过原点,此时直线方程为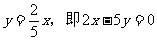 ;
;
当 时,设直线方程为
时,设直线方程为 ,方程为
,方程为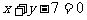 。
。
例2.

分析:

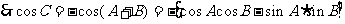

因此,只要根据已知条件,求出cosA,sinB即可得cosC的值。但是由sinA求cosA时,是一解还是两解?这一点需经过讨论才能确定,故解本题时要分类讨论。对角A进行分类。
解:

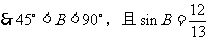





这与三角形的内角和为180°相矛盾。

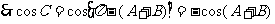

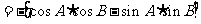
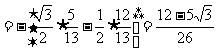

例3.已知圆x2+y2=4,求经过点P(2,4),且与圆相切的直线方程。
分析:容易想到设出直线的点斜式方程y-4=k(x-2)再利用直线与圆相切的充要条件:“圆心到切线的距离等于圆的半径”,待定斜率k,从而得到所求直线方程,但要注意到:过点P的直线中,有斜率不存在的情形,这种情形的直线是否也满足题意呢?因此本题对过点P的直线分两种情形:(1)斜率存在时,…(2)斜率不存在…
解(略):所求直线方程为3x-4y+10=0或x=2
例4.

分析:解对数不等式时,需要利用对数函数的单调性,把不等式转化为不含对数符号的不等式。而对数函数的单调性因底数a的取值不同而不同,故需对a进行分类讨论。
解: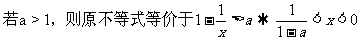



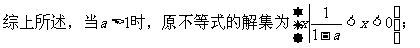



例5.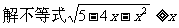

分析:解无理不等式,需要将两边平方后去根号,以化为有理不等式,而根据不等式的性质可知,只有在不等式两边同时为正时,才不改变不等号方向,因此应根据运算需求分类讨论,对x分类。
解: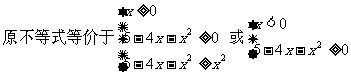

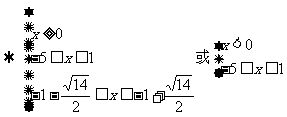

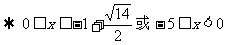
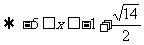



例6.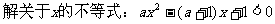

分析:这是一个含参数a的不等式,一定是二次不等式吗?不一定,故首先对二次项系数a分类:(1)a≠0(2)a=0,对于(2),不等式易解;对于(1),又需再次分类:a>0或a<0,因为这两种情形下,不等式解集形式是不同的;不等式的解是在两根之外,还是在两根之间。而确定这一点之后,又会遇到1与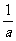 谁大谁小的问题,因而又需作一次分类讨论。故而解题时,需要作三级分类。
谁大谁小的问题,因而又需作一次分类讨论。故而解题时,需要作三级分类。
解: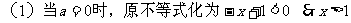

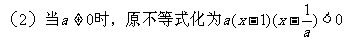

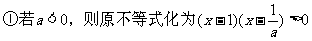

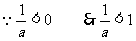


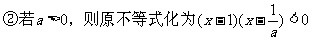

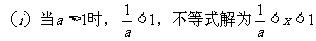

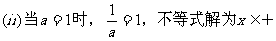



综上所述,得原不等式的解集为
 ;
;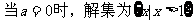 ;
;
 ;
;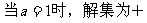 ;
;
 。
。
例7.已知等比数列的前n项之和为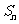 ,前n+1项之和为
,前n+1项之和为 ,公比q>0,令
,公比q>0,令 。
。
分析:对于等比数列的前n项和Sn的计算,需根据q是否为1分为两种情形:
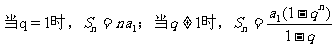



故还需对q再次分类讨论。
解: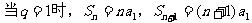
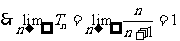

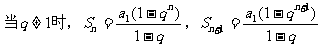


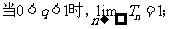

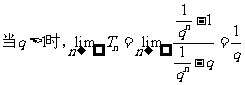

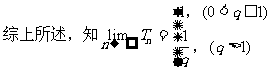

例8.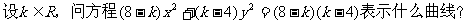

分析: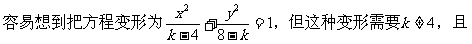

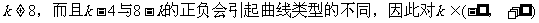
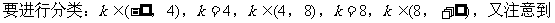

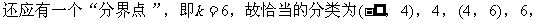
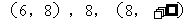

解:(1)当k=4时,方程变为4x2=0,即x=0,表示直线;
(2)当k=8时,方程变为4y2=0,即y=0,表示直线;


(i)当k<4时,方程表示双曲线;(ii)当4<k<6时,方程表示椭圆;
(iii)当k=6时,方程表示圆;(iv)当6<k<8时,方程表示椭圆;
(v)当k>8时,方程表示双曲线。
例9. 某车间有10名工人,其中4人仅会车工,3人仅会钳工,另外三人车工钳工都会,现需选出6人完成一件工作,需要车工,钳工各3人,问有多少种选派方案?
分析:如果先考虑钳工,因有6人会钳工,故有C63种选法,但此时不清楚选出的钳工中有几个是车钳工都会的,因此也不清楚余下的七人中有多少人会车工,因此在选车工时,就无法确定是从7人中选,还是从六人、五人或四人中选。同样,如果先考虑车工也会遇到同样的问题。因此需对全能工人进行分类:
(1)选出的6人中不含全能工人;(2)选出的6人中含有一名全能工人;(3)选出的6人中含2名全能工人;(4)选出的6人中含有3名全能工人。
解: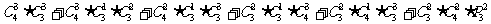



6.注意简化或避免分类讨论。
5.含参数问题的分类讨论是常见题型。
4.分类方法:明确讨论对象,确定对象的全体,确定分类标准,正确进行分类;逐类进行讨论,获取阶段性成果;归纳小结,综合出结论。
3.分类原则:分类对象确定,标准统一,不重复,不遗漏,分层次,不越级讨论。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com