
7.
以传送带的运动方向为x轴、以物块运动方向为y轴,建立平面直角坐标系。
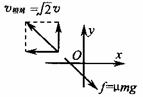 (1)先以传送带为参考系考虑问题:开始时物块相对于传送带的速度大小为
(1)先以传送带为参考系考虑问题:开始时物块相对于传送带的速度大小为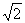 v,方向与x轴成1350。滑动摩擦力方向总与相对运动方向相反,即与x轴成-450。如图所示。由于物块受到的外力为恒力,它相地于传送带做的是匀减速直线运动,至速度减为0,就不再受摩擦力作用,将与传送带保持相对静止。
v,方向与x轴成1350。滑动摩擦力方向总与相对运动方向相反,即与x轴成-450。如图所示。由于物块受到的外力为恒力,它相地于传送带做的是匀减速直线运动,至速度减为0,就不再受摩擦力作用,将与传送带保持相对静止。
现在再转换到以地面为参考系:物块先做初速度为v(方向沿+y方向)、加速度为μg的匀变速曲线运动,加速度方向始终与皮带边缘成-45º夹角;然后物块随皮带一起沿+x方向做速度为v的匀速直线运动。
(2)以地面为参考系,对整个运动过程应用动能定理,得摩擦力对物块做的功W=0。
先以传送带为参考系求相对于传送带的位移。
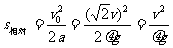 ,
,
根据功能关系,摩擦产生的热 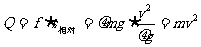 。
。
(3)物块在皮带上的运动(相对地面)x方向是初速为0的匀加速运动,vx=ax·t,y方向是初速为v的匀减速运动,vy=v-ay·t,其中ax=ay=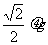 .合速度为
.合速度为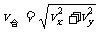 ,即
,即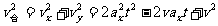 ,当
,当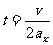 时,
时, 有最小值,最小速度
有最小值,最小速度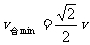 。
。
7.如图所示,水平传送带的皮带以恒定的速度v运动,一个质量为m小物块以一定的水平初速度v垂直皮带边缘滑上皮带,假设皮带足够大,物块与皮带间的动摩擦因数为μ。
(1)分析说明物块在皮带上做什么运动?
 (2)物块在皮带上运动的整个过程中,摩擦力对物块做的功及生的热。
(2)物块在皮带上运动的整个过程中,摩擦力对物块做的功及生的热。
(3)物块在皮带上运动的速度最小值。
6.(1)金属细圆柱产生的电动势为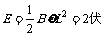
对整个系统由功能关系得
代入数据解得F=0.41N.
(2)S1闭合,S2拨到2位置,稳定后的金属细柱的角速度为ω′
由对整个系统由功能关系得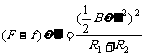
代入数据解得ω′=ω=10rad/s
S2拨到1稳定后电容器两端的电压为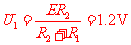 且上板带正电
且上板带正电
S2拨到2稳定后电容器两端的电压为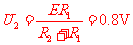 且上板带负电
且上板带负电
∴电容器上的电量变化为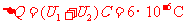
∴流过R3的电量为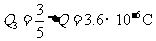
6.如图所示,水平放置的金属细圆环半径为0.1m,竖直放置的金属细圆柱(其半径比0.1m 小得多)的端面与金属圆环的上表面在同一平面内,圆柱的细轴通过圆环的中心O,将一质量和电阻均不计的导体棒一端固定一个质量为10g的金属小球,被圆环和细圆柱端面支撑,棒的一端有一小孔套在细轴O上,固定小球的一端可绕轴线沿圆环作圆周运动,小球与圆环的摩擦因数为0.1,圆环处于磁感应强度大小为4T、方向竖直向上的恒定磁场中,金属细圆柱与圆环之间连接如图电学元件,不计棒与轴及与细圆柱端面的摩擦,也不计细圆柱、圆环及感应电流产生的磁场,开始时S1断开,S2拨在1位置,R1=R3=4Ω,R2=R4=6Ω,C=30uF,求:
(1)S1闭合,问沿垂直于棒的方向以多大的水平外力作用于棒的A端,才能使棒稳定后以角速度10rad/s匀速转动?
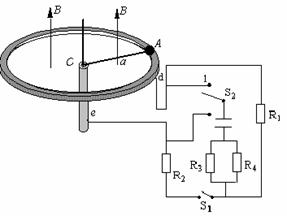 (2)S1闭合稳定后,S2由1拨到2位置,作用在棒上的外力不变,则至棒又稳定匀速转动的过程中,流经R3的电量是多少?
(2)S1闭合稳定后,S2由1拨到2位置,作用在棒上的外力不变,则至棒又稳定匀速转动的过程中,流经R3的电量是多少?
5.证明:导体中电流强度的微观表达式为:I=nes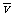
根据电阻定律:R =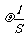
根据欧姆定律:R =
自由程内,电子在加速电场作用下,速度从0增加到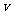 ,由动能定理:eU =
,由动能定理:eU =
又由于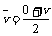 ,可得出电阻率
,可得出电阻率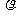 的表达式为:
的表达式为: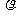 =
=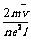
5.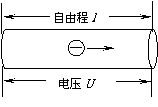 按照经典的电磁理论,电子在金属中运动的情形是这样的:在外加电场的作用下,自由电子发生定向运动,便产生了电流。电子在运动的过程中要不断地与金属离子发生碰撞,将动能交给金属离子,而自己的动能降为零,然后在电场的作用下重新开始加速运动(可看作匀加速运动),经加速运动一段距离后,再与金属离子发生碰撞。电子在两次碰撞之间走的平均距离叫自由程,用
按照经典的电磁理论,电子在金属中运动的情形是这样的:在外加电场的作用下,自由电子发生定向运动,便产生了电流。电子在运动的过程中要不断地与金属离子发生碰撞,将动能交给金属离子,而自己的动能降为零,然后在电场的作用下重新开始加速运动(可看作匀加速运动),经加速运动一段距离后,再与金属离子发生碰撞。电子在两次碰撞之间走的平均距离叫自由程,用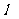 表示。电子运动的平均速度用
表示。电子运动的平均速度用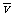 表示,导体单位体积内自由电子的数量为n,电子的质量为
表示,导体单位体积内自由电子的数量为n,电子的质量为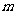 ,电子的电荷量为
,电子的电荷量为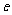 ,电流的表达式I=nes
,电流的表达式I=nes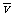 。请证明金属导体的电阻率
。请证明金属导体的电阻率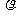 =
=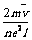 。
。
4.解:(1)由图: 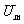 = 2.00×106V ,
= 2.00×106V , 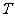 =1.00×10-7s
=1.00×10-7s
∴  V
V
(2)氘核在匀强磁场中做匀速圆周运动,有 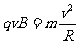
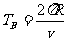 =
=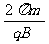
欲使氘核能持续做圆周运动,交流电的周期必须为: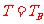
磁场的磁感强度: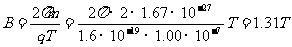
(3)氘核在D形盒运动一周时被加速两次,氘核获得E =5.00MeV能量而被加速的次数为 : 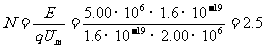
即氘核应被加速了3次
所需的运动时间为: 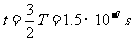
(4)、氘核的能量最大时,氘核运动的轨道半径最大:
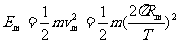
∴ 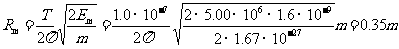
4.图甲所示为回旋加速器的原理示意图,一个扁圆柱形的金属盒子,盒子被分成两半(D
形电极),分别与高压交变电源的两极相连,在缝隙处形成一个交变电场,高压交流电源的
u-t图象如图乙所示,在两D形电极缝隙的中心靠近其中
一个D形盒处有一离子源K,D形电极位于匀强磁场中,磁场方向垂直于D形电极所在平面,
由下向上.从离子源K发出的氘核,在电场作用下,被加速进入盒中.又由于磁场的作用,
沿半圆形的轨道运动,并重新进入裂缝.这时电场方向已经改变,氘核在电场中又一次加速,
如此不断循环进行,最后在D形盒边缘被特殊装置引出.(忽略氘核在缝隙中运动的时间)
(1)写出图乙所示的高压交流电源的交流电压瞬时值的表达式;
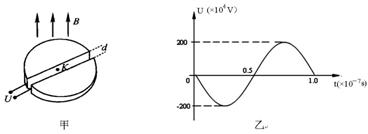 (2)将此电压加在回旋加速器上,给氘核加速,则匀强磁场的磁感强度应为多少?
(2)将此电压加在回旋加速器上,给氘核加速,则匀强磁场的磁感强度应为多少?
(3)若要使氘核获得5.00MeV的能量,需要多少时间?(设氘核正好在电压达到峰值时通过D形盒的狭缝)
(4)D形盒的最大半径R.
3.试题包括四个物理过程:
①弹簧解除锁定,AB相互弹开的过程,系统动量、机械能守恒。
②B滑上传送带匀减速运动的过程,用动能定理或动力学方法都可以求解。
③B随传送带匀加速返回的过程,此过程可能有两种情况:第一种情况是一直匀加速,第二种情况是先匀加速再匀速。
④B与A的碰撞过程。动量守恒且总动能不变。
(1)解除锁定弹开AB过程中,系统机械能守恒: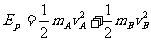 ①
①
由动量守恒有: mAvA=mBvB ②
由①②得: 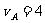 .0m/s
.0m/s 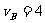 .0m/s
.0m/s
B滑上传送带后作匀减速运动,当速度减为零时,滑动的距离最远。
由动能定理得: 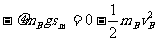 ③
③
所以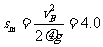 m
m
(2)物块B沿传送带向左返回时,先匀加速运动,物块速度与传送带速度相同才与传送带一起匀速运动,设物块B加速到传送带速度v需要滑动的距离为 ,
,
由 ④
④
得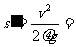 9.0m
9.0m 
说明物块B滑回水平面MN时的速度没有达到传送带速度。
 =4.0m/s
=4.0m/s
(3)设弹射装置给A做功为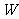 ,
, ⑤
⑤
AB碰后速度互换,B的速度 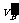 =
= ⑥
⑥
B要滑出平台Q端,由能量关系有: . ⑦
. ⑦
又mA=mB
所以,由⑤⑥⑦得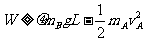 ⑧
⑧
解得 W ≥ 8.0 J
3.如图所示,光滑水平面MN上放两相同小物块A、B,左端挡板处有一弹射装置P,右端N处与水平传送带理想连接,传送带水平部分长度L=8.0 m,沿逆时针方向以恒定速度v=6.0 m/s匀速转动。物块A、B (大小不计)与传送带间的动摩擦因数
(大小不计)与传送带间的动摩擦因数 。物块A、B质量mA=mB=1.0kg。开始时A、B静止,A、B间压缩一轻质弹簧(二物块与弹簧不连接),贮有弹性势能Ep=16J。现解除锁定,弹簧弹开A、B。求:
。物块A、B质量mA=mB=1.0kg。开始时A、B静止,A、B间压缩一轻质弹簧(二物块与弹簧不连接),贮有弹性势能Ep=16J。现解除锁定,弹簧弹开A、B。求:
(1)物块B沿传送带向右滑动的最远距离。
(2)物块B滑回水平面MN的速度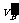 。
。
(3)若物体B返回水平面MN后与被弹射装置P弹回的A在水平面上相碰,且A、B碰后互换速度,则弹射装置P必须给A做多少功才能让AB碰后B能从Q端滑出。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com