3、青梅竹马：形容男女小时候天真无邪，在一起玩耍。多指男女间幼时的亲密感情。　　　

2、天花乱坠：指说得极为动听，多指夸大或不切实际。本词只能用来形容说。　　　

1、目无全牛：《庄子?养生主》中说，一个杀牛的人最初杀牛，眼睛看见的是全牛，三年以后，技术纯熟了，动刀时只看到皮骨间隙，而看不到全牛。用来形容技艺已达到十分纯熟的地步。本词易误用为贬义。　　　

2.有关“充要条件”、命题真伪的试题.主要是对数学概念有准确的记忆和深层次的理解.

试题以选择题、填空题为主，难度不大，要求对基本知识、基本题型，求解准确熟练.

1.有关集合的高考试题.考查重点是集合与集合之间的关系，近年试题加强了对集合的计算化简的考查，并向无限集发展，考查抽象思维能力，在解决这些问题时，要注意利用几何的直观性，注意运用文氏图解题方法的训练，注意利用特殊值法解题，加强集合表示方法的转换和化简的训练.

32.解：由|x－a|<2，得a－2<x<a+2，所以A={x|a－2<x<a+2}.

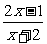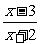由<1，得<0，即－2<x<3，所以B={x|－2<x<3}.

因为A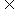B，所以，于是0≤a≤1.

评述：这是一道研究集合的包含关系与解不等式相结合的综合性题目.主要考查集合的概念及运算，解绝对值不等式、分式不等式和不等式组的基本方法.在解题过程中要注意利用不等式的解集在数轴上的表示方法.体现了数形结合的思想方法.

●命题趋与应试策略

31.解：由已知log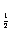(3－x)≥log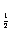4，因为y=log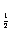x为减函数，所以3－x≤4.

由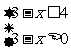，解得－1≤x<3.所以A={x|－1≤x<3}.

由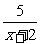≥1可化为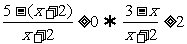

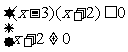解得－2<x≤3，所以B={x|－2<x≤3}.

于是_RA={x|x<－1或x≥3}.故_RA∩B={x|－2<x<1或x=3}

评述：本题主要考查集合、对数性质、不等式等知识，以及综合运用知识能力和运算能力.

30.解：由x²－6x+8>0，得(x－2)(x－4)>0，∴x<2或x>4.

由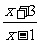>2，得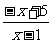>0，∴1<x<5.

∴原不等式组的解是x∈(1，2)∪(4，5)

评述：本题主要考查二次不等式、分式不等式的解法.

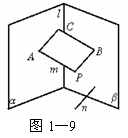
29.答案：m⊥α，n⊥β，α⊥βm⊥n，或m⊥n，m⊥α，

n⊥βα⊥β.(二者任选一个即可)

解析：假设①、③、④为条件，即m⊥n，n⊥β，m⊥α成立，

如图1-9，过m上一点P作PB∥n，则PB⊥m，PB⊥β，设垂足为B.

又设m⊥α的垂足为A，

过PA、PB的平面与α、β的交线l交于点C，

因为l⊥PA，l⊥PB，所以l⊥平面PAB，得l⊥AC，l⊥BC，∠ACB是二面角α－l－β的平面角.

显然∠APB+∠ACB=180°，因为PA⊥PB，所以∠ACB=90°，得α⊥β.由①、③、④推得②成立.

反过来，如果②、③、④成立，与上面证法类似可得①成立.

评述：本题主要考查线线、线面、面面之间关系的判定与性质，但题型较新颖，主要表现在：题目以立体几何知识为背景，给出了若干材料，要求学生能将其组装成具有一定逻辑关系的整体，解题的关键是将符号语言转化为图形语言.考查知识立足课本，对空间想象能力、分析问题的能力、操作能力和思维的灵活性等方面要求较高，体现了加强能力考查的方向.

28.答案：P∩_IQ

解析：阴影部分为_IQ(如图1-8)

显然，所求表达式为_IQ∩P=，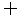

或_IQ∩(Q∩P)或_IQ∩(Q∪P)=.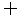

评述：本题考查集合的关系及运算.