4．(2009·上海高考)小球由地面竖直上抛，上升的最大高度为H，设所受阻力大小恒定，地面为零势能面．在上升至离地高度h处，小球的动能是势能的2倍，在下落至离地高度h处，小球的势能是动能的2倍，则h等于　　　　　　　　　　　 (　)

A.　 　　　　　B.　　　　　　　　 C. 　　　　　　　　D.

解析：设小球上升至离地面高度h时，速度为v₁，由地面上抛时速度为v₀，下落至离地面高度h处速度为v₂，空气阻力为F_f.

上升阶段：－mgH－F_fH＝－mv₀²

－mgh－F_fh＝mv₁²－mv₀²

2mgh＝mv₁²

下降阶段：mg(H－h)－F_f(H－h)＝mv₂²

mgh＝2×mv₂²

由以上各式联立得：h＝H.故选D.

答案：D

3．光滑斜面上有一个小球自高为h的A处由静止开始滚下，抵达光滑的水平面上的B点时的速度大小为v₀.光滑水平面上每隔相等的距离设置了一个与小球运动方向垂直的活动阻挡条，如图3所示，小球越过n条活动挡条后停下来．若让小球从h高处以初速度v₀滚下，则小球能越过的活动阻挡条的条数是(设小球每次越过活动阻挡条时损失的动能相等)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

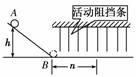
图3

A．n　　　　　　B．2n　　　　　 C．3n　 　　　　　　D．4n

解析：设每条阻挡条对小球做的功为W，当小球在水平面上滚动时，由动能定理有0－mv₀²＝nW，对第二次有0－mv₂²＝0－(mv₀²+mgh)＝NW，

又因为mv₀²＝mgh，联立以上三式解得N＝2n.

答案：B

2．在竖直平面内，有根光滑金属杆弯成如图2所示形状，相应的曲线方程为y＝Acosx，将一个光滑小环套在该金属杆上，并从x＝0、y＝A处以某一初速度沿杆向+x方向运动．运动过程中　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

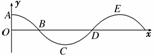
图2

A．小环在D点的加速度为零

B．小环在B点和D点的加速度相同

C．小环在C点的速度最大

D．小环在C点和E点的加速度方向相同

解析：小环在D点和B点的加速度是由环的重力沿杆切向分力产生的，由对称性可知，小环在两点的加速度的大小相同，方向不同，故A、B均错误；因C点最低，小环的重力势能最小，由机械能守恒知，小环在C点的速度最大，C正确；小环在C点和E点的加速度均为向心加速度，故方向相反，D错误．

答案：C

1．物体沿直线运动的v－t关系如图1所示，已知在第1秒内合外力对物体做的功为W，则　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(　)

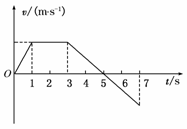
图1

A．从第1秒末到第3秒末合外力做功为4W

B．从第3秒末到第5秒末合外力做功为－2W

C．从第5秒末到第7秒末合外力做功为W

D．从第3秒末到第4秒末合外力做功为0.75W

解析：由题图知，第1秒末速度、第3秒末速度、第7秒速度大小关系：v₁＝v₃＝v₇，由题知W＝mv₁²－0，则由动能定理知第1秒末到第3秒末合外力做功W₂＝mv₃²－mv₁²＝0，故A错．第3秒末到第5秒末合外力做功W₃＝0－mv₃²＝－W，故B错．第5秒末到第7秒末合外力做功W₄＝mv₇²－0＝W，故C正确．第3秒末到第4秒末合外力做功W₅＝mv₄²－mv₃²；因v₄＝v₃，所以W₅＝－0.75 W．故D错误．

答案：C

16．(15分)随着现代科学技术的飞速发展，广寒宫中的嫦娥不再寂寞，古老的月球即将留下中华儿女的足迹．航天飞机将作为能往返于地球与太空、可以重复使用的太空飞行器，备受人们的喜爱．宇航员现欲乘航天飞机对在距月球表面高h处的圆轨道上运行的月球卫星进行维修．试根据你所学的知识回答下列问题：

(1)维修卫星时航天飞机的速度应为多大？

(2)已知地球自转周期为T₀，则该卫星每天可绕月球转几圈？(已知月球半径为R，月球表面的重力加速度为g_m，计算过程中可不计地球引力的影响，计算结果用h、R、g_m、T₀等表示)

解析：(1)根据万有引力定律，在月球上的物体

mg_m＝　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ①

卫星绕月球做圆周运动，设速度为v，则

G＝m　　　　　　　　　　　　　　　　　　　　　　　　　 ②

联立①②式解得：v＝

航天飞机与卫星在同一轨道上，速度与卫星速度相同．

(2)设卫星运动周期为T，

则G＝m()²(R+h)

解得：T＝2π ＝2π

则卫星每天绕月球运转的圈数为＝ .

答案：(1) 　(2)

15．(14分)我国射击运动员曾多次在国际大赛中为国争光，在2008年北京奥运会上又夺得射击冠军．我们以打靶游戏来了解射击运动．某人在塔顶进行打靶游戏，如图9所示，已知塔高H＝45 m，在与塔底部水平距离为x处有一电子抛靶装置，圆形靶可被竖直向上抛出，初速度为v₁，且大小可以调节．当该人看见靶被抛出时立即射击，子弹以v₂＝100 m/s的速度水平飞出．不计人的反应时间及子弹在枪膛中的运动时间，且忽略空气阻力及靶的大小(取g＝10 m/s²)．

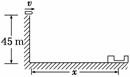
图9

(1)当x的取值在什么范围时，无论v₁多大靶都不能被击中？

(2)若x＝200 m，v₁＝15 m/s时，试通过计算说明靶能否被击中？

解析：(1)欲使靶不被击中，抛靶装置应在子弹射程范围外．由H＝gt²，x＝v₂t代入数据得x＝300 m；故x的取值范围应为x＞300 m.

(2)设经过时间t₁，子弹恰好在抛靶装置正上方，此时靶离地面h₁，子弹下降了h₂，h₁＝v₁t₁－gt₁²，h₂＝gt₁²，x＝v₂t₁，联立以上各式解得h₁＝10 m，h₂＝20 m．所以h₁+h₂≠H，靶不能被击中．

答案：(1)x＞300 m　(2)见解析

14．(14分)如图8所示，水平转盘上放有质量为m的物块，当物块到转轴的距离为r时，连接物块和转轴的绳刚好被拉直(绳上张力为零)，物块和转盘间最大静摩擦力是其正压力的μ倍．求：

(1)当转盘的角速度ω₁＝ 时，细绳的拉力F₁；　　　　　　　　　　　　 图8

(2)当转盘的角速度ω₂＝ 时，细绳的拉力F₂.

解析：设角速度为ω₀时，绳恰好拉直而无张力，有

μmg＝mω₀²·r得ω₀＝

(1)由于ω₁＝＜ω₀，故绳未拉紧，此时静摩擦力未达到最大值，F₁＝0.

(2)由于ω₂＝＞ω₀，故绳被拉紧，

由F₂+μmg＝mω₂²·r

得F₂＝μmg.

答案：(1)0　(2)μmg

13．(12分)A、B两小球同时从距地面高为h＝15 m处的同一点抛出，初速度大小均为v₀＝10 m/s.A竖直向下抛出，B球水平抛出，空气阻力不计，重力加速度取g＝10 m/s².求：

(1)A球经过多长时间落地？

(2)A球落地时，A、B两球间的距离是多少？

解析：(1)A球做竖直下抛运动　h＝v₀t+gt²

将h＝15 m、v₀＝10 m/s代入，可得t＝1 s.

(2)B球做平抛运动，x＝v₀t，y＝gt²

将v₀＝10 m/s、t＝1 s代入，可得x＝10 m，y＝5 m.

此时A球与B球的距离为L＝

将x、y、h数据代入，得L＝10 m.

答案：(1)1 s　(2)10 m

12．“嫦娥一号”于2009年3月1日下午4时13分成功撞月，从发射到撞落历时433天，标志着我国一期探月工程圆满结束．其中，卫星发射过程先在近地圆轨道绕行3周，再长途跋涉进入近月圆轨道绕月飞行．若月球表面的重力加速度为地球表面重力加速度的1/6，月球半径为地球半径的1/4，据以上信息得　　　　　　　　　　 　　　　　(　)

A．绕月与绕地飞行周期之比为∶

B．绕月与绕地飞行周期之比为∶

C．绕月与绕地飞行向心加速度之比为1∶6

D．月球与地球质量之比为1∶96

解析：本题考查万有引力和重力的关系以及天体的运动问题．卫星在绕月和绕地飞行时，都是星体表面的重力提供了卫星运动的向心力，即＝mg＝ma＝mr，故可得T∝ ，A、C正确；M∝gr²，可得D正确．

答案：ACD

11．(2010·连云港模拟)飞机在水平地面上空的某一高度水平匀速飞行，每隔相等时间投放一个物体．如果以第一个物体a的落地点为坐标原点、飞机飞行方向为横坐标的正方向，在竖直平面内建立直角坐标系．如图7所示是第5个物体e离开飞机时，抛出的5个物体(a、b、c、d、e)在空间位置的示意图，其中可能的是　　　　　　　　　　 (　)

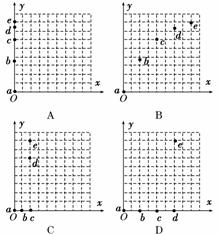
图7

解析：本题考查平抛运动的特点．物体被抛出时的水平速度相同，如果第一个物体a都没有落地，那么所有物体在竖直方向应该排成一排，所以A对；如果先投出的物体已经落地，相邻物体的水平距离应该相等，没有落地的在竖直方向仍排成一排，所以B选项错误，C、D皆正确．

答案：ACD