6．(2009·北京文，6)“α＝”是“cos 2α＝”的　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．充分而不必要条件　 　　　　　　　　　　　 B．必要而不充分条件

C．充分必要条件　 　　　　　　　　　　　　　　 D．既不充分也不必要条件

解析　当α＝时，cos　 2α＝cos＝；而当α＝－时，cos 2α＝cos＝，这说明当cos 2α＝时，α除外还可以取其他的值．所以“α＝”是“cos 2α＝”的充分而不必要条件．

答案　A

5．(2010·枣庄一模)集合A＝{x||x|≤4，x∈R}，B＝{x|x<a}，则“A⊆B”是“a>5”的(　)

A．充分不必要条件　 　　　　　　　　　　　　　 B．必要不充分条件

C．充要条件　 　　　　　　　　　　　　　　　　　　 D．既不充分也不必要条件

解析　A＝{x|－4≤x≤4}，若A⊆B，则a>4，

a>4D⇒/a>5，但a>5⇒a>4.

故“A⊆B”是“a>5”的必要不充分条件．

答案　B

4．(2010·衡阳四校联考)已知A＝{x||x－1|≥1，x∈R}，B＝{x|log₂x>1，x∈R}，则“x∈A”是“x∈B”的　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．充分不必要条件　 　　　　　　　　　　　　　 B．必要不充分条件

C．充分必要条件　 　　　　　　　　　　　　　　 D．既不充分也不必要条件

解析　A＝{x|x≥2或x≤0}，B＝{x|x>2}，

x∈AD⇒/x∈B，但x∈B⇒x∈A.

答案　B

3．(2008·广东文，8)命题“若函数f(x)＝log_ax(a>0，a≠1)在其定义域内是减函数，则log_a2<0”

的逆否命题是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．若log_a2≥0，则函数f(x)＝log_ax(a>0，a≠1)在其定义域内不是减函数

B．若log_a2<0，则函数f(x)＝log_ax(a>0，a≠1)在其定义域内不是减函数

C．若log_a2≥0，则函数f(x)＝log_ax(a>0，a≠1)在其定义域内是减函数

D．若log_a2<0，则函数f(x)＝log_ax(a>0，a≠1)在其定义域内是减函数

解析　由互为逆否命题的关系可知，原命题的逆否命题为：若log_a2≥0，则函数f(x)＝

log_ax(a>0，a≠1)在其定义域内不是减函数．

答案　A

2．(2009·浙江理，2)已知a，b是实数，则“a>0且b>0”是“a+b>0且ab>0”的(　)

A．充分而不必要条件　 　　　　　　　　　　　 B．必要而不充分条件

C．充分必要条件　 　　　　　　　　　　　　　　 D．既不充分也不必要条件

解析　当a>0且b>0时，一定有a+b>0且ab>0.反之，当a+b>0且ab>0时，一定有a>0，

b>0.故“a>0且b>0”是“a+b>0且ab>0”的充要条件．

答案　C

1．(2009·重庆文，2)命题“若一个数是负数，则它的平方是正数”的逆命题是(　)

A．“若一个数是负数，则它的平方不是正数”

B．“若一个数的平方是正数，则它是负数”

C．“若一个数不是负数，则它的平方不是正数”

D．“若一个数的平方不是正数，则它不是负数”

解析　原命题的逆命题：若一个数的平方是正数，则它是负数．

答案　B

12．(14分)(2010·揭阳模拟)已知二次函数f(x)＝ax²+x有最小值，不等式f(x)<0的解集为A.

(1)求集合A；

(2)设集合B＝{x||x+4|<a}，若集合B是集合A的子集，求a的取值范围．

解　(1)∵二次函数f(x)＝ax²+x有最小值，∴a>0.

∴解不等式f(x)＝ax²+x<0，得集合A＝.

(2)由B＝{x||x+4|<a}，解得B＝(－a－4，a－4)，

∵集合B是集合A的子集，

∴解得0<a≤－2.

§1.2　命题及其关系、充分条件与必要条件

11．(13分)(2009·南阳调研)已知集合A＝{x|x²－2x－3≤0}，B＝{x|x²－2mx+m²－4≤0，x∈R，

m∈R}．

(1)若A∩B＝[0,3]，求实数m的值；

(2)若A⊆∁_RB，求实数m的取值范围．

解　由已知得A＝{x|－1≤x≤3}，

B＝{x|m－2≤x≤m+2}．

(1)∵A∩B＝[0,3]，∴　∴m＝2.

(2)∁_RB＝{x|x<m－2或x>m+2}，∵A⊆∁_RB，

∴m－2>3或m+2<－1，即m>5或m<－3.

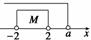
10．(13分)(2010·新乡阶段检测)已知全集为R，集合M＝{x||x|<2，x∈R}，P＝{x|x≥a}，并

且M?∁_RP，求a的取值范围．

解　M＝{x||x|<2}＝{x|－2<x<2}，∁_RP＝{x|x<a}．

∵M?∁_RP，∴由数轴知a≥2.

9．(2009·北京文，14)设A是整数集的一个非空子集，对于k∈A，如果k－1∉A，且k+1∉A，

那么称k是A的一个“孤立元”．给定S＝{1,2,3,4,5,6,7,8}，由S的3个元素构成的所有

集合中，不含“孤立元”的集合共有______个．

解析　由题意知，不含“孤立元”的集合有：{1,2,3}，{2,3,4}，{3,4,5}，{4,5,6}，{5,6,7}，

{6,7,8}，共有6个集合．

答案　6三、解答题(共40分)