
1.[答案]i
[解析]设z=a+bi,则(a+bi )(1+i)
=1-i,即a-b+(a+b)i=1-i,由 ,解得a=0,b=-1,所以z=-i,
,解得a=0,b=-1,所以z=-i, =i
=i
1. 若复数 z 满足z (1+i) =1-i (I是虚数单位),则其共轭复数 =__________________ .
=__________________ .
23.[解](1)由 得
得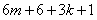 ,
,
整理后,可得
 、
、 ,
, 为整数
为整数
 不存在
不存在 、
、 ,使等式成立。
,使等式成立。
(2)当 时,则
时,则
 即
即 ,其中
,其中 是大于等于
是大于等于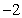 的整数
的整数
反之当 时,其中
时,其中 是大于等于
是大于等于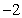 的整数,则
的整数,则 ,
,
显然 ,其中
,其中

 、
、 满足的充要条件是
满足的充要条件是 ,其中
,其中 是大于等于
是大于等于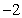 的整数
的整数
(3)设
当 为偶数时,
为偶数时,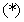 式左边为偶数,右边为奇数,
式左边为偶数,右边为奇数, 

当 为偶数时,
为偶数时,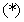 式不成立。
式不成立。
由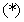 式得
式得 ,整理得
,整理得
当 时,符合题意。
时,符合题意。
当 ,
, 为奇数时,
为奇数时,


 由
由 ,得
,得

 当
当 为奇数时,此时,一定有
为奇数时,此时,一定有 和
和 使上式一定成立。
使上式一定成立。
 当
当 为奇数时,命题都成立。
为奇数时,命题都成立。 

23.(本题满分18分)本题共有3个小题,第1小题满分5分,第2小题满分5分,第3小题满分8分.
已知 是公差为d的等差数列,
是公差为d的等差数列, 是公比为q的等比数列
是公比为q的等比数列
(1)若  ,是否存在
,是否存在 ,有
,有 ?请说明理由;
?请说明理由;
(2)若 (a、q为常数,且aq
(a、q为常数,且aq 0)对任意m存在k,有
0)对任意m存在k,有 ,试求a、q满足的充要条件;
,试求a、q满足的充要条件;
(3)若 试确定所有的p,使数列
试确定所有的p,使数列 中存在某个连续p项的和式数列中
中存在某个连续p项的和式数列中 的一项,请证明.
的一项,请证明. 

22.[解](1)设双曲线 的方程为
的方程为
 ,解额
,解额 双曲线
双曲线 的方程为
的方程为
(2)直线 ,直线
,直线
由题意,得 ,解得
,解得
(3)[证法一]设过原点且平行于 的直线
的直线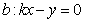
则直线 与
与 的距离
的距离 当
当 时,
时,
又双曲线 的渐近线为
的渐近线为



 双曲线
双曲线 的右支在直线
的右支在直线 的右下方,
的右下方,
 双曲线
双曲线 右支上的任意点到直线
右支上的任意点到直线 的距离大于
的距离大于 。
。
故在双曲线 的右支上不存在点
的右支上不存在点 ,使之到直线
,使之到直线 的距离为
的距离为
[证法二]假设双曲线 右支上存在点
右支上存在点 到直线
到直线 的距离为
的距离为 ,
,
则
由(1)得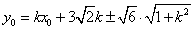
设 ,
,
当 时,
时, ;
;

将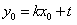 代入(2)得
代入(2)得
 ,
, 


 方程
方程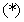 不存在正根,即假设不成立,
不存在正根,即假设不成立,
故在双曲线 的右支上不存在点
的右支上不存在点 ,使之到直线
,使之到直线 的距离为
的距离为
22.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分4分,第3小题满分8分.
已知双曲线C的中心是原点,右焦点为F ,一条渐近线m:
,一条渐近线m: ,设过点A
,设过点A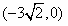 的直线l的方向向量
的直线l的方向向量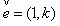 。
。
(1) 求双曲线C的方程;
(2) 若过原点的直线 ,且a与l的距离为
,且a与l的距离为 ,求K的值;
,求K的值;
(3) 证明:当 时,在双曲线C的右支上不存在点Q,使之到直线l的距离为
时,在双曲线C的右支上不存在点Q,使之到直线l的距离为 .
.
21.(本题满分16分)本题共有2个小题,第1小题满分6分,第2小题满分10分 .有时可用函数

描述学习某学科知识的掌握程度.其中 表示某学科知识的学习次数(
表示某学科知识的学习次数( ),
),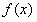 表示对该学科知识的掌握程度,正实数a与学科知识有关.
表示对该学科知识的掌握程度,正实数a与学科知识有关.
(1)证明:当x  7时,掌握程度的增长量f(x+1)- f(x)总是下降;
7时,掌握程度的增长量f(x+1)- f(x)总是下降;
(2)根据经验,学科甲、乙、丙对应的a的取值区间分别为(115,121],(121,127],
(127,133].当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.
21题。证明(1)当 时,
时,
而当 时,函数
时,函数 单调递增,且
单调递增,且
故函数 单调递减
单调递减 

当 时,掌握程度的增长量
时,掌握程度的增长量 总是下降
总是下降
(2)有题意可知
整理得
解得 …….13分
…….13分
由此可知,该学科是乙学科……………..14分
20.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分 .
已知ΔABC的角A、B、C所对的边分别是a、b、c,设向量 ,
,
 ,
,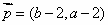 .
.
(1) 若 //
// ,求证:ΔABC为等腰三角形;
,求证:ΔABC为等腰三角形;
(2) 若 ⊥
⊥ ,边长c = 2,角C =
,边长c = 2,角C =  ,求ΔABC的面积 .
,求ΔABC的面积 .
20题。证明:(1)
即 ,其中R是三角形ABC外接圆半径,
,其中R是三角形ABC外接圆半径,
 为等腰三角形
为等腰三角形
解(2)由题意可知

由余弦定理可知,
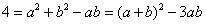





19.解:原方程的根为 




19.(本题满分14分)
已知复数 (a、b
(a、b )(I是虚数单位)是方程
)(I是虚数单位)是方程 的根 . 复数
的根 . 复数 (
( )满足
)满足 ,求 u 的取值范围 .
,求 u 的取值范围 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com