11.(2009全国卷Ⅱ文)已知圆O：和点A(1，2)，则过A且与圆O相切的直线与两坐标轴围成的三角形的面积等于　 　　　　　

　 答案： 　

解析：由题意可直接求出切线方程为y-2=(x-1)，即x+2y-5=0,从而求出在两坐标轴上的截距分别是5和，所以所求面积为。

10.(2009江苏卷)如图，在平面直角坐标系中，为椭圆的四个顶点，为其右焦点，直线与直线相交于点T，线段与椭圆的交点恰为线段的中点，则该椭圆的离心率为　　 　　　　.

[解析] 考查椭圆的基本性质，如顶点、焦点坐标，离心率的计算等。以及直线的方程。

直线的方程为：；

直线的方程为：。二者联立解得：， 　　

则在椭圆上，

， 　　

解得：

9.(2009北京理)椭圆的焦点为，点在

椭圆上，若，则_________；

的小大为__________.　　　　　　　　　　　　　　

[答案]　　　　　　　　　　　　　　　　　

[解析]本题主要考查椭圆的定义、焦点、长轴、短轴、焦距之间的关系以及余弦定理. 属

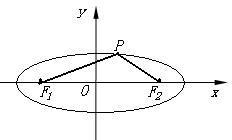于基础知识、基本运算的考查.

　　　　 ∵，

∴，

∴，

又，　　　　　 (第12题解答图)

∴，

又由余弦定理，得，

∴，故应填.

8.(2009北京理)设是偶函数，若曲线在点处的切线的斜率为1，则该曲线在处的切线的斜率为_________.

[答案]

[解析]本题主要考查导数与曲线在某一点处切线的斜率的概念. 属于基础知识、基本运算

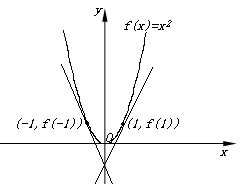的考查.

取，如图，采用数形结合法，

易得该曲线在处的切线的斜率为.

故应填.

(第11题解答图)

7.(2009北京文)椭圆的焦点为，点P在椭圆上，若，则　　　　 ；的大小为　　　　 .

[答案]

.w[解析]本题主要考查椭圆的定义、焦点、长轴、短轴、焦距之间的关系以及余弦定理. 属于基础知识、基本运算的考查.

　　　　 ∵，

∴，

∴，

又，∴，　 (第13题解答图)

又由余弦定理，得，

∴，故应填.

6.(2009重庆卷理)已知双曲线的左、右焦点分别为，若双曲线上存在一点使，则该双曲线的离心率的取值范围是　　　　　 ．

解法1，因为在中，由正弦定理得

则由已知，得，即，且知点P在双曲线的右支上，

设点由焦点半径公式，得则

解得由双曲线的几何性质知，整理得

解得，故椭圆的离心率

解法2 由解析1知由双曲线的定义知 　　

，由椭圆的几何性质知所以以下同解析1.

5.(2009重庆卷文)已知椭圆的左、右焦点分别为，若椭圆上存在一点使，则该椭圆的离心率的取值范围为　　　　　 ．

[答案]

.　　 解法1，因为在中，由正弦定理得

则由已知，得，即

设点由焦点半径公式，得则

记得由椭圆的几何性质知，整理得

解得，故椭圆的离心率

解法2 由解析1知由椭圆的定义知 　　

，由椭圆的几何性质知所以以下同解析1.

4.(2009湖北卷文)过原点O作圆x²+y^2‑－6x－8y+20=0的两条切线，设切点分别为P、Q，则线段PQ的长为　　　　　　 。

[答案]4

[解析]可得圆方程是又由圆的切线性质及在三角形中运用正弦定理得

3.(2009天津卷理)若圆与圆(a>0)的公共弦的长为，

则___________ 　　　。

[考点定位]本小题考查圆与圆的位置关系，基础题。

解析：由知的半径为，由图可知解之得

2.(2009全国卷Ⅰ文)若直线被两平行线所截得的线段的长为，则的倾斜角可以是

　　　　 ①　 ②　 ③　 ④　　 ⑤ 　　

其中正确答案的序号是　　　　　 　.(写出所有正确答案的序号)

[解析]本小题考查直线的斜率、直线的倾斜角、两条平行线间的距离，考查数形结合的思想。

解：两平行线间的距离为，由图知直线与的夹角为，的倾斜角为，所以直线的倾斜角等于或。故填写①或⑤