
27.(2009陕西卷理)(本小题满分12分)
已知双曲线C的方程为 ,离心率
,离心率 ,顶点到渐近线的距离为
,顶点到渐近线的距离为 。
。
(I)求双曲线C的方程;
(II)如图,P是双曲线C上一点,A,B两点在双曲线C的两条渐近线上,且分别位于第一、二象限,若 ,求
,求 面积的取值范围。
面积的取值范围。
26.(2009陕西卷文)(本小题满分12分)
已知双曲线C的方程为 ,离心率
,离心率 ,顶点到渐近线的距离为
,顶点到渐近线的距离为 。21世纪教育网
。21世纪教育网 

(I) 求双曲线C的方程;
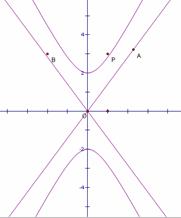 (II)如图,P是双曲线C上一点,A,B两点在双曲线C的两条渐近线上,且分别位于第一、二象限,若
(II)如图,P是双曲线C上一点,A,B两点在双曲线C的两条渐近线上,且分别位于第一、二象限,若 ,求
,求 面积的取值范围。
面积的取值范围。
解析:
解法1(Ⅰ)由题意知,双曲线C的顶点(0,a)到渐近线 ,
,
所以 所以
所以
由
所以曲线 的方程是
的方程是
(Ⅱ)由(Ⅰ)知双曲线C的两条渐近线方程为
设
由
将P点的坐标代入
因为

又
所以
记
则
由
又S(1)=2,
当 时,
时, 面积取到最小值
面积取到最小值 ,当当
,当当 时,
时, 面积取到最大值
面积取到最大值
所以 面积范围是
面积范围是
解答2(Ⅰ)由题意知,双曲线C的顶点(0,a)到渐近线 ,
,

由
所以曲线 的方程是
的方程是 .
.
(Ⅱ)设直线AB的方程为
由题意知
由
由

将P点的坐标代入 得
得
设Q为直线AB与y轴的交点,则Q点的坐标为(0,m)
 =
=

以下同解答1
25.(2009宁夏海南卷理)(本小题满分12分)
已知椭圆C的中心为直角坐标系xOy的原点,焦点在s轴上,它的一个顶点到两个焦点的距离分别是7和1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若P为椭圆C上的动点,M为过P且垂直于x轴的直线上的点, =λ,求点M的轨迹方程,并说明轨迹是什么曲线。
=λ,求点M的轨迹方程,并说明轨迹是什么曲线。
解:(Ⅰ)设椭圆长半轴长及半焦距分别为 ,由已知得
,由已知得
 ,
,
所以椭圆 的标准方程为
的标准方程为


(Ⅱ)设 ,其中
,其中 。由已知
。由已知 及点
及点 在椭圆
在椭圆 上可得
上可得
 。
。
整理得 ,其中
,其中 。
。
(i) 时。化简得
时。化简得
所以点 的轨迹方程为
的轨迹方程为 ,轨迹是两条平行于
,轨迹是两条平行于 轴的线段。
轴的线段。
(ii) 时,方程变形为
时,方程变形为 ,其中
,其中
当 时,点
时,点 的轨迹为中心在原点、实轴在
的轨迹为中心在原点、实轴在 轴上的双曲线满足
轴上的双曲线满足 的部分。
的部分。
当 时,点
时,点 的轨迹为中心在原点、长轴在
的轨迹为中心在原点、长轴在 轴上的椭圆满足
轴上的椭圆满足 的部分;
的部分;
当 时,点
时,点 的轨迹为中心在原点、长轴在
的轨迹为中心在原点、长轴在 轴上的椭圆;
轴上的椭圆;
24.(2009辽宁卷理)(本小题满分12分)
已知,椭圆C过点A ,两个焦点为(-1,0),(1,0)。
,两个焦点为(-1,0),(1,0)。
(3) 求椭圆C的方程; 

(4) E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值。
(20)解:
(Ⅰ)由题意,c=1,可设椭圆方程为 ,解得
,解得 ,
, (舍去)
(舍去)
所以椭圆方程为 。
……………4分
。
……………4分
(Ⅱ)设直线AE方程为: ,代入
,代入 得
得

设 ,
, ,因为点
,因为点 在椭圆上,所以
在椭圆上,所以

 ………8分
………8分
又直线AF的斜率与AE的斜率互为相反数,在上式中以-K代K,可得


所以直线EF的斜率
即直线EF的斜率为定值,其值为 。
……12分
。
……12分
23.(2009辽宁卷文)(本小题满分12分)
已知,椭圆C以过点A(1, ),两个焦点为(-1,0)(1,0)。
),两个焦点为(-1,0)(1,0)。
(1) 求椭圆C的方程;
(2) E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值。 

(22)解:(Ⅰ)由题意,c=1,可设椭圆方程为 。
。 

因为A在椭圆上,所以 ,解得
,解得 =3,
=3, =
= (舍去)。
(舍去)。
所以椭圆方程为  . ......4分
. ......4分
(Ⅱ)设直线AE方程:得 ,代入
,代入 得
得 


设E( ,
, ),F(
),F( ,
, ).因为点A(1,
).因为点A(1, )在椭圆上,所以
)在椭圆上,所以
 ,
, 

 。 .......8分
。 .......8分
又直线AF的斜率与AE的斜率互为相反数,在上式中以 代
代 ,可得
,可得
 ,
, 

 。
。
所以直线EF的斜率 。
。
即直线EF的斜率为定值,其值为 。
.......12分
。
.......12分
19.[解析]
解法一:
(Ⅰ)当曲线C为半圆时, 如图,由点T为圆弧
如图,由点T为圆弧 的三等分点得∠BOT=60°或120°.
的三等分点得∠BOT=60°或120°.
(1)当∠BOT=60°时, ∠SAE=30°.
又AB=2,故在△SAE中,有
(2)当∠BOT=120°时,同理可求得点S的坐标为 ,综上,
,综上,

(Ⅱ)假设存在 ,使得O,M,S三点共线.
,使得O,M,S三点共线.
由于点M在以SB为直线的圆上,故 .
.
显然,直线AS的斜率k存在且k>0,可设直线AS的方程为 .
.
由
设点
故 ,从而
,从而 .
.
亦即

由 得
得
由 ,可得
,可得 即
即

经检验,当 时,O,M,S三点共线. 故存在
时,O,M,S三点共线. 故存在 ,使得O,M,S三点共线.
,使得O,M,S三点共线.
解法二:
(Ⅰ)同解法一.
(Ⅱ)假设存在a,使得O,M,S三点共线.
由于点M在以SO为直径的圆上,故 .
.
显然,直线AS的斜率k存在且K>0,可设直线AS的方程为
由
设点 ,则有
,则有
故

由 所直线SM的方程为
所直线SM的方程为
O,S,M三点共线当且仅当O在直线SM上,即 .
.

故存在 ,使得O,M,S三点共线.
,使得O,M,S三点共线.
22.(2009福建卷理)(本小题满分13分)
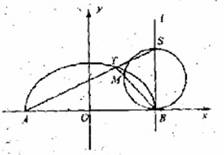 已知A,B 分别为曲线C:
已知A,B 分别为曲线C:  +
+ =1(y
=1(y 0,a>0)与x轴
0,a>0)与x轴
的左、右两个交点,直线 过点B,且与
过点B,且与 轴垂直,S为
轴垂直,S为 上
上
异于点B的一点,连结AS交曲线C于点T.
(1)若曲线C为半圆,点T为圆弧 的三等分点,试求出点S的坐标;
的三等分点,试求出点S的坐标;
(II)如图,点M是以SB为直径的圆与线段TB的交点,试问:是否存在 ,使得O,M,S三点共线?若存在,求出a的值,若不存在,请说明理由。
,使得O,M,S三点共线?若存在,求出a的值,若不存在,请说明理由。 

21.(2009湖南卷文)(本小题满分13分)
已知椭圆C的中心在原点,焦点在 轴上,以两个焦点和短轴的两个端点
轴上,以两个焦点和短轴的两个端点
为顶点的四边形是一个面积为8的正方形(记为Q).
(Ⅰ)求椭圆C的方程;
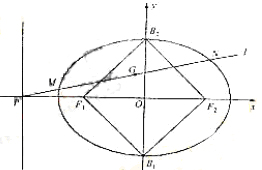
(Ⅱ)设点P是椭圆C的左准线与 轴的交点,过点P的直线
轴的交点,过点P的直线 与椭圆C相交于M,N两点,当线段MN的中点落在正方形Q内(包括边界)时,求直线
与椭圆C相交于M,N两点,当线段MN的中点落在正方形Q内(包括边界)时,求直线 的斜率的取值范围。
的斜率的取值范围。
解: (Ⅰ)依题意,设椭圆C的方程为 焦距为
焦距为 ,
,
由题设条件知, 所以
所以
故椭圆C的方程为 .
.
(Ⅱ)椭圆C的左准线方程为 所以点P的坐标
所以点P的坐标 ,
,
显然直线 的斜率
的斜率 存在,所以直线
存在,所以直线 的方程为
的方程为 。
。 

如图,设点M,N的坐标分别为 线段MN的中点为G
线段MN的中点为G ,
,
由 得
得 .
……①
.
……①
由 解得
解得 . ……②
. ……②
因为 是方程①的两根,所以
是方程①的两根,所以 ,于是
,于是
 =
= ,
, .
.
因为 ,所以点G不可能在
,所以点G不可能在 轴的右边,
轴的右边,
又直线 ,
, 方程分别为
方程分别为
所以点 在正方形
在正方形 内(包括边界)的充要条件为
内(包括边界)的充要条件为
 即
即 亦即
亦即


解得 ,此时②也成立. 21世纪教育网
,此时②也成立. 21世纪教育网 

故直线 斜率的取值范围是
斜率的取值范围是
20.(2009全国卷Ⅱ理)(本小题满分12分)
已知椭圆 的离心率为
的离心率为 ,过右焦点F的直线
,过右焦点F的直线 与
与 相交于
相交于 、
、 两点,当
两点,当 的斜率为1时,坐标原点
的斜率为1时,坐标原点 到
到 的距离为
的距离为
(I)求 ,
, 的值;
的值;
(II) 上是否存在点P,使得当
上是否存在点P,使得当 绕F转到某一位置时,有
绕F转到某一位置时,有 成立?
成立?
若存在,求出所有的P的坐标与 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。
解:(I)设 ,直线
,直线 ,由坐标原点
,由坐标原点 到
到 的距离为
的距离为
则 ,解得
,解得  .又
.又 .
.
(II)由(I)知椭圆的方程为 .设
.设 、
、

由题意知 的斜率为一定不为0,故不妨设
的斜率为一定不为0,故不妨设 
代入椭圆的方程中整理得 ,显然
,显然 。
。
由韦达定理有:
 ........①
........①
.假设存在点P,使 成立,则其充要条件为:
成立,则其充要条件为:
点 ,点P在椭圆上,即
,点P在椭圆上,即 。
。
整理得 。
。 

又 在椭圆上,即
在椭圆上,即 .
.
故 ................................②
................................②
将 及①代入②解得
及①代入②解得
 ,
, =
= ,即
,即 .
.
当 ;
;
当 .
.
评析:处理解析几何题,学生主要是在“算”上的功夫不够。所谓“算”,主要讲的是算理和算法。算法是解决问题采用的计算的方法,而算理是采用这种算法的依据和原因,一个是表,一个是里,一个是现象,一个是本质。有时候算理和算法并不是截然区分的。例如:三角形的面积是用底乘高的一半还是用两边与夹角的正弦的一半,还是分割成几部分来算?在具体处理的时候,要根据具体问题及题意边做边调整,寻找合适的突破口和切入点。
19.(2009四川卷文)(本小题满分12分) 

已知椭圆 的左、右焦点分别为
的左、右焦点分别为 ,离心率
,离心率 ,右准线方程为
,右准线方程为 。
。
(I)求椭圆的标准方程;
(II)过点 的直线
的直线 与该椭圆交于
与该椭圆交于 两点,且
两点,且 ,求直线
,求直线 的方程。
的方程。
[解析](I)由已知得 ,解得
,解得


∴ 
∴ 所求椭圆的方程为 …………………………………4分
…………………………………4分
(II)由(I)得 、
、
①若直线 的斜率不存在,则直线
的斜率不存在,则直线 的方程为
的方程为 ,由
,由 得
得
设 、
、 ,
, 

∴  ,这与已知相矛盾。
,这与已知相矛盾。
②若直线 的斜率存在,设直线直线
的斜率存在,设直线直线 的斜率为
的斜率为 ,则直线
,则直线 的方程为
的方程为 ,
,
设 、
、 ,
,
联立 ,消元得
,消元得
∴  ,
,
∴  ,
, 
 21世纪教育网
21世纪教育网 

又∵
∴ 
∴ 
化简得
解得
∴ 
∴ 所求直线 的方程为
的方程为 …………………………………12分
…………………………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com