
37.(2009福建卷文)(本小题满分14分)
已知直线 经过椭圆
经过椭圆 21世纪教育网
21世纪教育网 

的左顶点A和上顶点D,椭圆 的右顶点为
的右顶点为 ,点
,点 和椭
和椭
圆 上位于
上位于 轴上方的动点,直线,
轴上方的动点,直线, 与直线
与直线
分别交于 两点。
两点。
(I)求椭圆 的方程;
的方程;
(Ⅱ)求线段MN的长度的最小值;
(Ⅲ)当线段MN的长度最小时,在椭圆 上是否存在这
上是否存在这
样的点 ,使得
,使得 的面积为
的面积为 ?若存在,确定点
?若存在,确定点 的个数,若不存在,说明理由
的个数,若不存在,说明理由

解法一:
(I)由已知得,椭圆 的左顶点为
的左顶点为 上顶点为
上顶点为
故椭圆 的方程为
的方程为
(Ⅱ)直线AS的斜率 显然存在,且
显然存在,且 ,故可设直线
,故可设直线 的方程为
的方程为 ,从而
,从而
由 得
得 0
0
设 则
则 得
得 ,从而
,从而 21世纪教育网
21世纪教育网 

即 又
又
由 得
得

故
又

当且仅当 ,即
,即 时等号成立21世纪教育网
时等号成立21世纪教育网 

 时,线段
时,线段 的长度取最小值
的长度取最小值
(Ⅲ)由(Ⅱ)可知,当 取最小值时,
取最小值时,
此时 的方程为
的方程为
要使椭圆 上存在点
上存在点 ,使得
,使得 的面积等于
的面积等于 ,只须
,只须 到直线
到直线 的距离等于
的距离等于 ,所以
,所以 在平行于
在平行于 且与
且与 距离等于
距离等于 的直线
的直线 上。
上。
设直线
则由 解得
解得 或
或


36.(2009四川卷理)(本小题满分12分)
已知椭圆 的左右焦点分别为
的左右焦点分别为 ,离心率
,离心率 ,右准线方程为
,右准线方程为 。
。
(I)求椭圆的标准方程;
(II)过点 的直线
的直线 与该椭圆交于
与该椭圆交于 两点,且
两点,且 ,求直线
,求直线 的方程。
的方程。
本小题主要考查直线、椭圆、平面向量等基础知识,以及综合运用数学知识解决问题及推理运算能力。
解:(Ⅰ)有条件有 ,解得
,解得 。
。



 。
。
所以,所求椭圆的方程为
 。…………………………………4分
。…………………………………4分
(Ⅱ)由(Ⅰ)知 、
、 。
。
若直线l的斜率不存在,则直线l的方程为x=-1.
将x=-1代入椭圆方程得 。21世纪教育网
。21世纪教育网 

不妨设 、
、 ,
,
 .
.
 ,与题设矛盾。
,与题设矛盾。
 直线l的斜率存在。
直线l的斜率存在。
设直线l的斜率为k,则直线的方程为y=k(x+1)。
设 、
、 ,
,
联立 ,消y得
,消y得 。
。
由根与系数的关系知 ,从而
,从而 ,
,
又 ,
, ,
,
 。
。



 。
。
化简得
解得



35.(2009天津卷理)(本小题满分14分)
以知椭圆 的两个焦点分别为
的两个焦点分别为 ,过点
,过点 的直线与椭圆相交与
的直线与椭圆相交与 两点,且
两点,且 。
。
(1) 求椭圆的离心率;
(2) 求直线AB的斜率;
(3) 设点C与点A关于坐标原点对称,直线 上有一点
上有一点 在
在
 的外接圆上,求
的外接圆上,求 的值
的值
本小题主要考查椭圆的标准方程和几何性质、直线的方程、圆的方程等基础知识,考查用代数方法研究圆锥曲线的性质及数形结合的思想,考查运算能力和推理能力,满分14分
(I)
解:由 //
// 且
且 ,得
,得 ,从而
,从而
整理,得 ,故离心率
,故离心率
(II)
解:由(I)得 ,所以椭圆的方程可写为
,所以椭圆的方程可写为
设直线AB的方程为 ,即
,即 .
.
由已知设 ,则它们的坐标满足方程组
,则它们的坐标满足方程组
消去y整理,得 .
.
依题意,
而  ①
①
 ②
②
由题设知,点B为线段AE的中点,所以
 ③
③
联立①③解得
 ,
, 21世纪教育网
21世纪教育网 

将 代入②中,解得
代入②中,解得 .
.
(III)解法一:由(II)可知
当 时,得
时,得 ,由已知得
,由已知得 .
.
线段 的垂直平分线l的方程为
的垂直平分线l的方程为 直线l与x轴
直线l与x轴
的交点 是
是 外接圆的圆心,因此外接圆的方程为
外接圆的圆心,因此外接圆的方程为 .
.
直线 的方程为
的方程为 ,于是点H(m,n)的坐标满足方程组
,于是点H(m,n)的坐标满足方程组
 , 由
, 由 解得
解得 故
故
当 时,同理可得
时,同理可得 .
.
解法二:由(II)可知
当 时,得
时,得 ,由已知得
,由已知得 21世纪教育网
21世纪教育网 

由椭圆的对称性可知B, ,C三点共线,因为点H(m,n)在
,C三点共线,因为点H(m,n)在 的外接圆上,
的外接圆上,
且 ,所以四边形
,所以四边形 为等腰梯形.
为等腰梯形.
由直线 的方程为
的方程为 ,知点H的坐标为
,知点H的坐标为 .
.
因为 ,所以
,所以 ,解得m=c(舍),或
,解得m=c(舍),或 .
.
则 ,所以
,所以 .
.
当 时同理可得
时同理可得
33.(2009湖南卷理)(本小题满分13分)
在平面直角坐标系xOy中,点P到点F(3,0)的距离的4倍与它到直线x=2的距离的3倍之和记为d,当P点运动时,d恒等于点P的横坐标与18之和

 21世纪教育网
21世纪教育网


(Ⅰ)求点P的轨迹C;
(Ⅱ)设过点F的直线I与轨迹C相交于M,N两点,求线段MN长度的最大值。

解(Ⅰ)设点P的坐标为(x,y),则 3︳x-2︳
3︳x-2︳
由题设
当x>2时,由①得
化简得  21世纪教育网
21世纪教育网


当 时 由①得
时 由①得
化简得
 故点P的轨迹C是椭圆
故点P的轨迹C是椭圆 在直线x=2的右侧部分与抛物线
在直线x=2的右侧部分与抛物线 在直线x=2的左侧部分(包括它与直线x=2的交点)所组成的曲线,参见图1
在直线x=2的左侧部分(包括它与直线x=2的交点)所组成的曲线,参见图1
(Ⅱ)如图2所示,易知直线x=2与 ,
, 的交点都是A(2,
的交点都是A(2, ),
),
B(2, ),直线AF,BF的斜率分别为
),直线AF,BF的斜率分别为 =
= ,
, =
= .
.
当点P在 上时,由②知
上时,由②知
 .
④21世纪教育网
.
④21世纪教育网


当点P在 上时,由③知
上时,由③知 

 ⑤
⑤
若直线l的斜率k存在,则直线l的方程为
(i)当k≤ ,或k≥
,或k≥ ,即k≤-2
,即k≤-2  时,直线I与轨迹C的两个交点M(
时,直线I与轨迹C的两个交点M( ,
, ),N(
),N( ,
, )都在C
)都在C  上,此时由④知
上,此时由④知
∣MF∣= 6 - 
 ∣NF∣= 6 -
∣NF∣= 6 - 



从而∣MN∣= ∣MF∣+ ∣NF∣= (6 - 
 )+ (6 -
)+ (6 - 
 )=12 -
)=12 -  (
(
 +
+ )
)
由 得
得 则
则 ,
, 是这个方程的两根,所以
是这个方程的两根,所以 +
+ =
= *∣MN∣=12 -
*∣MN∣=12 -  (
( +
+ )=12 -
)=12 - 
因为当



当且仅当 时,等号成立。
时,等号成立。
(2)当 时,直线L与轨迹C的两个交点
时,直线L与轨迹C的两个交点 分别在
分别在 上,不妨设点
上,不妨设点 在
在 上,点
上,点 上,则④⑤知,
上,则④⑤知,
设直线AF与椭圆 的另一交点为E
的另一交点为E

所以 。而点A,E都在
。而点A,E都在 上,且
上,且
 有(1)知
有(1)知


若直线 的斜率不存在,则
的斜率不存在,则 =
= =3,此时
=3,此时

综上所述,线段MN长度的最大值为
32.(2009宁夏海南卷文)(本小题满分12分)
已知椭圆 的中心为直角坐标系
的中心为直角坐标系 的原点,焦点在
的原点,焦点在 轴上,它的一个项点到两个
轴上,它的一个项点到两个
焦点的距离分别是7和1
(I)
求椭圆 的方程‘
的方程‘
(II)
若 为椭圆
为椭圆 的动点,
的动点, 为过
为过 且垂直于
且垂直于 轴的直线上的点,
轴的直线上的点,
(e为椭圆C的离心率),求点 的轨迹方程,并说明轨迹是什么曲线。
的轨迹方程,并说明轨迹是什么曲线。
(20)解:
(Ⅰ)设椭圆长半轴长及分别为a,c,由已知得


{ 解得a=4,c=3, 21世纪教育网
解得a=4,c=3, 21世纪教育网 

所以椭圆C的方程为


(Ⅱ)设M(x,y),P(x, ),其中
),其中 由已知得
由已知得

而 ,故
,故 ①
①
由点P在椭圆C上得



代入①式并化简得
所以点M的轨迹方程为 轨迹是两条平行于x轴的线段.
轨迹是两条平行于x轴的线段.


31.(2009湖北卷文)(本小题满分13分)
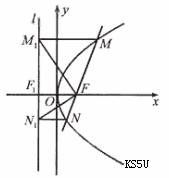
如图,过抛物线y2=2PX(P>0)的焦点F的直线与抛物线相交于M、N两点,自M、N向准线L作垂线,垂足分别为M1、N1
 (Ⅰ)求证:FM1⊥FN1:
(Ⅰ)求证:FM1⊥FN1:
(Ⅱ)记△FMM1、、△FM1N1、△FN N1的面积分别为S1、、S2、,S3,试判断S22=4S1S3是否成立,并证明你的结论。


本小题主要考查抛物线的概念,抛物线的几何性质等平面解析几何的基础知识,考查综合运用数学知识进行推理运算的能力(满分13分)
(1) 证法1:由抛物线的定义得



 2分
2分
 如图,设准线l与x的交点为
如图,设准线l与x的交点为
 21世纪教育网
21世纪教育网 


而
即

故
证法2:依题意,焦点为 准线l的方程为
准线l的方程为
设点M,N的坐标分别为 直线MN的方程为
直线MN的方程为 ,则有
,则有

由 得
得
于是, ,
,
 ,故
,故
(Ⅱ) 成立,证明如下:
成立,证明如下:
证法1:设 ,则由抛物线的定义得
,则由抛物线的定义得
 ,于是
,于是

 21世纪教育网
21世纪教育网 




将 与
与 代入上式化简可得
代入上式化简可得 

 ,此式恒成立。
,此式恒成立。
故 成立。
成立。
证法2:如图,设直线 M的倾角为
M的倾角为 ,
,
则由抛物线的定义得

于是
在 和
和 中,由余弦定理可得
中,由余弦定理可得

由(I)的结论,得

即 ,得证。
,得证。
30.(2009全国卷Ⅰ文)(本小题满分12分)(注意:在试题卷上作答无效)
 如图,已知抛物线
如图,已知抛物线
 与圆
与圆 相交于A、B、C、D四个点。
相交于A、B、C、D四个点。
(Ⅰ)求r的取值范围
(Ⅱ)当四边形ABCD的面积最大时,求对角线AC、BD的交点P的坐标。
解:(Ⅰ)将抛物线 代入圆
代入圆 的方程,消去
的方程,消去 ,整理得
,整理得 .............(1)
.............(1)
抛物线 与圆
与圆 相交于
相交于 、
、 、
、 、
、 四个点的充要条件是:方程(1)有两个不相等的正根
四个点的充要条件是:方程(1)有两个不相等的正根
∴ 即
即 。解这个方程组得
。解这个方程组得
 .
.
(II) 设四个交点的坐标分别为 、
、 、
、 、
、 。
。
则由(I)根据韦达定理有 ,
,
则

令 ,则
,则 下面求
下面求 的最大值。
的最大值。
方法1:由三次均值有:


当且仅当 ,即
,即 时取最大值。经检验此时
时取最大值。经检验此时 满足题意。
满足题意。
法2:设四个交点的坐标分别为 、
、 、
、 、
、
则直线AC、BD的方程分别为

解得点P的坐标为 。
。
设 ,由
,由 及(Ⅰ)得
及(Ⅰ)得

由于四边形ABCD为等腰梯形,因而其面积
则 将
将 ,
, 代入上式,并令
代入上式,并令 ,等
,等
 ,
,
∴ ,
,
令 得
得 ,或
,或 (舍去)
(舍去)
当 时,
时, ;当
;当 时
时 ;当
;当 时,
时,
故当且仅当 时,
时, 有最大值,即四边形ABCD的面积最大,故所求的点P的坐标为
有最大值,即四边形ABCD的面积最大,故所求的点P的坐标为 。
。

(Ⅱ)设直线AB的方程为 由题意知
由题意知 21世纪教育网
21世纪教育网 

由{ 得A点的坐标为
得A点的坐标为
由{ 得B点的坐标为
得B点的坐标为
由 得P点的坐标为
得P点的坐标为
将P点坐标代入
设Q为直线AB与y轴的交点,则Q点的坐标为(0,m).

=
以下同解答一.
29.(2009四川卷文)(本小题满分12分)


已知椭圆 的左、右焦点分别为
的左、右焦点分别为 ,离心率
,离心率 ,右准线方程为
,右准线方程为 。
。
(I)求椭圆的标准方程;
(II)过点 的直线
的直线 与该椭圆交于
与该椭圆交于 两点,且
两点,且 ,求直线
,求直线 的方程。
的方程。
[解析](I)由已知得 ,解得
,解得


∴ 
∴ 所求椭圆的方程为 …………………………………4分
…………………………………4分
(II)由(I)得 、
、
①若直线 的斜率不存在,则直线
的斜率不存在,则直线 的方程为
的方程为 ,由
,由 得
得
设 、
、 ,
, 

∴  ,这与已知相矛盾。
,这与已知相矛盾。
②若直线 的斜率存在,设直线直线
的斜率存在,设直线直线 的斜率为
的斜率为 ,则直线
,则直线 的方程为
的方程为 ,
,
设 、
、 ,
,
联立 ,消元得
,消元得
∴  ,21世纪教育网
,21世纪教育网 

∴  ,
, 

又∵
∴ 
∴ 
化简得
解得
∴ 
∴ 所求直线 的方程为
的方程为 …………………………………12分
…………………………………12分
∴
由 得
得 ∴双曲线C的方程为
∴双曲线C的方程为
(Ⅱ)由(Ⅰ)知双曲线C的两条渐近线方程为
设
由 得P点的坐标为
得P点的坐标为
将P点坐标代入 化简得
化简得
设∠AOB
又

记
由
当 时,△AOB的面积取得最小值2,当
时,△AOB的面积取得最小值2,当 时,△AOB的面积取得最大值
时,△AOB的面积取得最大值 ∴△AOB面积的取值范围是
∴△AOB面积的取值范围是
28.(本小题满分14分)
已知双曲线C的方程为 21世纪教育网
21世纪教育网 

离心率 顶点到渐近线的距离为
顶点到渐近线的距离为
(Ⅰ)求双曲线C的方程;
(Ⅱ)如图,P是双曲线C上一点,A,B两点在双曲线C的两条渐近线上,且分别位于第一,二象限.若 求△AOB面积的取值范围.
求△AOB面积的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com