
6.(2009浙江文)已知 是实数,则函数
是实数,则函数 的图象不可能是( )21世纪教育网
的图象不可能是( )21世纪教育网 

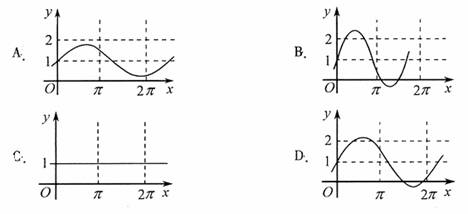
D [命题意图]此题是一个考查三角函数图象的问题,但考查的知识点因含有参数而丰富,结合图形考查使得所考查的问题形象而富有深度.
[解析]对于振幅大于1时,三角函数的周期为 ,而D不符合要求,它的振幅大于1,但周期反而大于了
,而D不符合要求,它的振幅大于1,但周期反而大于了 .
.
5.(2009浙江理)已知 是实数,则函数
是实数,则函数 的图象不可能是 ( )
的图象不可能是 ( )

答案:D
[解析]对于振幅大于1时,三角函数的周期为 ,而D不符合要求,它的振幅大于1,但周期反而大于了
,而D不符合要求,它的振幅大于1,但周期反而大于了 .
.
4.(2009全国卷Ⅰ理)若 ,则函数
,则函数 的最大值为
。
的最大值为
。
解:令
 ,
, 




3.(2009全国卷Ⅰ理)如果函数 的图像关于点
的图像关于点 中心对称,那么
中心对称,那么 的最小值为(C)(A)
的最小值为(C)(A) (B)
(B) (C)
(C) (D)
(D) 

 解:
解:  函数
函数 的图像关于点
的图像关于点 中心对称
中心对称 


 由此易得
由此易得 .故选C
.故选C
2.(2009年广东卷文)函数 是
是
A.最小正周期为 的奇函数 B. 最小正周期为
的奇函数 B. 最小正周期为 的偶函数
的偶函数
C. 最小正周期为 的奇函数 D. 最小正周期为
的奇函数 D. 最小正周期为 的偶函数
的偶函数
[答案]A
[解析]因为 为奇函数,
为奇函数, ,所以选A.
,所以选A.
1.(2009年广东卷文)已知 中,
中, 的对边分别为
的对边分别为 若
若 且
且 ,则
,则
A.2 B.4+ C.4-
C.4- D.
D.
[答案]A
[解析]
由 可知,
可知, ,所以
,所以 ,
,
由正弦定理得 ,故选A
,故选A
41.(2009重庆卷文)(本小题满分12分,(Ⅰ)问5分,(Ⅱ)问7分)
已知以原点 为中心的双曲线的一条准线方程为
为中心的双曲线的一条准线方程为 ,离心率
,离心率 .
.
(Ⅰ)求该双曲线的方程;
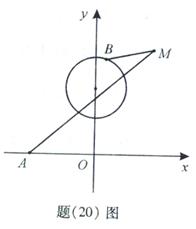
(Ⅱ)如题(20)图,点 的坐标为
的坐标为 ,
, 是圆
是圆 上的点,点
上的点,点 在双曲线右支上,求
在双曲线右支上,求 的最小值,并求此时
的最小值,并求此时 点的坐标;
点的坐标; 
 21世纪教育网
21世纪教育网 

解:(Ⅰ)由题意可知,双曲线的焦点在 轴上,故可设双曲线的方程为
轴上,故可设双曲线的方程为 ,设
,设 ,由准线方程为
,由准线方程为 得
得 ,由
,由
得 解得
解得 从而
从而 ,
, 该双曲线的方程为
该双曲线的方程为 ;
;
(Ⅱ)设点D的坐标为 ,则点A、D为双曲线的焦点,
,则点A、D为双曲线的焦点,
所以 ,
,
 是圆
是圆 上的点,其圆心为
上的点,其圆心为 ,半径为1,故
,半径为1,故 从而
从而
当 在线段CD上时取等号,此时
在线段CD上时取等号,此时 的最小值为
的最小值为
 直线CD的方程为
直线CD的方程为 ,因点M在双曲线右支上,故
,因点M在双曲线右支上,故
由方程组 解得
解得
所以 点的坐标为
点的坐标为 ;
; 
 21世纪教育网
21世纪教育网 

40.(2009重庆卷理)(本小题满分12分,(Ⅰ)问5分,(Ⅱ)问7分)
已知以原点 为中心的椭圆的一条准线方程为
为中心的椭圆的一条准线方程为 ,离心率
,离心率 ,
, 是椭圆上的动点.
是椭圆上的动点.
(Ⅰ)若 的坐标分别是
的坐标分别是 ,求
,求 的最大值;
的最大值;
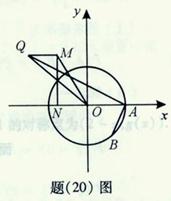
(Ⅱ)如题(20)图,点 的坐标为
的坐标为 ,
, 是圆
是圆 上的点,
上的点, 是点
是点 在
在 轴上的射影,点
轴上的射影,点 满足条件:
满足条件: ,
, .求线段
.求线段 的中点
的中点 的轨迹方程;
的轨迹方程;
 21世纪教育网
21世纪教育网 

(20)(本小题12分)
解:(Ⅰ)由题设条件知焦点在y轴上,故设椭圆方程为 (a >b> 0 ).
(a >b> 0 ).
设 ,由准线方程
,由准线方程 得.由
得.由 得
得 ,解得 a = 2 ,c =
,解得 a = 2 ,c =  ,从而 b = 1,椭圆方程为
,从而 b = 1,椭圆方程为 .
.
又易知C,D两点是椭圆 的焦点,所以,
的焦点,所以,
从而 ,当且仅当
,当且仅当 ,即点M的坐标为
,即点M的坐标为 时上式取等号,
时上式取等号, 的最大值为4 . 21世纪教育网
的最大值为4 . 21世纪教育网 

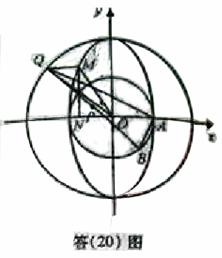
(II)如图(20)图,设
 .因为
.因为 ,故
,故

 ①
①
因为

所以  . ②
. ②
记P点的坐标为 ,因为P是BQ的中点
,因为P是BQ的中点
所以 
由因为  ,结合①,②得
,结合①,②得
 21世纪教育网
21世纪教育网 




故动点P的估计方程为

39.(2009上海卷文)(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分4分,第3小题满分8分.
已知双曲线C的中心是原点,右焦点为F ,一条渐近线m:
,一条渐近线m: ,设过点A
,设过点A 的直线l的方向向量
的直线l的方向向量 。
。
(1) 求双曲线C的方程;
(2) 若过原点的直线 ,且a与l的距离为
,且a与l的距离为 ,求K的值;
,求K的值;
(3) 证明:当 时,在双曲线C的右支上不存在点Q,使之到直线l的距离为
时,在双曲线C的右支上不存在点Q,使之到直线l的距离为 .
.
[解](1)设双曲线 的方程为
的方程为
 ,解额
,解额 双曲线
双曲线 的方程为
的方程为
(2)直线 ,直线
,直线
由题意,得 ,解得
,解得
(3)[证法一]设过原点且平行于 的直线
的直线
则直线 与
与 的距离
的距离 当
当 时,
时, 21世纪教育网
21世纪教育网 

又双曲线 的渐近线为
的渐近线为



 双曲线
双曲线 的右支在直线
的右支在直线 的右下方,
的右下方,
 双曲线
双曲线 右支上的任意点到直线
右支上的任意点到直线 的距离大于
的距离大于 。
。
故在双曲线 的右支上不存在点
的右支上不存在点 ,使之到直线
,使之到直线 的距离为
的距离为
[证法二]假设双曲线 右支上存在点
右支上存在点 到直线
到直线 的距离为
的距离为 ,
,
则
由(1)得
设 ,
,
当 时,
时, ;
;

将 代入(2)得
代入(2)得
 ,
, 


 方程
方程 不存在正根,即假设不成立,
不存在正根,即假设不成立,
故在双曲线 的右支上不存在点
的右支上不存在点 ,使之到直线
,使之到直线 的距离为
的距离为 21世纪教育网
21世纪教育网 

38.(2009年上海卷理)(本题满分16分)本题共有2个小题,第1小题满分8分,第2小题满分8分。
已知双曲线 设过点
设过点 的直线l的方向向量
的直线l的方向向量


(1) 当直线l与双曲线C的一条渐近线m平行时,求直线l的方程及l与m的距离;
(2)
证明:当 >
> 时,在双曲线C的右支上不存在点Q,使之到直线l的距离为
时,在双曲线C的右支上不存在点Q,使之到直线l的距离为 。
。
解:(1)双曲线C的渐近线
 直线l的方程
直线l的方程 ………………..6分
………………..6分


直线l与m的距离 ……….8分
……….8分 
(2)设过原点且平行与l的直线
则直线l与b的距离
当


又双曲线C的渐近线为

 双曲线C的右支在直线b的右下方,
双曲线C的右支在直线b的右下方,
 双曲线
双曲线 右支上的任意点到直线
右支上的任意点到直线 的距离为
的距离为 。
。
故在双曲线 的右支上不存在点
的右支上不存在点 ,使之到直线
,使之到直线 的距离为
的距离为 。
。
[ 证法二] 双曲线 的右支上存在点
的右支上存在点
 到直线
到直线 的距离为
的距离为 ,
,
则
由(1)得 ,
, 
设

 21世纪教育网
21世纪教育网


当 ,
,

 0………………………………..13分
0………………………………..13分
将 代入(2)得
代入(2)得 (*)
(*)

 方程(*)不存在正根,即假设不成立
方程(*)不存在正根,即假设不成立


故在双曲线C的右支上不存在Q,使之到直线l 的距离为 …………….16分
…………….16分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com