5. 设定义域为R的函数，则关于的方程有7个不同实数解的充要条件是 　　 ( )

A. 且　 B. 且　 C. 且　 D. 且

4. 若函数，则该函数在上是　　　　　　 ( )

　　 A. 单调递减无最小值　　　　 　　　　 B. 单调递减有最小值

　　 C. 单调递增无最大值　　　　 　　　　 D. 单调递增有最大值

3. 设函数的定义域为，有下列三个命题：

(1)若存在常数，使得对任意，有，则是函数的最大值；

(2)若存在，使得对任意，且，有，则是函数的最大值；

(3)若存在，使得对任意，有，则是函数的最大值.这些命题中，真命题的个数是　 (　 )

　　 A. 0个　　　　　　 B. 1个　　　　　　 C. 2个　　　　　　 D. 3个

2. 函数　　　　 ( )

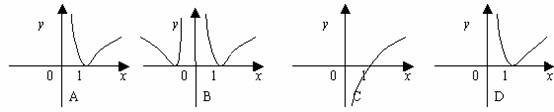
1. 函数y=|log_­2x|的图象是　　　　　　　　　　　　　　　　 ( )

　

3、复习建议

(1)认真落实本章的每个知识点，注意揭示概念的数学本质

①函数的表示方法除解析法外还有列表法、图象法，函数的实质是客观世界中量的变化的依存关系；

②中学数学中的“正、反比例函数，一次、二次函数，指数、对数函数，三角函数”称为基本初等函数，其余的函数的解析式都是由这些基本初等函数的解析式形成的. 要把基本初等函数的图象和性质联系起来，并且理解记忆；

③掌握函数单调性和奇偶性的一般判定方法，并能联系其相应的函数的图象特征，加强对函数单调性和奇偶性应用的训练；

④注意函数图象的变换：平移变换、伸缩变换、对称变换等；

⑤掌握复合函数的定义域、值域、单调性、奇偶性；

(2)以函数知识为依托，渗透基本数学思想和方法

①数形结合的思想，即要利用函数的图象解决问题；

②建模方法，要能在实际问题中引进变量，建立函数模型，进而提高解决应用题的能力，培养函数的应用意识。

(3)深刻理解函数的概念，加强与各章知识的横向联系

　　 要与时俱进地认识本章内容的“双基”，准确、深刻地理解函数的概念，才能正确、灵活地加以运用，养成自觉地运用函数观点思考和处理问题的习惯；高考范围没有的内容例如指数不等式(方程)、对数不等式(方程)等不再作深入研究；导数可用来证明函数的单调性，求函数的最大值和最小值，并启发学生建构更加完整的函数知识结构。

所谓函数思想，实质上是将问题放到动态背景上去考虑，利用函数观点可以从较高的角度处理式、方程、不等式、数列、曲线等问题。

[典型例题]

例1. 设是R上的偶函数，且在区间上递增，若成立，求a的取值范围。

解：

故为所求。

例2. 关于x的不等式2·3^2x–3^x+a²–a–3＞0，当0≤x≤1时恒成立，则实数a的取值范围为　　　 .

解：设t=3^x，则t∈［1,3］，原不等式可化为a²–a–3＞–2t²+t,t∈［1,3］.

等价于a²–a–3大于f(t)=–2t²+t在［1,3］上的最大值.

答案：(–∞,–1)∪(2,+∞)

例3. 设是定义在上的奇函数，的图象与的图象关于直线对称，而当时，(c为常数)。

(1)求的表达式；

(2)对于任意，且，求证：；

(3)对于任意，且，求证：1.

解：(1)设g(x)上点与f(x)上点P(x，y)对应，

∴　 ；∵在g(x)图象上

∴

∵g(x)定义域为x∈[2,3]，而f(x)的图象与g(x)的图象关于直线x=1对称，

所以，上述解析式是f(x)在[–1，0]上的解析式

∵f(x)是定义在[–1,1]上的奇函数，∴f(0)=0，∴c=–4　

所以，当x∈[0，1]时，–x∈[–1，0]，f(x)=–f(–x)=–　

所以

(2)当x∈[0，1]时，

∵，∴，所以

(3)∵，∴

∴，∴

即

例4. 设函数f(x)的定义域关于原点对称，且满足① ②存在正常数a，使f(a) = 1，求证：(1)f(x)为奇函数；(2)f(x)为周期函数，且一个周期为4a。

证明：(1)令x =x₁ - x₂

则f( - x) = f ( x₂ - x₁)=

= －f (x₁ －x₂ )= －f (x)，∴f (x)为奇函数。

(2)∵f( x+a ) = f[x － ( －a ) ]=

∴f (x+2a )=

∴f ( x+4a)==f (x)

　∴f (x)是以4a为周期的周期函数。

例5. 已知函数f(x)=log_m

(1)若f(x)的定义域为，(β＞α＞0)，判断f(x)在定义域上的增减性，并加以说明；

(2)当0＜m＜1时，使f(x)的值域为的定义域区间为

(β＞α＞0)是否存在？请说明理由.

解：(1)x＜–3或x＞3.

∵f(x)定义域为,∴α＞3

设β≥x₁＞x₂≥α，有

当0＜m＜1时，f(x)为减函数，当m＞1时，f(x)为增函数.

(2)若f(x)在上的值域为

∵0＜m＜1, f(x)为减函数.

∴

即

即α,β为方程mx²+(2m–1)x–3(m–1)=0的大于3的两个根

∴　 ∴0＜m＜

故当0＜m＜时，满足题意条件的m存在.

例6. 已知函数f(x)=x²–(m+1)x+m(m∈R)

(1)若tanA,tanB是方程f(x)+4=0的两个实根，A、B是锐角三角形ABC的两个内角.求证：m≥5;

(2)对任意实数α,恒有f(2+cosα)≤0，证明m≥3;

(3)在(2)的条件下，若函数f(sinα)的最大值是8，求m.

解：(1)证明：f(x)+4=0即x²–(m+1)x+m+4=0.依题意：

　 又A、B锐角为三角形ABC内两内角

∴＜A+B＜π

∴tan(A+B)＜0，即

∴∴m≥5

(2)证明：∵f(x)=(x–1)(x–m)

又–1≤cosα≤1，∴1≤2+cosα≤3，恒有f(2+cosα)≤0

即1≤x≤3时，恒有f(x)≤0即(x–1)(x–m)≤0

∴m≥x但x_max=3，∴m≥x_max=3

(3)解：∵f(sinα)=sin²α–(m+1)sinα+m=

且≥2,∴当sinα=–1时，f(sinα)有最大值8.

即1+(m+1)+m=8，∴m=3

例7. 已知函数的定义域为实数集。(1)求实数m的所有允许值组成的集合M；(2)求证：对所有，恒有 。

证明(1)∵的定义域为实数集

(2)令

例8. 设=，(a>0,a≠1)，求证：(1)过函数y=f(x)图象上任意两点直线的斜率恒大于0；(2)f(3)>3。

解：(1)令t=，则x=，f(x)= 　(t∈R)

∴f(x)= 　(x∈R)

设，f()－f()=

(1)a>1时，…，f()<f()，∴f(x)在(－∞,+∞)上单调递增

(2)0<a<1时，…，f()<f()，∴f(x)在(－∞,+∞)上单调递增

∴<时，恒有f()<f()，∴k=>0

(2)f(3)=

∵a>0，a≠1　 ∴　 ∴上述不等式不能取等号，∴f(3)>3

例9. 已知函数f(x)=lg(的定义域为(0，+∞)，问是否存在这样的a,b，使f(x)恰在(1，+∞)上取正值，且f(3)=lg4，若存在，求出a,b的值，若不存在，说明理由。

解：由，得，∵a>1>b>0，∴>1，∴x>log

又f(x)定义域为(0，+∞)，∴log=0，k=1，∴f(x)=lg

设0<，，∵a>1>b>0，∴a< a，－b< b

∴0< a－b< a－ b，∴0<<1，∴lg<0

∴，∴f(x)在(0，+∞)上是增函数

∴x(1,+∞)时，必有f(x)>f(1)=lg(a－b)

∵f(x)在(1，+∞)上取正值，∴lg(a－b)=0　 a－b=1　 (1)

又f(3)=lg4　 ∴lg=lg4， =4　　　 (2)

解(1)(2)得：，b=，即有在，b=时满足题设条件。

例10. 设二次函数f(x)= ax² +bx+c (a>0且b≠0)。

(1)已知|f(0)|=|f(1)|=|f(-1)|=1，试求f(x)的解析式和f(x)的最小值；

(2)已知f(x)的对称轴方程是x=1，当f(x)的图象在x轴上截得的弦长不小于2时，试求a, b, c满足的条件；

(3)已知|b|<a, |f(0)|1, |f(-1)|1, |f(1)|1，当|x|1时，证明：|f(x)|

解：(1)由|f(0)|=|f(1)|=|f(-1)|知|c|=1，|a+b+c|=1，|a-b+c|=1

∴(a+b+c)²=(a-b+c)²即4(a+c)b=0

∵b≠0　 ∴a+c=0，即：a=-c

又∵a>0　 ∴a=1 c=-1　 此时b=+1　 ∴f(x)=x² + x-1

于是 f(x)=(x + )²　　 ∴[f(x)]

　　 (2)依题意即b=-2a，∵a>0且b≠0　 ∴b<0

令f(x)=0的两根为x₁，x₂，则函数y=f(x)的图象与x轴的两个交点为(x₁，0)，(x₂，0)

且，满足题设的充要条件是

∴a>0，c0，b<0且b=－2a为所求

　　 (3)方法1：

　　 ∵|2b|=|(a+b+c)-(a-b+c)|<|a+b+c|+|a-b+c|<2　 ∴|b|1　 又|b||a|　 ∴1　

又|c|=|f(0)|1　 又|f(

而f(x)所示开口向上的抛物线且|x|<1，则|f(x)|的最大值应在x=1或x=-1或x=-时取到，因|f(-1)|<1, |f(1)|1, |f(-)|　 故|f(x)|得证。

　　 方法2：

令f(x)=uf(1)+vf(-1)+(1-u-v)f(0) 则f(x)=(a+b+c)u+(a-b+c)v+(1-u-v)c

ax² +bx+c=a(u+v)+b(u-v)+c

∴　　

∴f(x)=

而|f(1)| 1, |f(-1)|1, |f(0)|1

∴<　 x∈[-1, 1]

　　 =|x|·==

综上，当|f(0)|1, |f (-1)|1, |f(-1)|1, |x|1时，|f(x)|

方法3：我们可以把，和当成两个独立条件，先用和来表示.

∵ ,

∴ ,

∴ .

∴ 当时，，所以，根据绝对值不等式的性质可得：

，，

∴

综上，问题获证.

[模拟试题]

2、热点分析

　　 函数是高考数学的重点内容之一，函数的观点和思想方法贯穿整个高中数学的全过程，包括解决几何问题。在近几年的高考试卷中，选择题、填空题、解答题三种题型中每年都有函数试题，而且常考常新。以基本函数为背景的应用题和综合题是高考命题的新趋势。

　　 考试热点：①考查函数的表示法、定义域、值域、单调性、奇偶性和函数的图象。②函数与方程、不等式、数列是相互关联的概念，通过对实际问题的抽象分析，建立相应的函数模型并用来解决问题，是考试的热点。

③考查运用函数的思想来观察问题、分析问题和解决问题，渗透数形结合和分类讨论的基本数学思想。

1、高考要求

(1)了解映射的概念，理解函数的概念.

(2)了解函数的单调性和奇偶性的概念，掌握判断一些简单函数的单调性和奇偶性的方法，并能利用函数的性质简化函数图像的绘制过程.

(3)理解分数指数的概念，掌握有理指数幂的运算性质. 掌握指数函数的概念、图像和性质.

(4)理解对数的概念，掌握对数的运算性质. 掌握对数函数的概念、图像和性质.

(5)能够运用函数的性质、指数函数和对数函数的性质解决某些简单的实际问题.

专题：函数

(四)说明书式

　福建 考生

　产品名：心灵牌天平

　测量物：有待认知的事物

　构件：灵魂骨架一个，心灵托盘两件，“亲疏关系”、“眼观”、“耳听”、“心品”四套砝码各一

　精确度：因人而异！

　使用方法细则及示例：

　(1)遵守左盘放物、右盘放码的总原则；

　(2)若只放“亲疏关系”码则测量必不准！下示例以作警示：

　①古有贤人形貌昳丽，窥镜自视，自知不若另一男子徐公者。贤人问其妻、其妾、其客：“我与徐公，孰美？”其妻曰：“徐公不若君之美也！”其妾、其客皆曰：“群美甚，徐公何能及君也！”妻妾客皆以“亲疏关系”码去测量此美男子，从而导致结果与事实大相径庭。该贤人喟叹不已。

　②我国改革开放之初，经济衰败，如何复兴经济、重振国威成为领导人的首要任务！有识之士提出发展部分特区，吸收外资，引他山活水以浚我处泉源。谁料此声一出当即惨遭镇压，大部分人以“亲疏关系”草率否定资本主义的优点。好在高瞻远瞩的邓总设计师提出改革开放、大胆吸收外资，从而使复兴伟业蒸蒸日上。

　③非典病毒，肆虐神州，但与普通肺炎的6%~7%的死亡率比起来，非典3%-4%则小了许多，那么为何这冠状病毒会引起如此恐慌呢？因为人们用“亲疏关系”去测量非典，一致认为“陌生”即是“恐怖”的代名词。非典一事证明该测量的不准确性。

　④张国荣，这个被许多明星和影迷亲切地称为“哥哥”的人，有谁料到他会跳楼自杀呢？有谁真正了解他，认知他呢？“亲疏关系”码这一次又测错了！

　(3)测量事物应该四码皆用，先放“眼观”、“耳听”两码，从外观表像入手，再放“亲疏关系”码，最后别忘了最重要的“心品”码！唯有知其心才能识其人。现举例说明：

　①韩国前任总统金大中兢兢业业，其二子却贪财受贿。金大中经过认真测量，将其子送上法庭，受到国人尊敬，传为美谈。

　②将您正确测量的结果填于此

　(4)本产品随测量的正确率的提高而提升精确度！

　(5)使用年限：从出生至死亡。　

　简评：作者思维活跃，采用变异的说明文形式表现深刻的主题，的确别具新意。形式的新颖使文章在结构安排、内容的选择上有了广阔的空间，借助说明书的外衣，巧妙地谈论了我们在认识事物和处理问题的时候，如果只重视亲疏关系，必然导致认识的不准确，语言诙谐幽默。