
4.实数与向量的积
(1)实数λ与向量 的积:①是个向量;②模等于
的积:①是个向量;②模等于 ③方向λ>0时与
③方向λ>0时与 同向,λ<0时与
同向,λ<0时与 反向.
反向.
(2)数乘向量满足交换律、结合律与分配律。
3.向量的减法
(1)相反向量:
关于相反向量有: ① =
= ; ②
; ② +(
+( )=(
)=( )+
)+ =
= ;
;
③若 、
、 是互为相反向量,则
是互为相反向量,则 =
= ,
, =
= ,
, +
+ =
= 。
。
(2)向量减法:向量 加上
加上 的相反向量叫做
的相反向量叫做 与
与 的差,记作:
的差,记作: 。求两个向量差的运算,叫做向量的减法。
。求两个向量差的运算,叫做向量的减法。
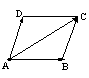
如上图 表示为从
表示为从 的终点指向
的终点指向 的终点的向量(
的终点的向量( 、
、 有共同起点)。
有共同起点)。
(3)温馨提示:①用平行四边形法则时,两个已知向量是要共始点的,和向量与差向量分别是两条对角线,注意方向。
②三角形法则的特点是“顺次首尾相接”由此可知,封闭折线的向量和为零.
差向量是从减向量的终点指向被减向量的终点。
2.向量加法: 设 ,
,
(1)求两个向量和的运算叫做向量的加法,向量加法按“平行四边形法则”或“三角形法则”进行。
 如图
如图  +
+ =
= =
= 。 或
。 或  +
+ =
=
规定: ;
;
(2) 向量加法满足交换律与结合律;
1.向量的有关概念
(1)向量:既有大小又有方向的量.
可用有向线段表示.记作: …或
…或 …等;向量的长度即向量的模记作|
…等;向量的长度即向量的模记作| |。
|。
(2)零向量: 其方向:
(3)单位向量: 单位向量不唯一.
(4)平行向量(共线向量):方向相同或相反方向相同或相反.
规定: 与任意向量平行。
与任意向量平行。
(5)相等向量:长度相等且方向相同.
1理解向量的概念,掌握向量的几何表示,了解共线向量的概念
2掌握向量的加法和减法
3掌握实数与向量的积;理解两个向量共线的充要条件
4.函数定义域为 ,当
,当 时,
时,

令 ,解得
,解得 ,∴
,∴ ,
,
又 ,∴
,∴
说明:对于闭区间 上的连续函数,如果在相应开区间
上的连续函数,如果在相应开区间 内可导,求
内可导,求 上最值可简化过程,即直接将极值点与端点的函数值比较,即可判定最大(或最小)的函数值,就是最大(或最小)值.解决这类问题,运算欠准确是普遍存在的一个突出问题,反映出运算能力上的差距.运算的准确要依靠运算方法的合理与简捷,需要有效的检验手段,只有全方位的“综合治理”才能在坚实的基础上形成运算能力,解决运算不准确的弊病.
上最值可简化过程,即直接将极值点与端点的函数值比较,即可判定最大(或最小)的函数值,就是最大(或最小)值.解决这类问题,运算欠准确是普遍存在的一个突出问题,反映出运算能力上的差距.运算的准确要依靠运算方法的合理与简捷,需要有效的检验手段,只有全方位的“综合治理”才能在坚实的基础上形成运算能力,解决运算不准确的弊病.
求两变量乘积的最大值
例 已知 为正实数,且满足关系式
为正实数,且满足关系式 ,求
,求 的最大值.
的最大值.
分析:题中有两个变量x和y,首先应选择一个主要变量,将 表示为某一变量(x或y或其它变量)的函数关系,实现问题的转化,同时根据题设条件确定变量的取值范围,再利用导数(或均值不等式等)求函数的最大值.
表示为某一变量(x或y或其它变量)的函数关系,实现问题的转化,同时根据题设条件确定变量的取值范围,再利用导数(或均值不等式等)求函数的最大值.
解:解法一: ,
,
∴ .
.
由 解得
解得 .
.
设
当 时,
时,
 .
.
令 ,得
,得 或
或 (舍).
(舍).
∴ ,又
,又 ,∴函数
,∴函数 的最大值为
的最大值为 .
.
即 的最大值为
的最大值为 .
.
解法二:由 得
得 ,
,
设 ,
,
∴ ,设
,设 ,
,
则

令 ,得
,得 或
或 .
.
 ,此时
,此时
∴
即当 时,
时,
说明:进行一题多解训练,是一种打开思路,激发思维,巩固基础,沟通联系的重要途径,但要明确解决问题的策略、指向和思考方法,需要抓住问题的本质,领悟真谛,巧施转化,方可快捷地与熟悉的问题接轨,在实现转化的过程中,关键是要注意变量的取值范围必须满足题设条件,以免解题陷于困境,功亏一篑.
3. .
.
令 ,即
,即 ,解得
,解得
当 时,
时, ,当
,当 时,
时, .
.
∴函数 在点
在点 处取得极小值,也是最小值为
处取得极小值,也是最小值为
 即
即 .
.
2. ,令
,令 ,得
,得 ,
,
∴ ,
,
又 .
.
∴
4. .
.
分析:函数 在给定区间上连续可导,必有最大值和最小值,因此,在求闭区间
在给定区间上连续可导,必有最大值和最小值,因此,在求闭区间 上函数的最值时,只需求出函数
上函数的最值时,只需求出函数 在开区间
在开区间 内的极值,然后与端点处函数值进行比较即可.
内的极值,然后与端点处函数值进行比较即可.
解:1. ,令
,令 ,得
,得 ,
,
∴ .又
.又
∴
3.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com