
3、理解图象所反映的化学意义;
2、坐标原点在纵轴和横轴上所表示的数值;
1、要懂得纵轴、横轴所表示的化学意义;

当x>5时,原不等式可化为
x-5-(2x+3)<1,
解之得x>-9,所以x>5.

说明:在含有绝对值的不等式中,“去绝对值”是基本策略.
例13 解不等式|2x-1|>|2x-3|.
分析 本题也可采取前一题的方法:采取用零点分区间讨论去掉绝

之,则更显得流畅,简捷.
解 原不等式同解于
(2x-1)2>(2x-3)2,
即4x2-4x+1>4x2-12x+9,
即8x>8,得x>1.
所以原不等式的解集为{x|x>1}.
说明:本题中,如果把2x当作数轴上的动坐标,则|2x-1|>|2x-3|表示2x到1的距离大于2x到3的距离,则2x应当在2的右边,从而2x>2即x>1.
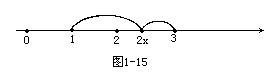
22.(理)已知函数 ,
,
(1)讨论 的奇偶性与单调性;
的奇偶性与单调性;
(2)若不等式 的解集为
的解集为 的值;
的值;
(3)求 的反函数
的反函数 ;
;
(4)若 ,解关于
,解关于 的不等式
的不等式 R).
R).
(文) 函数 的定义域为
的定义域为 (
( 为实数).
为实数).
(1)当 时,求函数
时,求函数 的值域;
的值域;
(2)若函数 在定义域上是减函数,求
在定义域上是减函数,求 的取值范围;
的取值范围;
.
21.函数 是定义在R上的奇函数,当
是定义在R上的奇函数,当 ,
,
(1)求x<0时, 的解析式;
的解析式;
(2)问是否存在这样的正数a,b,当 的值域为
的值域为 ?若存在,求出所有的a,b的值;若不存在说明理由.
?若存在,求出所有的a,b的值;若不存在说明理由.
20.有两个煤矿用汽车供应三个城镇的用煤,第一个煤矿月产煤120万吨,第二个煤矿月产煤200万吨. 第一个城镇每月用煤90万吨,第二个城镇每月用煤150万吨,第三个城镇每月用煤80万吨,又知第一个煤矿与三城镇的中心供应站的距离分别为20公里、10公里和12公里;第二个煤矿与三个城城镇的中心站的距离分别为8公里、16公里和30公里,问怎样调配煤才能使总的运输费用最少?
19.已知函数 图象与函数
图象与函数 的图象关于点A(0,1)对称。(1)求
的图象关于点A(0,1)对称。(1)求 的解析式;(2)若
的解析式;(2)若 ,且
,且 在区间
在区间 上为减函数,求实数
上为减函数,求实数 的取值范围。
的取值范围。
18.设 ,若
,若 ,求证:(1)
,求证:(1) 且
且 ; (2)方程
; (2)方程 在(0,1)内有两个实根。
在(0,1)内有两个实根。
17.已知f(x)是对数函数,f( )+f(
)+f( )=1,求f(
)=1,求f( )的值。
)的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com