
12.(2009天津卷理)设变量x,y满足约束条件: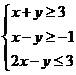 .则目标函数z=2x+3y的最小值为
.则目标函数z=2x+3y的最小值为
(A)6 (B)7 (C)8 (D)23
[考点定位]本小考查简单的线性规划,基础题。
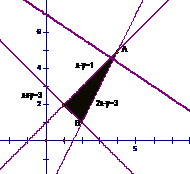
解析:画出不等式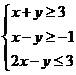 表示的可行域,如右图,
表示的可行域,如右图, 

让目标函数表示直线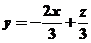 在可行域上平移,知在点B自目标函数取到最小值,解方程组
在可行域上平移,知在点B自目标函数取到最小值,解方程组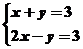 得
得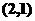 ,所以
,所以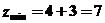 ,故选择B。
,故选择B。 

11.(2009湖南卷理)已知D是由不等式组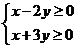 ,所确定的平面区域,则圆
,所确定的平面区域,则圆 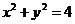 在区域D内
在区域D内
的弧长为 [ B]
A 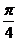 B
B C
C  D
D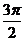



[答案]:B
[解析]解析如图示,图中阴影部分所在圆心角所对弧长即为所求,易知图中两直线的斜率分别是
 ,所以圆心角
,所以圆心角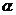 即为两直线的所成夹角,所以
即为两直线的所成夹角,所以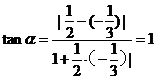 ,所以
,所以 ,而圆的半径是2,所以弧长是
,而圆的半径是2,所以弧长是 ,故选B现。
,故选B现。
10.(2009宁夏海南卷文)设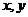 满足
满足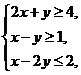 则
则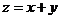
(A)有最小值2,最大值3 (B)有最小值2,无最大值
(C)有最大值3,无最小值
(D)既无最小值,也无最大值 

[答案]B
[解析]画出不等式表示的平面区域,如右图,由z=x+y,得y=-x+z,令z=0,画出y=-x的图象,当它的平行线经过A(2,0)时,z取得最小值,最小值为:z=2,无最大值,故选.B
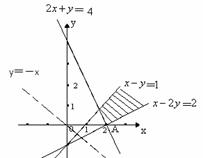
9.(2009宁夏海南卷理)设x,y满足
(A)有最小值2,最大值3 (B)有最小值2,无最大值
(C)有最大值3,无最小值 (D)既无最小值,也无最大值
解析:画出可行域可知,当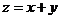 过点(2,0)时,
过点(2,0)时,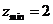 ,但无最大值。选B.
,但无最大值。选B.
8.(2009湖南卷文)若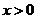 ,则
,则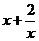 的最小值为
的最小值为  .
.
解: 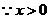
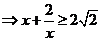 ,当且仅当
,当且仅当 时取等号.
时取等号.
7.(2009山东卷理)设x,y满足约束条件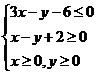 ,
,
若目标函数z=ax+by(a>0,b>0)的值是最大值为12,
则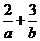 的最小值为( ).
的最小值为( ).
A.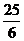 B.
B. C.
C. 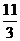 D.
4
D.
4
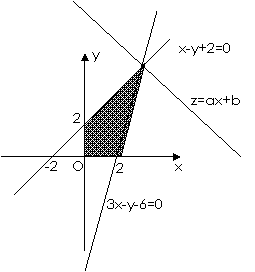
[解析]:不等式表示的平面区域如图所示阴影部分,当直线ax+by= z(a>0,b>0)
过直线x-y+2=0与直线3x-y-6=0的交点(4,6)时,
目标函数z=ax+by(a>0,b>0)取得最大12,
即4a+6b=12,即2a+3b=6, 而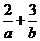 =
=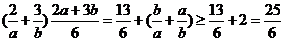 ,故选A.
,故选A.
答案:A
[命题立意]:本题综合地考查了线性规划问题和由基本不等式求函数的最值问题.要求能准确地画出不等式表示的平面区域,并且能够求得目标函数的最值,对于形如已知2a+3b=6,求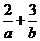 的最小值常用乘积进而用基本不等式解答.
的最小值常用乘积进而用基本不等式解答. 

6.(2009安徽卷理)下列选项中,p是q的必要不充分条件的是
(A)p: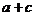 >b+d
, q:
>b+d
, q: >b且c>d
>b且c>d
(B)p:a>1,b>1 q: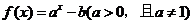 的图像不过第二象限
的图像不过第二象限
(C)p: x=1,
q:
(D)p:a>1,
q:  在
在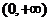 上为增函数
上为增函数
[解析]:由 >b且c>d
>b且c>d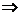
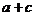 >b+d,而由
>b+d,而由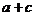 >b+d
>b+d  >b且c>d,可举反例。选A
>b且c>d,可举反例。选A
1.(2009安徽卷理)若不等式组 所表示的平面区域被直线
所表示的平面区域被直线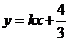 分为面积相等的两部分,则
分为面积相等的两部分,则 的值是
的值是
 (A)
(A)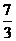 (B)
(B) 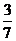 (C)
(C)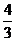 (D)
(D) 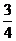
 [解析]:不等式表示的平面区域如图所示阴影部分△ABC
[解析]:不等式表示的平面区域如图所示阴影部分△ABC
由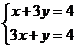 得A(1,1),又B(0,4),C(0,
得A(1,1),又B(0,4),C(0,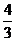 )
)
∴ △ABC=
△ABC=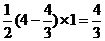 ,设
,设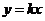 与
与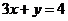 的
的
交点为D,则由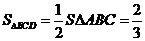 知
知 ,∴
,∴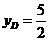
∴ 选A。
选A。
2(2009安徽卷文)不等式组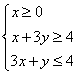 所表示的平面区域的面积等于
所表示的平面区域的面积等于
A. 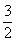 B.
B. 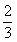
C. 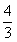 D.
D. 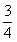
[解析]由 可得
可得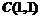 ,故
,故 阴 =
阴 = ,选C。
,选C。
[答案]C
3(2009安徽卷文)“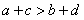 ”是“
”是“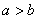 且
且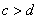 ”的
”的
A. 必要不充分条件 B. 充分不必要条件
C. 充分必要条件 D. 既不充分也不必要条件
[解析]易得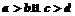 时必有
时必有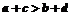 .若
.若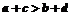 时,则可能有
时,则可能有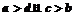 ,选A。
,选A。
[答案]A
4(2009四川卷文)已知 ,
,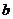 ,
,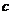 ,
,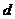 为实数,且
为实数,且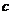 >
>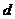 .则“
.则“ >
>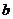 ”是“
”是“ -
-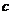 >
>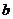 -
-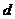 ”的
”的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充要条件 D. 既不充分也不必要条件
[答案]B 

[解析]显然,充分性不成立.又,若 -
-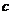 >
>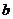 -
-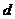 和
和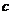 >
>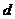 都成立,则同向不等式相加得
都成立,则同向不等式相加得 >
>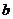
即由“ -
-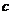 >
>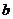 -
-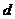 ”
”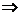 “
“ >
>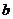 ”
”
5(2009四川卷文)某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨,销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元。该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨.那么该企业可获得最大利润是
A. 12万元 B. 20万元 C. 25万元 D. 27万元
[答案]D
 [解析]设生产甲产品
[解析]设生产甲产品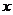 吨,生产乙产品
吨,生产乙产品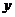 吨,则有关系:
吨,则有关系:
|
|
A原料 |
B原料 |
甲产品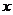 吨 吨 |
3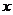 |
2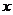 |
乙产品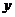 吨 吨 |
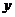 |
3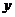 |
则有: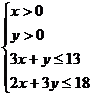
目标函数
作出可行域后求出可行域边界上各端点的坐标,经验证知:
当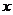 =3,
=3,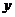 =5时可获得最大利润为27万元,故选D
=5时可获得最大利润为27万元,故选D
43、(03全国卷) (15分)中子星是恒星演化过程的一种可能结果,它的密度很大。现有一中子星,观测到它的自转周期为T=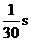 。问该中子星的最小密度应是多少才能维持该星体的稳定,不致因自转而瓦解。计算时星体可视为均匀球体。
。问该中子星的最小密度应是多少才能维持该星体的稳定,不致因自转而瓦解。计算时星体可视为均匀球体。
(引力常数G=6.67×10-11m3/kg·s2)
42、(01上海卷) (10分)(10)1791年,米被定义为:在经过巴黎的子午线上,取从赤道到北极长度的一千万分之一。请由此估算地求的半径R。(答案保留二位有效数字)
(2)太阳与地球的距离为1.5×1011 m,太阳光以平行光束入射到地面。地球表面2/3的面积被水面所覆盖,太阳在一年中辐射到地球表面水面部分的总能量 W约为三1.87×1024J。设水面对太阳辐射的平均反射率为7%,而且将吸收到的35%能量重新辐射出去。太阳辐射可将水面的水蒸发(设在常温、常压下蒸发1kg水需要2.2×106J的能量),而后凝结成雨滴降落到地面。
(a)估算整个地球表面的年平均降雨量(以毫米表示,球面积为4πR2)。
(b)太阳辐射到地球的能量中只有约50%到达地面,W只是其中的一部分。太阳辐射到地球的能量没能全部到达地面,这是为什么?请说明二个理由。
解:(1)2πR×1/4=1.00×107
R=6.37×106 m ①
(2)(a)设太阳在一年中辐射到地球水面部分的总能量为W,W=1.87×1024J
凝结成雨滴年降落到地面水的总质量为m
m=W×0.93×0.65/(2.2×106)=5.14×1017 kg ②
使地球表面覆盖一层水的厚度为h
h=m/ρs地球
h=1.01×103mm ③
整个地球表面年平均降雨量约为1.0×103 mm
(b)大气层的吸收,大气层的散射或反射,云层遮挡等。
评分标准:全题10分。第(1)小题3分,第(2)小题7分。其中(1)得出①给 3分,写出R=6.4×106 m,同样给分。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com