例1．已知大气压强为p₀ cmHg,一端开口的玻璃管内封闭一部分气体，管内水银柱高度为h cm，(或两边水银柱面高度差为h cm)，玻璃管静止，求下列图中封闭理想气体的压强各是多少？

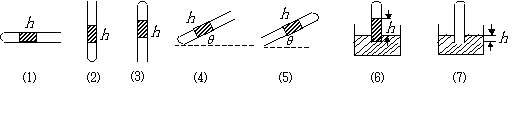解析：将图中的水银柱隔离出来做受力分析；⑺中取与管内气体接触的水银面为研究对象做受力分析． 本题的所有试管的加速度都为零．所以在⑴中：G=N，p₀S=PS；在⑵图中：p₀S+G=pS，p₀S+ρghS=pS，取cmHg(厘米汞柱)为压强单位则有：p= p₀+h；同理，图⑶中试管内气体的压强为：p= p₀-h；采用正交分解法解得：图⑷中：p= p₀+hsinθ；图⑸中：p=p₀-hsinθ；图⑹中取高出槽的汞柱为研究对象，可得到：p= p₀-h；图⑺中取与管内气体接触的水银面(无质量)为研究对象：p₀S+ρghS=pS，p= p₀+h

点评：

(1) 确定封闭气体压强主要是找准封闭气体与水银柱(或其他起隔绝作用的物体)的接触面，利用平衡的条件计算封闭气体的压强．

(2) 封闭气体达到平衡状态时，其内部各处、各个方向上压强值处处相等．

(3) 液体压强产生的原因是重力

(4)液体可将其表面所受压强向各个方向传递．

(1)两容器各侧壁压强的大小关系及压强大小决定于哪些因素？

(2)若两容器同时做自由落体运动，容器侧壁所受压强将怎样变化？

解析：

(1)对于甲容器，上壁压强为零，底面压强最大，侧壁压强自上而下由小变大其大小决定于深度，对于乙容器各处器壁上的压强均相等，其大小决定于气体分子的温度和气体分子的密度。

(2)甲容器做自由落体运动时，处于完全失重状态，器壁各处的压强均为零；乙容器做自由落体运动时，气体分子的温度和气体分子的密度不变，所以器壁各处的压强不发生变化。

点评：要分析、弄清液体压强和气体压强产生的原因是解决本题的关键。

例3．钢瓶内装有高压气体，打开阀门高压气体迅速从瓶口喷出，当内外气压相等时立即关闭阀门。过一段时间后再打开阀门，问会不会再有气体喷出？

解析：第一次打开阀门气体高速喷出，气体迅速膨胀对外做功，但来不及吸热。由热力学第一定律可知，气体内能减少，导致温度突然下降。关闭阀门时，瓶内气体温度低于外界温度，但瓶内压强等于外界气体压强。过一段时间后，通过与外界热交换，瓶内温度升高到和外界温度相同，而瓶的体积没变，故而瓶内气体压强增大。因此，再次打开阀门，会有气体喷出。

点评：此题有两个过程，第一次相当于绝热膨胀过程，第二次是等容升温。

例4．一房间内，上午10时的温度为15⁰C，下午2时的温度为25⁰C，假定大气压无变化，则下午2时与上午10时相比较，房间内的　 (　　)

A．空气密度增大　 　　　　 B．空气分子的平均动增大

C．空气分子速率都增大　　 　　　D．空气质量增大

解析：由于房间与外界相通，外界大气压无变化，因而房间内气体压强不变。但温度升高后，体积膨胀，导致分子数密度减小。所以，房间内空气质量减少，空气分子的平均动增大。但并非每个分子速率都增大，因为单个分子的运动是无规则的。答案B是正确。

点评：本题要求学生正确理解题意，弄清温度变化对分子运动的影响。

例5．如图所示，一气缸竖直放置，气缸内有一质量不可忽略的活塞，将一定量的理想气体封在气缸内，活塞与气缸壁无摩擦，气体处于平衡状态．现保持温度不变把气缸稍微倾斜一点，在达到平衡后，与原来相比，则(　　)

A．气体的压强变大　　　　 B．气体的压强变小

C．气体的体积变大　　　　 D．气体的体积变小

解析：由活塞的受力分析可知,开始封闭气体的压强

P₁=P₀-mg/s,而气缸稍微倾斜一点后，　P₁S　　　　P₂S

由于P₁＜P₂，而温度不变，由气态方程，mg　　θ　mg

则V₂＜V₁，故AD正确．　　　　P₀S　　P₀S

5．理想气体分子间没有相互作用力。注意：一定质量的某种理想气体内能由温度　 决定。

4．一定质量的理想气体的体积、压强、温度之间的关系是： PV/T=常数 　，克拉珀珑方程是：　 PV/T=RM/μ　　 。

2．气体的状态参量有：(p、V、T)

①压强(p)：封闭气体的压强是大量分子对器壁 撞击　 的宏观表现，其决定因素有：1) 温度　　 ；2)　 单位体积内分子数 。

②体积(V)：1m³= 10³ l= 　10⁶ml 。　　

③热力学温度T=　 t+273.15　　 。

1．1atm= 1.01×10⁵　　 　pa= 76　 cmHg，相当于 　10.3　 m高水柱所产生的压强。

3.气体分子运动的特点。气体压强的微观意义。　　　　　　　

2.气体的体积、温度、压强之间的关系.。　　　　　　　　　　

1.气体状态和状态参量。热力学温度。　　　　　　　　　　

例1．雷蒙德·戴维斯因研究来自太阳的电子中微子(v。)而获得了2002年度诺贝尔物理学奖．他探测中微子所用的探测器的主体是一个贮满615t四氯乙烯(C₂Cl₄)溶液的巨桶．电子中微子可以将一个氯核转变为一个氢核，其核反应方程式为 　　　　　　　　　　　　　 ν_e+3717Cl→3718Ar十 0－1e

已知3717Cl核的质量为36.95658 u，3718Ar核的质量为36.95691 u， 0－1e的质量为0.00055 u，1 u质量对应的能量为931.5MeV.根据以上数据，可以判断参与上述反应的电子中微子的最小能量为

(A)0.82 Me V　　 (B)0.31 MeV　　 (C)1.33 MeV　　 (D)0.51 MeV

[解析]由题意可得：电子中微子的能量E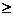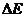=mc²-(m_Ar+m_e-m_Cl)·931.5MeV

=(36.95691+0.00055-36.95658)×931.5MeV

=0.82MeV

则电子中微子的最小能量为　 E_min=0.82MeV

　 [点评] 　应用爱因斯坦质能方程时，注意单位的使用。当用kg单位，c用m/s时，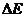

单位是J，也可像本题利用1 u质量对应的能量为931.5MeV.

例2、质子、中子和氘核的质量分别为m₁、m₂、m₃，质子和中子结合成氘核时，发出γ射线，已知普朗克恒量为h，真空中光速为c，则γ射线的频率υ＝ ______　 ．

[解析]　 核反应中释放的能量ΔE＝Δmc²以释放光子的形式释放出来，由于光子的能量为hυ，依能量守恒定律可知：hυ=Δmc²据此便可求出光子的频率。

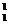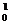　质子和中子结合成氘核：H+n　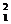 H+γ这个核反应的质量亏损为：

　　　Δm＝m₁+m₂－m₃

根据爱因斯坦质能方程　 ΔE＝Δmc²

　 此核反应放出的能量　 ΔE＝(m₁+m₂－m)c²

　　 以γ射线形式放出，由E＝hυ

　　　　　　　 υ=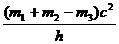

[点评]　 此题考查计算质量亏损，根据爱因斯坦质能方程确定核能．关键是对质量亏损的理解和确定．

例3. 核聚变能是一种具有经济性能优越、安全可靠、无环境污染等优势的新能源。近年来，受控核聚变的科学可行性已得到验证，目前正在突破关键技术，最终将建成商用核聚变电站。一种常见的核聚变反应是由氢的同位素氘(又叫重氢)和氚(又叫超重氢)聚合成氦，并释放一个中子了。若已知氘原子的质量为2.0141u，氚原子的质量为3.0160u，氦原子的质量为4.0026u，中子的质量为1.0087u，1u=1.66×10^-27kg。

⑴写出氘和氚聚合的反应方程。

⑵试计算这个核反应释放出来的能量。

⑶若建一座功率为3.0×10⁵kW的核聚变电站，假设聚变所产生的能量有一半变成了电能，每年要消耗多少氘的质量？

(一年按3.2×10⁷s计算，光速c=3.00×10⁸m/s，结果取二位有效数字)

[解析](1)(3)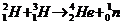

　　　 (2)ΔE=Δmc²=(2．0141+3．0160-4．0026-1．0087)×1．66×10^-27×3²×10¹⁶J=2.8×10^-12J

(3)M=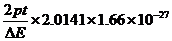

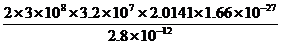==23kg

例 4．众所周知，地球围绕着太阳做椭圆运动，阳光普照大地，万物生长．根据学过的知识试论述说明随着岁月的流逝，地球公转的周期，日、地的平均距离及地球表面的温度的变化趋势．

[解析]　 太阳内部进行着剧烈的热核反应，在反应过程中向外释放着巨大的能量，这些能量以光子形式放出．根据爱因斯坦质能关系： ΔE＝Δm·c²　 ， 知太阳质量在不断减小．

地球绕太阳旋转是靠太阳对地球的万有引力来提供向心力　 G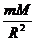=mω²R， 现因M减小，即提供的向心力减小，不能满足所需的向心力，地球将慢慢向外做离心运动，使轨道半径变大，日地平均距离变大．

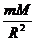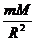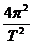由上式可知，左边的引力G减小，半径R增大，引起地球公转的角速度变化，从而使公转周期变化 G=mR，T²=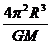，即 T增大．

　　 一方面，因太阳质量变小，发光功率变小；另一方面，日地距离变大，引起辐射到地球表面的能量减小，导致地球表面温度变低．

　 [点评]　 该题集原子物理与力学为一体，立意新颖，将这一周而复始的自然用所学知识一步一步说明，是一道考查能力、体现素质的好题．　

5．链式反应

　 　一个重核吸收一个中子后发生裂变时，分裂成两个中等质量核，同时释放若干个中子，如果这些中子再引起其它重核的裂变，就可以使这种裂变反应不断的进行下去，这种反应叫重核裂变的链式反应