2、求解策略

变换物理模型，是将陌生的物理模型与熟悉的物理模型相比较，分析异同并从中挖掘其内在联系，从而建立起熟悉模型与未知现象之间相互关系的一种特殊解题方法.巧妙地运用“类同”变换，“类似”变换，“类异”变换，可使复杂、陌生、抽象的问题变成简单、熟悉、具体的题型，从而使问题大为简化.

解决电磁感应电路问题的关键就是借鉴或利用相似原型来启发理解和变换物理模型，即把电磁感应的问题等效转换成稳恒直流电路，把产生感应电动势的那部分导体等效为内电路.感应电动势的大小相当于电源电动势.其余部分相当于外电路，并画出等效电路图.此时，处理问题的方法与闭合电路求解基本一致，惟一要注意的是电磁感应现象中，有时导体两端有电压，但没有电流流过，这类似电源两端有电势差但没有接入电路时，电流为零.

[例3]据报道，1992年7月，美国“阿特兰蒂斯”号航天飞机进行了一项卫星悬绳发电实验，实验取得了部分成功.航天飞机在地球赤道上空离地面约3000 km处由东向西飞行，相对地面速度大约6.5×10³ m/s，从航天飞机上向地心方向发射一颗卫星，携带一根长20 km，电阻为800 Ω的金属悬绳，使这根悬绳与地磁场垂直，做切割磁感线运动.假定这一范围内的地磁场是均匀的.磁感应强度为4×10^-5T，且认为悬绳上各点的切割速度和航天飞机的速度相同.根据理论设计，通过电离层(由等离子体组成)的作用，悬绳可以产生约3 A的感应电流，试求：

(1)金属悬绳中产生的感应电动势；

(2)悬绳两端的电压；

(3)航天飞机绕地球运行一圈悬绳输出的电能(已知地球半径为6400 km).

命题意图：考查考生信息摄取、提炼、加工能力及构建物理模型的抽象概括能力.

错解分析：考生缺乏知识迁移运用能力和抽象概括能力，不能于现实情景中构建模型(切割磁感线的导体棒模型)并进行模型转换(转换为电源模型及直流电路模型)，无法顺利运用直流电路相关知识突破.

解题方法与技巧：将飞机下金属悬绳切割磁感线产生感应电动势看作电源模型，当它通过电离层放电可看作直流电路模型.如图所示.

(1)金属绳产生的电动势：

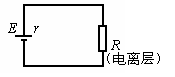E=Blv=4×10^-5×20×10³×6.5×10³ V=5.2×10³ V

(2)悬绳两端电压，即路端电压可由闭合电路欧姆定律得：

U=E-Ir=5.2×10³-3×800 V=2.8×10³ V

(3)飞机绕地运行一周所需时间

t=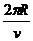=s=9.1×10³ s

则飞机绕地运行一圈输出电能：

E=UIt=2800×3×9.1×10³ J=7.6×10⁷ J

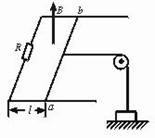
[例4]如图所示，竖直向上的匀强磁场，磁感应强度B=0.5 T，并且以=0.1 T/s在变化，水平轨道电阻不计，且不计摩擦阻力，宽0.5 m的导轨上放一电阻R₀=0.1 Ω的导体棒，并用水平线通过定滑轮吊着质量M=0.2 kg的重物，轨道左端连接的电阻R=0.4 Ω，图中的l=0.8 m，求至少经过多长时间才能吊起重物.

命题意图：考查理解能力、推理能力及分析综合能力

错解分析：(1)不善于逆向思维，采取执果索因的有效途径探寻解题思路；(2)实际运算过程忽视了B的变化，将B代入F_安=BIl_ab，导致错解.

解题方法与技巧：

由法拉第电磁感应定律可求出回路感应电动势：E=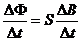　　　　　　　 ①

由闭合电路欧姆定律可求出回路中电流　　 I=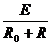　　　　　　　 　　　　　　　 ②

由于安培力方向向左，应用左手定则可判断出电流方向为顺时针方向(由上往下看).再根据楞次定律可知磁场增加，在t时磁感应强度为：　 B′ =(B+·t)　　　　　　　　 ③

此时安培力为　　　 F_安=B′Il_ab　　　　　 　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ④

由受力分析可知　 F_安=mg　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ⑤

由①②③④⑤式并代入数据：t=495 s

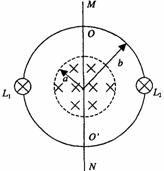[例5](2001年上海卷)半径为a的圆形区域内有均匀磁场，磁感强度为B=0.2T，磁场方向垂直纸面向里，半径为b的金属圆环与磁场同心地放置，磁场与环面垂直，其中a=0.4m，b=0.6m，金属环上分别接有灯L₁、L₂，两灯的电阻均为R =2Ω，一金属棒MN与金属环接触良好，棒与环的电阻均忽略不计

(1)若棒以v₀=5m/s的速率在环上向右匀速滑动，求棒滑过圆环直径OO′ 的瞬时(如图所示)MN中的电动势和流过灯L₁的电流。

(2)撤去中间的金属棒MN，将右面的半圆环OL₂O′ 以OO′ 为轴向上翻转90º，若此时磁场随时间均匀变化，其变化率为ΔB/Δt=4T/s，求L₁的功率。

解析：(1)棒滑过圆环直径OO′ 的瞬时，MN中的电动势

E₁=B2a v=0.2×0.8×5=0.8V　　　　　 ①

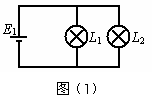
等效电路如图(1)所示，流过灯L₁的电流

I₁=E₁/R=0.8/2=0.4A　　　　　　 ②

(2)撤去中间的金属棒MN，将右面的半圆环OL₂O′ 以OO′ 为轴向上翻转90º，半圆环OL₁O′中产生感应电动势，相当于电源，灯L₂为外电路，等效电路如图(2)所示，感应电动势

E₂=ΔФ/Δt=0.5×πa²×ΔB/Δt=0.32V　　 ③

L₁的功率

P₁=(E­₂/2)²/R=1.28×10²W

电磁感应电路的分析与计算以其覆盖知识点多，综合性强，思维含量高，充分体现考生能力和素质等特点，成为历届高考命题的特点.

1、命题特点

对电磁感应电路的考查命题，常以学科内综合题目呈现，涉及电磁感应定律、直流电路、功、动能定理、能量转化与守恒等多个知识点，突出考查考生理解能力、分析综合能力，尤其从实际问题中抽象概括构建物理模型的创新能力.

3、画图象时要注意横、纵坐标的单位长度定义或表达

[例1]如图所示，平行导轨置于磁感应强度为B的匀强磁场中(方向向里)，间距为L，左端电阻为R，其余电阻不计，导轨右端接一电容为C的电容器。现有一长2L的金属棒ab放在导轨上，ab以a为轴顺时针转过90°的过程中，通过R的电量为多少？

解析：(1)由ab棒以a为轴旋转到b端脱离导轨的过程中，产生的感应电动势一直增大，对C不断充电，同时又与R构成闭合回路。ab产生感应电动势的平均值

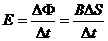　　 ①

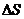表示ab扫过的三角形的面积，即　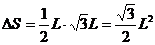　　 ②

通过R的电量　　　 ③

由以上三式解得　　　 ④

在这一过程中电容器充电的总电量Q=CU_m　　 ⑤

U_m为ab棒在转动过程中产生的感应电动势的最大值。即

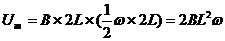　　 ⑥

联立⑤⑥得：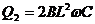

(2)当ab棒脱离导轨后(对R放电，通过R的电量为 Q₂，所以整个过程中通过 R的总电量为：

　 Q=Q₁+Q₂=

电磁感应中“双杆问题”分类解析

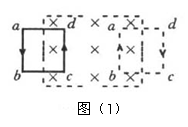
[例2]匀强磁场磁感应强度 B=0.2 T，磁场宽度L=3rn，一正方形金属框边长ab=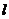=1m，每边电阻r=0.2Ω，金属框以v=10m/s的速度匀速穿过磁场区，其平面始终保持与磁感线方向垂直，如图所示，求：

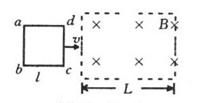
(1)画出金属框穿过磁场区的过程中，金属框内感应电流的I-t图线

(2)画出ab两端电压的U-t图线

解析：线框进人磁场区时

E₁=B l v=2 V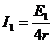，=2.5 A

方向沿逆时针，如图(1)实线abcd所示，感电流持续的时间t₁=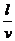=0.1 s

线框在磁场中运动时：E₂=0，I₂=0

无电流的持续时间：t₂=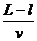=0.2 s，

线框穿出磁场区时：E₃= B l v=2 V，=2.5 A

此电流的方向为顺时针，如图(1)虚线abcd所示，规定电流方向逆时针为正，得I-t图线如图(2)所示

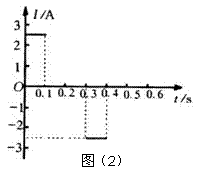(2)线框进人磁场区ab两端电压

U₁=I₁ r=2.5×0.2=0.5V

线框在磁场中运动时；b两端电压等于感应电动势

U₂=B l v=2V

线框出磁场时ab两端电压：U₃=E - I₂ r=1.5V

由此得U-t图线如图(3)所示

点评：将线框的运动过程分为三个阶段，第一阶段ab为外电路，第二阶段ab相当于开路时的电源，第三阶段ab是接上外电路的电源

2、在图象中E、I、B等物理量的方向是通过正负值来反映

1、定性或定量地表示出所研究问题的函数关系

3、利用电路规律求解，主要有欧姆定律，串并联规律等

2、分析电路结构，画等效电路图

1、确定电源：首先判断产生电磁感应现象的那一部分导体(电源)，其次利用或求感应电动势的大小，利用右手定则或楞次定律判断电流方向。

(二)电磁感应中的一个重要推论--安培力的冲量公式

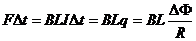
感应电流通过直导线时，直导线在磁场中要受到安培力的作用，当导线与磁场垂直时，安培力的大小为F=BLI。在时间△t内安培力的冲量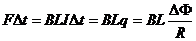，式中q是通过导体截面的电量。利用该公式解答问题十分简便，下面举例说明这一点。

[例7]如图所示，在光滑的水平面上，有一垂直向下的匀强磁场分布在宽为L的区域内，有一个边长为a(a<L)的正方形闭合线圈以初速v₀垂直磁场边界滑过磁场后速度变为v(v<v₀)那么

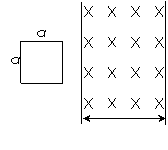A．完全进入磁场中时线圈的速度大于(v₀+v)/2；

B．安全进入磁场中时线圈的速度等于(v₀+v)/2；

C．完全进入磁场中时线圈的速度小于(v₀+v)/2；

D．以上情况A、B均有可能，而C是不可能的

解析：设线圈完全进入磁场中时的速度为v_x。线圈在穿过磁场的过程中所受合外力为安培力。对于线圈进入磁场的过程，据动量定理可得：

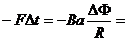
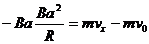
对于线圈穿出磁场的过程，据动量定理可得：

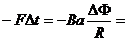
由上述二式可得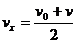，即B选项正确。

[例8]光滑U型金属框架宽为L，足够长，其上放一质量为m的金属棒ab，左端连接有一电容为C的电容器，现给棒一个初速v₀，使棒始终垂直框架并沿框架运动，如图所示。求导体棒的最终速度。

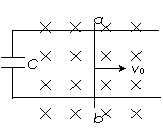解析：当金属棒ab做切割磁力线运动时，要产生感应电动势，这样，电容器C将被充电，ab棒中有充电电流存在，ab棒受到安培力的作用而减速，当ab棒以稳定速度v匀速运动时，有：

BLv=U_C=q/C

而对导体棒ab利用动量定理可得：

-BLq=mv-mv₀

由上述二式可求得：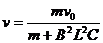

(一)电磁感应中的“双杆问题”

电磁感应中“双杆问题”是学科内部综合的问题，涉及到电磁感应、安培力、牛顿运动定律和动量定理、动量守恒定律及能量守恒定律等。要求学生综合上述知识，认识题目所给的物理情景，找出物理量之间的关系，因此是较难的一类问题，也是近几年高考考察的热点。

考题回顾

[例3]如图所示，两根平行的金属导轨，固定在同一水平面上，磁感应强度B=0.50T的匀强磁场与导轨所在平面垂直，导轨的电阻很小，可忽略不计。导轨间的距离l=0.20m。两根质量均为m=0.10kg的平行金属杆甲、乙可在导轨上无摩擦地滑动，滑动过程中与导轨保持垂直，每根金属杆的电阻为R=0.50Ω。在t=0时刻，两杆都处于静止状态。现有一与导轨平行、大小为0.20N的恒力F作用于金属杆甲上，使金属杆在导轨上滑动。经过t=5.0s，金属杆甲的加速度为a=1.37m/s²，问此时两金属杆的速度各为多少？

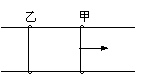解析：设任一时刻t两金属杆甲、乙之间的距离为x，速度分别为v₁和v₂，经过很短的时间△t，杆甲移动距离v₁△t，杆乙移动距离v₂△t，回路面积改变

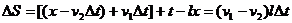
由法拉第电磁感应定律，回路中的感应电动势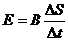

回路中的电流

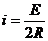
杆甲的运动方程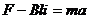

由于作用于杆甲和杆乙的安培力总是大小相等，方向相反，所以两杆的动量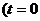时为0)等于外力F的冲量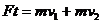

联立以上各式解得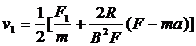　

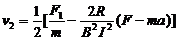
代入数据得

点评：题中感应电动势的计算也可以直接利用导体切割磁感线时产生的感应电动势公式和右手定则求解：设甲、乙速度分别为v₁和v₂，两杆切割磁感线产生的感应电动势分别为

E₁＝Blv₁ ，E₂＝Blv₂

由右手定则知两电动势方向相反，故总电动势为E＝E₂―E₁＝Bl(v₂－v₁)。

分析甲、乙两杆的运动，还可以求出甲、乙两杆的最大速度差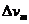：开始时，金属杆甲在恒力F作用下做加速运动，回路中产生感应电流，金属杆乙在安培力作用下也将做加速运动，但此时甲的加速度肯定大于乙的加速度，因此甲、乙的速度差将增大。根据法拉第电磁感应定律，感应电流将增大，同时甲、乙两杆所受安培力增大，导致乙的加速度增大，甲的加速度减小。但只要a_甲>a_乙，甲、乙的速度差就会继续增大，所以当甲、乙两杆的加速度相等时，速度差最大。此后，甲、乙两杆做加速度相等的匀加速直线运动。

设金属杆甲、乙的共同加速度为a，回路中感应电流最大值I_m.对系统和乙杆分别应用牛顿第二定律有：F=2ma；BLI_m=ma.

由闭合电路敬欧姆定律有E=2I_mR，而

由以上各式可解得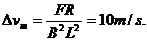

[例4]图中a₁b₁c₁d₁和a₂b₂c₂d₂为在同一竖直平面内的金属导轨，处在磁感应强度为B的匀强磁场中，磁场方向垂直于导轨所在平面(纸面)向里。导轨的a₁b₁段与a₂b₂段是竖直的，距离为l₁；c₁d₁段与c₂d₂段也是竖直的，距离为l₂。x₁ y₁与x₂ y₂为两根用不可伸长的绝缘轻线相连的金属细杆，质量分别为和m₁和m₂，它们都垂直于导轨并与导轨保持光滑接触。两杆与导轨构成的回路的总电阻为R。F为作用于金属杆x₁y₁上的竖直向上的恒力。已知两杆运动到图示位置时，已匀速向上运动，求此时作用于两杆的重力的功率的大小和回路电阻上的热功率。

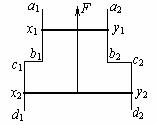
解析：设杆向上的速度为v，因杆的运动，两杆与导轨构成的回路的面积减少，从而磁通量也减少。由法拉第电磁感应定律，回路中的感应电动势的大小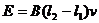　　　 ①

回路中的电流　　 　　　　　　　　②

电流沿顺时针方向。两金属杆都要受到安培力作用，作用于杆x₁y₁的安培力为

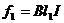　　　　　　 ③

方向向上，作用于杆x₂y₂的安培力为　　　　 　　　　　　④

方向向下，当杆作匀速运动时，根据牛顿第二定律有　 ⑤

解以上各式得　　　 　　　　　　　　　⑥

　　　　 　　　⑦

作用于两杆的重力的功率的大小　　 　　　　　　⑧

电阻上的热功率　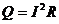　　 　　　　　　　　　　　　　　⑨

由⑥⑦⑧⑨式，可得

　　　 ⑩

　　　　　　　 ⑾

下面对“双杆”类问题进行分类例析

1、“双杆”向相反方向做匀速运动

当两杆分别向相反方向运动时，相当于两个电池正向串联。

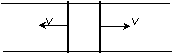[例5]两根相距d=0.20m的平行金属长导轨固定在同一水平面内，并处于竖直方向的匀强磁场中，磁场的磁感应强度B=0.2T，导轨上面横放着两条金属细杆，构成矩形回路，每条金属细杆的电阻为r=0.25Ω，回路中其余部分的电阻可不计.已知两金属细杆在平行于导轨的拉力的作用下沿导轨朝相反方向匀速平移，速度大小都是v=5.0m/s，如图所示.不计导轨上的摩擦.

(1)求作用于每条金属细杆的拉力的大小.

(2)求两金属细杆在间距增加0.40m的滑动过程中共产生的热量.

解析：(1)当两金属杆都以速度v匀速滑动时，每条金属杆中产生的感应电动势分别为： E₁=E₂=Bdv

由闭合电路的欧姆定律，回路中的电流强度大小为：

因拉力与安培力平衡，作用于每根金属杆的拉力的大小为F₁=F₂=IBd。

由以上各式并代入数据得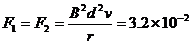N

(2)设两金属杆之间增加的距离为△L，则两金属杆共产生的热量为，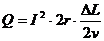

代入数据得　　 Q=1.28×10^-2J.

2.“双杆”同向运动，但一杆加速另一杆减速

当两杆分别沿相同方向运动时，相当于两个电池反向串联。

[例6]两根足够长的固定的平行金属导轨位于同一水平面内，两导轨间的距离为L。导轨上面横放着两根导体棒ab和cd，构成矩形回路，如图所示．两根导体棒的质量皆为m，电阻皆为R，回路中其余部分的电阻可不计．在整个导轨平面内都有竖直向上的匀强磁场，磁感应强度为B．设两导体棒均可沿导轨无摩擦地滑行．开始时，棒cd静止，棒ab有指向棒cd的初速度v₀．若两导体棒在运动中始终不接触，求：

(1)在运动中产生的焦耳热最多是多少．

(2)当ab棒的速度变为初速度的3/4时，cd棒的加速度是多少？

解析：ab棒向cd棒运动时，两棒和导轨构成的回路面积变小，磁通量发生变化，于是产生感应电流．ab棒受到与运动方向相反的安培力作用作减速运动，cd棒则在安培力作用下作加速运动．在ab棒的速度大于cd棒的速度时，回路总有感应电流，ab棒继续减速，cd棒继续加速．两棒速度达到相同后，回路面积保持不变，磁通量不变化，不产生感应电流，两棒以相同的速度v作匀速运动．

(1)从初始至两棒达到速度相同的过程中，两棒总动量守恒，有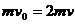　　　　　　　 根据能量守恒，整个过程中产生的总热量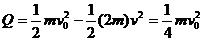　

(2)设ab棒的速度变为初速度的3/4时，cd棒的速度为v₁，则由动量守恒可知：

此时回路中的感应电动势和感应电流分别为：，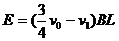

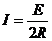
此时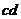棒所受的安培力： 　　　 ，所以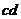棒的加速度为 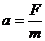　　　　　　　　　　　　　 由以上各式，可得　　　 。

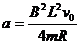3. “双杆”中两杆都做同方向上的加速运动。

“双杆”中的一杆在外力作用下做加速运动，另一杆在安培力作用下做加速运动，最终两杆以同样加速度做匀加速直线运动。如[例3](2003年全国理综卷)

4．“双杆”在不等宽导轨上同向运动。

“双杆”在不等宽导轨上同向运动时，两杆所受的安培力不等大反向，所以不能利用动量守恒定律解题。如