
2、BD;
3.(徐州市2008届摸底考试)据报道,我国将于07年秋季发射“嫦娥1号”卫星,某同学查阅了一些与地球、月球有关的数据资料如下:
地球半径R=6400km,月球半径r=1740km,地球表面重力加速度g0=9.80m/s2,月球表面重力加速度g′=1.56m/s2,月球绕地球转动一周时间为T=27.3天
请你利用上述物理量的符号表示:
(1)“嫦娥1号”卫星绕月球表面运动一周所需的时间;
(2)月球表面到地球表面之间的最近距离。
答案:1、(1)如图
(2)0.05m/s2 (3)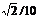 m/s;
m/s;
2.(07全国卷Ⅱ)假定地球、月亮都是静止不动,用火箭从地球沿地月连线向月球发射一探测器。假定探测器在地球表面附近脱离火箭。用W表示探测器从脱离火箭处飞到月球过程中克服地球引力做的功,用Ek表示探测器脱离火箭时的动能,若不计空气阻力,则( )
A.Ek必须大于或等于W,探测器才能到达月球
B.Ek小于W,探测器也可能到达月球
C.Ek=W/2,探测器一定能到达月球
D.Ek=W/2,探测器一定不能到达月球
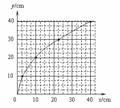
1.(东台市2008届第一次调研)如图甲所示,在一端封闭、长约lm的玻璃管内注满清水,水中放一个蜡烛做的蜡块,将玻璃管的开口端用胶塞塞紧.然后将这个玻璃管倒置,在蜡块沿玻璃管上升的同时,将玻璃管水平向右移动.假设从某时刻开始计时,蜡块在玻璃管内每1s上升的距离都是10cm,玻璃管向右匀加速平移,每1s通过的水平位移依次是2.5cm、7.5cm、12.5cm、17.5cm.图乙中,y表示蜡块竖直方向的位移,x表示蜡块随玻璃管通过的水平位移,t=0时蜡块位于坐标原点。
(1)请在图乙中画出蜡块4s内的轨迹;
(2)求出玻璃管向右平移的加速度;
(3)求t=2s时蜡块的速度v。
4.推论法:记住一些重要结论,如一些圆周运动的临界值,再如常用到的黄金代换“GM=gR2”等等。一些很重要的表达式及数据对于迅速分析题目很有帮助。


类型一利用运动的合成与分解解题
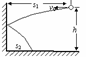 [例1]在离地面高为h,离竖直光滑墙的水平距离为s1处,有一小球以v0的速度向墙水平抛出,如图所示。小球与墙碰撞后落地,不计碰撞过程中的能量损失,也不考虑碰撞的时间,则落地点到墙的距离s2为多少?
[例1]在离地面高为h,离竖直光滑墙的水平距离为s1处,有一小球以v0的速度向墙水平抛出,如图所示。小球与墙碰撞后落地,不计碰撞过程中的能量损失,也不考虑碰撞的时间,则落地点到墙的距离s2为多少?
导示: 小球抛出后先做平抛后作斜抛,题目要求的是斜抛的水平距离。
该题有两种处理方法:方法一,分段处理,先分解平抛,后再分解斜抛,从而求得问题的结果。 方法二,对整个过程进行研究,抓住运动过程中的受力特点,可以将该曲线运动向水平和竖直分解,竖直方向只受重力,做自由落体运动;水平方向不受外力,所以先水平向左做匀速,碰后向右做速度相同的匀速直线运动。
竖直方向:由h=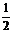 gt2得t=
gt2得t=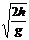
 水平方向:s1+s2=v0t得s2=v0
水平方向:s1+s2=v0t得s2=v0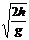 -s1
-s1
故答案为:v0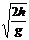 -s1
-s1

 处理曲线运动时,其基本思路是将曲线运动分解为两个直线运动去讨论,这种方法不仅对抛体运动适用,对其他较为复杂曲线运动也适用,而且有时候显得更为方便。这一点,在处理带电粒子在电场中运动的问题时也会有所体现。
处理曲线运动时,其基本思路是将曲线运动分解为两个直线运动去讨论,这种方法不仅对抛体运动适用,对其他较为复杂曲线运动也适用,而且有时候显得更为方便。这一点,在处理带电粒子在电场中运动的问题时也会有所体现。
类型二“黄金代换”的应用
在卫星问题中,一般并不告诉我们地球的质量M,而是告诉重力加速度,由于地球表面重力加速度与物体所受重力近似相等,所以可得:mg=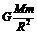 即GM=gR2。我们把GM=gR2称为“黄金代换”。
即GM=gR2。我们把GM=gR2称为“黄金代换”。
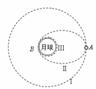 [例2](启东市2008届高三第一次调研)我国在2010年实现探月计划--“嫦娥工程”。同学们也对月球有了更多的关注。
[例2](启东市2008届高三第一次调研)我国在2010年实现探月计划--“嫦娥工程”。同学们也对月球有了更多的关注。
(1)若已知地球半径为R,地球表面的重力加速度为g,月球绕地球运动的周期为T,月球绕地球的运动近似看做匀速圆周运动,试求出月球绕地球运动的轨道半径;
(2)若宇航员随登月飞船登陆月球后,在月球表面某处以速度v0竖直向上抛出一个小球,经过时间t,小球落回抛出点.已知月球半径为r,万有引力常量为G,试求出月球的质量M月.
导示: (1)对于地月系统,月球绕着地球做圆周运动,根据万有引力定律提供向心力有:
G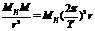
又 mg = G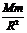
解得:r =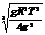
(2)设月球表面处的重力加速度为g月,根据在月球表面作竖直上抛的物体可求得g月
即: V0=g月t/2
又g月 = GM月/r2
解得:M月 =2v0r2/Gt

 在研究卫星的问题中,若已知中心天体表面的重力加速度g0时,常运用GM=g0R2作为桥梁,可以把“地上"和 “天上”联系起来。这一代换在卫星问题中相当普遍,所以应熟练掌握。但应注意,代换式中R是地球半径,而不是卫星运行半径,这一点要在列式中注意,一定要采用不同符号,不可混淆。
在研究卫星的问题中,若已知中心天体表面的重力加速度g0时,常运用GM=g0R2作为桥梁,可以把“地上"和 “天上”联系起来。这一代换在卫星问题中相当普遍,所以应熟练掌握。但应注意,代换式中R是地球半径,而不是卫星运行半径,这一点要在列式中注意,一定要采用不同符号,不可混淆。
类型三卫星的变轨问题
卫星绕天体在圆轨道上的匀速圆周运动是稳定的运行,此时万有引力提供向心力.在不同的轨道,卫星稳定运行的速度不同。当卫星由于某种原因速度突然改变时(开启或关闭发动机或空气阻力作用),万有引力就不再等于向心力,卫星将做变轨运行。
[例3] (南通市2008届基础调研)“神州六号”飞船的成功飞行为我国在2010年实现探月计划--“嫦娥工程”获得了宝贵的经验.假设月球半径为R,月球表面的重力加速度为g0,飞船在距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B再次点火进入月球近月轨道Ⅲ绕月球作圆周运动.求:
(1)飞船在轨道Ⅰ上的运行速率;
(2)飞船在A点处点火时,动能如何变化;
(3)飞船在轨道Ⅲ绕月球运行一周所需的时间.
导示: (1)设月球的质量为M,飞船的质量为m,则
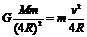
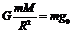
解得 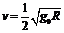
(2)飞船在A点处点火,由轨道Ⅰ变轨进入椭圆轨道Ⅱ,在做近心运动,所以是在减速运动,故动能减小;
(3)设飞船在轨道Ⅲ绕月球运行一周所需的时间为T,则:
解得:

 当卫星的速度突然增加时,F<mv2/r,即万有引力不足以提供向心力,卫星将做离心运动,脱离原来的圆轨道,轨道半径变大,但卫星一旦进入新的轨道运行,由v=
当卫星的速度突然增加时,F<mv2/r,即万有引力不足以提供向心力,卫星将做离心运动,脱离原来的圆轨道,轨道半径变大,但卫星一旦进入新的轨道运行,由v=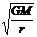 知其运行速度要减小;当卫星的速度突然减小时,F> mv2/r,即万有引力大于卫星所需的向心力,因此卫星将做向心运动,同样会脱离原来的圆轨道,轨道半径变小,进入新轨道运行速度将增大。卫星的发射和回收就是利用了这一原理。
知其运行速度要减小;当卫星的速度突然减小时,F> mv2/r,即万有引力大于卫星所需的向心力,因此卫星将做向心运动,同样会脱离原来的圆轨道,轨道半径变小,进入新轨道运行速度将增大。卫星的发射和回收就是利用了这一原理。


3.对比法:对比研究平抛运动和类平抛运动;匀速圆周运动和非匀速圆周运动,随地面一起的圆周运动和脱离地面的卫星运动,极地卫星和赤道卫星;第一宇宙速度,第二宇宙速度和第三宇宙速度所界定的情境区别等等。
2.极限分析法:常用此法分析圆周运动或平抛运动的临界状态。
1.等效法:有恒定的电场力参与的圆周运动,可以把重力与电场力的合力等效为新的重力mg′,新重力的方向即为合力的方向,据此确定圆周运动的等效最高点和最低点,类平抛运动的处理方法也属于等效法。
4.天体问题的处理方法:
(1)建立一种模型
在分析天体问题时,首先应把研究对象看作质点.这样,天体的运动就抽象为一个质点绕另一个质点的匀速圆周运动模型.
(2)抓住两条思路
①利用在中心天体表面或附近,万有引力近似等于重力,
G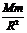 =mg0(g0表示天体表面的重力加速度)。
=mg0(g0表示天体表面的重力加速度)。
②利用万有引力提供向心力。
由此得到一个基本方程G =ma加
=ma加

3.竖直面内的圆周运动
物体在竖直面内做圆周运动时,绝大多数属于变速圆周运动.在不同的约束条件下,物体能完成圆周运动的条件也是不同的.在绳(或沿圆环内侧运动)约束下,物体在最高点的速度v≥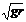 ,在杆(管或弧形轨道外侧等)约束下,物体在最高点的速度v≥0.审题时一定要分清是绳模型还是杆模型,这是前提。
,在杆(管或弧形轨道外侧等)约束下,物体在最高点的速度v≥0.审题时一定要分清是绳模型还是杆模型,这是前提。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com