11．若一个m，n均为非负整数的有序数对(m，n)，在做m+n的加法时各位均不会进位，则称(m，n)为“简单的”有序数对，m+n称为有序数对(m，n)的值，那么值为1942的“简单的”有序数对的个数是________．

答案：300

解析：由题意可知m+n＝1942，当m、n中一个数确定时，另一个数也就唯一确定了，所以不妨设m＝1000x₁+100x₂+10x₃+x₄，则x₁有2种不同取法，x₂有10种不同取法，x₃有5种不同取法，x₄有3种不同取法，所以所求的有序数对的个数为2×10×5×3＝300.

10．在2008年奥运选手选拔赛上，8名男运动员参加100米决赛．其中甲、乙、丙三人必须在1、2、3、4、5、6、7、8八条跑道的奇数号跑道上，则安排这8名运动员比赛的方式共有________种．

答案：2880

解析：分两步安排这8名运动员．

第一步：安排甲、乙、丙三人，共有1、3、5、7四条跑道可安排，所以安排方式有4×3×2＝24种．

第二步：安排另外5人，可在2、4、6、8及余下的一条奇数号跑道安排，所以安排方式有5×4×3×2×1＝120种．

∴安排这8人的方式有24×120＝2880种．

9．从班委会5名成员中选出3名，分别担任班级学习委员、文娱委员与体育委员，其中甲、乙二人不能担任文娱委员，则不同的选法共有__________种．(用数字作答)

答案：36

解析：A·A＝3×4×3＝36.

8．(2008·辽宁)一生产过程有4道工序，每道工序需要安排一人照看，现从甲、乙、丙等6名工人中安排4人分别照看一道工序，第一道工序只能从甲、乙两工人中安排1人，第四道工序只能从甲、丙两工人中安排1人，则不同的安排方案共有(　)

A．24种　 　　　　　　　　　　　　　　　　　　　　　　　　　 B．36种

C．48种 　　　　　　　　　　　　　　　　　　　　　　　　　　 D．72种

答案：B

解析：分两种情况，若甲在第一道工序，则丙必在第四道工序，其余两道工序没有限制，共有A＝4×3＝12种安排方法；若甲不在第一道工序，则第四道工序有两种排法，其余两道工序有A＝12种安排方法，故共有12+2×12＝36种．故选B.

7．(2008·天津)有8张卡片分别标有数字1,2,3,4,5,6,7,8，从中取出6张卡片排成3行2列，要求3行中仅有中间行的两张卡片上的数字之和为5，则不同的排法共有(　)

A．1344种　 　　　　　　　　　　　　　　　　　　　　　　　　 B．1248种

C．1056种　 　　　　　　　　　　　　　　　　　　　　　　　　 D．960种

答案：B

解析：中间行两张卡片为1,4或2,3，且另两行不可同时出现这两组数字．①用间接法，先写出中间行为(1,4)或(2,3)，C·A·A；②去掉两行同时出现1,4或2,3，(AC)²A，所以CAA－(AC)²A＝1440－192＝1248，故选B.

6.

(2008·全国Ⅰ)如右图，一环形花坛分成A、B、C、D四块．现有4种不同的花供选种，要求在每块里种1种花，且相邻的2块种不同的花，则不同的种法总数为(　)

A．96　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B．84

C．60　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．48

答案：B

解法一：当选两种不同花时，有A＝12种，当选三种不同花时有CCA＝48种，当选四种不同花时有A＝24种，

∴共有12+48+24＝84种．故选B.

解法二：当A、C种同一种花时，有CCC＝36种，当A、C种不同的花时，有ACC＝48种，共有36+48＝84种．故选B.

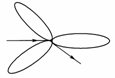
5．一植物园参观路径如图所示，若要全部参观并且路线不重复，则不同的参观路线种数共有(　)

A．6种　 　　　　　　　　　　　　　　　　　　　　　　　　　　 B．8种

C．36种 　　　　　　　　　　　　　　　　　　　　　　　　　　 D．48种

答案：D

解析：

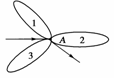
如图所示，在A点可先参观区域1，也可先参观区域2或3，共有3种不同选法．每种选法中又有2×2×2×2=16种不同线路．

∴共有3×16=48种不同的参观路线．

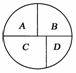
4．如右图所示，用五种不同的颜色分别给A、B、C、D四个区域涂色，相邻区域必须涂不同颜色，若允许同一种颜色多次使用，则不同的涂色方法共有(　)

A．180种　 　　　　　　　　　　　　　　　　　　　　　　　　　 B．120种

C．96种　 　　　　　　　　　　　　　　　　　　　　　　　　　　 D．60种

答案：A

解析：按区域分四步：第一步A区域有5种颜色可选；

第二步B区域有4种颜色可选；

第三步C区域有3种颜色可选；

第四步由于D区域可以重复使用区域A中已有过的颜色，故也有3种颜色可选用．由分步计数原理，共有5×4×3×3＝180(种)涂色方法．

3．从集合{1,2,3，…，10}中任意选出三个不同的数，使这三个数成等比数列，这样的等比数列的个数为(　)

A．3　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B．4

C．6　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．8

答案：D

解析：当公比为2时，等比数列可为1、2、4,2、4、8.

当公比为3时，等比数列可为1、3、9.

当公比为时，等比数列可为4、6、9.

同时，4、2、1和8、4、2,9、3、1,9、6、4也是等比数列，共8个．故选D.

2．某通讯公司推出一组手机卡号码，卡号的前七位数字固定，从“×××××××0000”到“×××××××9999”共10000个号码，公司规定：凡卡号的后四位中带数字“4”或“7”的一律作为优惠卡，则这组号码中“优惠卡”的个数为(　)

A．2000　 　　　　　　　　　　　　　　　　　　　　　　　　　　 B．4096

C．5904　 　　　　　　　　　　　　　　　　　　　　　　　　　　 D．8320

答案：C

解析：从反面考虑：后4位中不带数字“4”和“7”的一共有8×8×8×8＝4096个，∴带“4”或“7”的有10000－4096＝5904个．故选C.