
 对数函数的概念、图象和性质:
对数函数的概念、图象和性质:
①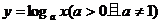 的定义域为
的定义域为 ,值域为
,值域为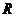 ;
;
② 的符号规律:同范围时值为正,异范围时值为负。
的符号规律:同范围时值为正,异范围时值为负。
③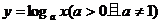 的单调性:
的单调性:
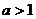 时,在
时,在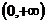 单增,
单增,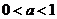 时,在
时,在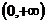 单减。
单减。
④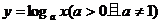 的图象特征:
的图象特征:
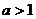 时,图象像一撇,过
时,图象像一撇,过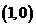 点,在
点,在 轴上方
轴上方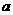 越大越靠近
越大越靠近 轴;
轴;
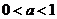 时,图象像一捺,过
时,图象像一捺,过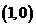 点,在
点,在 轴上方
轴上方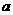 越小越靠近
越小越靠近 轴。
轴。
⑤“同正异负“法则:给定两个区间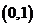 和
和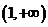 ,若
,若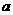 与
与 的范围处于同一个区间,则对数值大于零;否则若
的范围处于同一个区间,则对数值大于零;否则若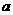 与
与 的范围分处两个区间,则对数值小于零.
的范围分处两个区间,则对数值小于零.
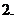 指数函数
指数函数 与对数函数
与对数函数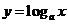 互为反函数;
互为反函数;
1.( 山东)函数
山东)函数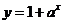
 的反函数的图象大致是
的反函数的图象大致是

(A) (B) (C) (D)
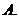


 (
( 湖北文)若函数
湖北文)若函数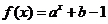 (
( ,且
,且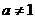 )的图象经过第二、三、四象限,则一定有
)的图象经过第二、三、四象限,则一定有 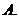
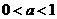 且
且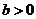 ;
; 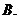
 且
且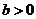

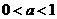 且
且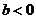 ;
;

 且
且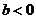
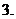 (
( 全国Ⅲ文)设
全国Ⅲ文)设 ,则
,则
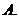
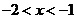
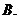


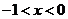

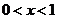
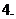 (
( 山东)已知集合
山东)已知集合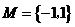 ,
, ,则
,则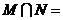
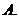
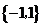
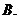
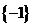



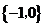
 (
( 北京)函数
北京)函数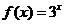 (
( ≤
≤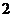 )的反函数的定义域为
)的反函数的定义域为
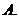

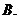





 (
( 江西)已知实数
江西)已知实数 、
、 满足等式
满足等式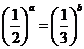 下列五个关系式
下列五个关系式
①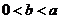 ;②
;②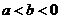 ;③
;③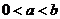 ;④
;④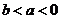 ;⑤
;⑤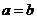
其中不可能成立的关系式有
 1个
1个  2个
2个  3个
3个  4个
4个
 (
( 山东)设函数
山东)设函数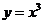 与
与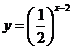 的图象的交点为
的图象的交点为 ,则
,则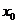 所在的区间是
所在的区间是





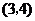
 (
( 全国Ⅲ理)已知函数
全国Ⅲ理)已知函数 是奇函数,则当
是奇函数,则当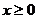 时,
时,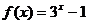 ,设
,设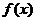 的反函数是
的反函数是 ,则
,则
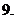 (
( 全国Ⅰ)设
全国Ⅰ)设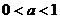 ,函数
,函数 ,则使
,则使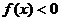 的
的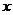 的取值范围是
的取值范围是
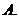

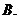




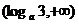
 (
(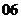 天津)如果函数
天津)如果函数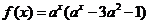 (
( 且
且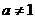 )在区间
)在区间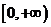 上
上
是增函数,那么实数 的取值范围为
的取值范围为

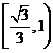

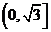


 1. 如图为指数函数
1. 如图为指数函数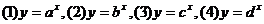 ,则
,则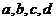 与
与 的大小关系为
的大小关系为
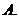
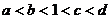
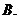
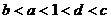



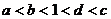
2.若函数 的图象与
的图象与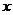 轴有交点,则实数
轴有交点,则实数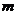 的范围是
的范围是
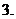 已知函数
已知函数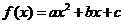
 ,满足
,满足 ,则
,则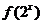 与
与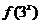 的大小关系是
的大小关系是 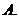
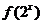
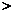
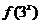
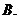
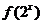
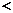
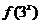

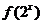 ≥
≥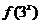

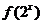 ≤
≤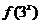
 若直线
若直线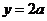 与函数
与函数 (
( 且
且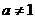 )的图象有两个公共点,则
)的图象有两个公共点,则 的范围是
的范围是
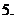 已知函数
已知函数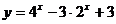 的值域为
的值域为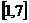 ,则
,则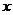 的范围是
的范围是
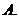

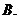
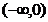

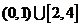

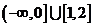
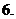 函数
函数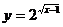 的定义域为
,值域为
的定义域为
,值域为
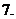 设
设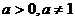 ,如果函数
,如果函数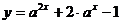 在
在 上的最大值为
上的最大值为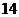 ,求
,求 的值
的值
 已知
已知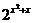 ≤
≤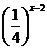 求函数
求函数 的值域
的值域
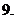 已知
已知
 .
.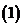 证明:
证明: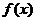 是定义域上的减函数;
是定义域上的减函数;
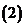 求
求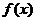 的值域.
的值域.
 已知
已知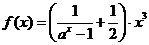 (
( ,且
,且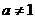 ).
).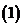 求
求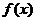 的定义域;
的定义域;
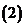 讨论
讨论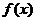 的奇偶性;
的奇偶性;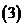 求
求 的范围,使
的范围,使 在定义域上恒成立.
在定义域上恒成立.
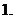 不等式
不等式 的解集为
的解集为
 函数
函数 的递减区间为 ;最大值是
的递减区间为 ;最大值是
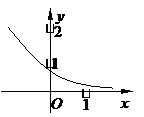 问题1.
问题1. (
( 福建)函数
福建)函数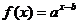 的图象如图,
的图象如图,
其中 、
、 为常数,则下列结论正确的是
为常数,则下列结论正确的是
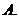
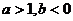
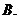
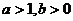

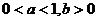

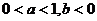
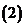 设
设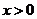 ,且
,且 (
( ,
,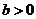 ),则
),则 与
与 的关系是
的关系是
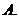
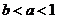
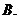
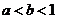

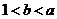

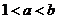
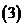 若函数
若函数 的图象不经过第一象限,则
的图象不经过第一象限,则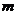 的取值范围是
的取值范围是
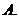

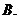
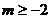

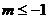

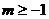
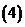 (
(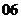 山东模拟)设
山东模拟)设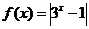 ,
,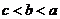 且
且 ,则下列关系式
,则下列关系式
一定成立的是 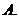

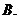
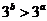

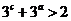


问题2.( 上海模拟)已知函数
上海模拟)已知函数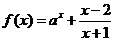
 ,
,
 证明函数
证明函数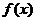 在
在 上为增函数;
上为增函数; 用反证法证明
用反证法证明 没有负数根.
没有负数根.
问题3.要使函数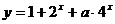 在
在 上
上 恒成立,求
恒成立,求 的取值范围.
的取值范围.
问题4.( 全国Ⅲ理)解方程:
全国Ⅲ理)解方程: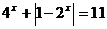
 指数方程,指数不等式:常要转化为同底数的形式,在利用指数函数的单调性求解;
指数方程,指数不等式:常要转化为同底数的形式,在利用指数函数的单调性求解;
 确定与指数有关的函数的单调性时,常要注意针对底数进行讨论;
确定与指数有关的函数的单调性时,常要注意针对底数进行讨论;
 要注意运用数形结合思想解决问题.
要注意运用数形结合思想解决问题.
|
|
 |
 |
|
图象 |
 |
 |
|
性质 |
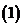 定义域: 定义域: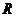 |
|
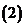 值域: 值域: |
||
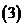 过点 过点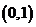 ,即 ,即 时, 时,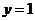 |
||
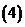 在 在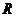 上是增函数 上是增函数 |
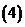 在 在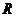 上是减函数 上是减函数 |
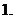
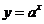 (
( 且
且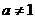 )的定义域为
)的定义域为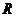 ,值域为
,值域为 .
.
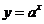 (
( 且
且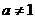 ) 的单调性:
) 的单调性: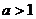 时,
时,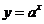 在
在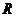 上为增函数;
上为增函数;
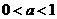 时,
时,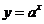 在
在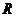 上是减函数.
上是减函数.
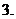
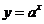 (
( 且
且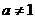 )的图像特征:
)的图像特征:
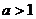 时,图象像一撇,过点
时,图象像一撇,过点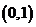 ,且在
,且在 轴左侧
轴左侧 越大,图象越靠近
越大,图象越靠近 轴(如图
轴(如图 );
);
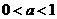 时,图象像一捺,过点
时,图象像一捺,过点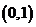 ,且在
,且在 轴左侧
轴左侧 越小,图象越靠近
越小,图象越靠近 轴(如图
轴(如图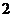 );
);
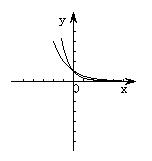
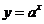 与
与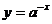 的图象关于
的图象关于 轴对称(如图
轴对称(如图 ).
).

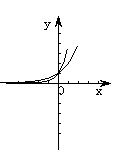 图
图 图
图 图
图
 (
( 全国Ⅲ文)解方程
全国Ⅲ文)解方程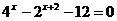
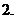 (
(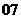 上海文)方程
上海文)方程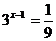 的解是
的解是
 (
( 上海)方程
上海)方程  的解是
的解是
 (
( 上海春)若
上海春)若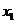 、
、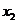 为方程
为方程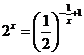 的两个实数解,则
的两个实数解,则
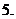 (
( 湖南文)若
湖南文)若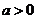 ,
, ,则
,则
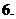 (
( 广东)函数
广东)函数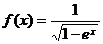 的定义域是
的定义域是
 (
( 全国Ⅱ) 设函数
全国Ⅱ) 设函数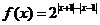 ,求使
,求使 ≥
≥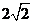 的
的 取值范围.
取值范围.
 (
( 湖北文)若
湖北文)若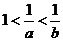 ,则下列结论中不正确的是
,则下列结论中不正确的是
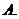
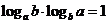
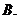
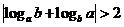
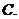


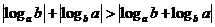
 (
( 北京)方程
北京)方程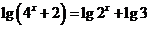 的解是
的解是
 (
( 辽宁文)方程
辽宁文)方程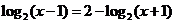 的解为
的解为
 (
( 上海文)方程
上海文)方程 的解是
的解是
 方程
方程 的解是
的解是
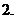 方程
方程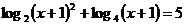 的解是
的解是
 设
设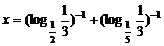 ,则
,则 属于区间
属于区间

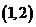
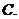
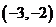


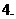 若
若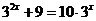 ,那么
,那么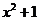 的值为
的值为
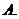
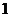

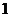 或
或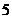
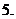 已知
已知 ,则
,则 的值为
的值为
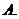
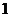
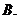
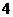
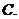
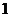 或
或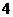

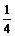 或
或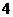
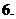 如果方程
如果方程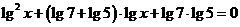 的两根为
的两根为 、
、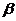 ,则
,则 的值是
的值是
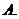
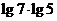
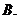
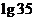
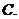
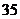


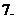
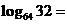 ;
; ,则
,则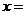
若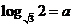 ,
,
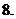
 的值为
的值为
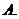
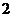
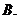
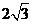
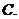




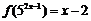 ,则
,则
 已知:
已知: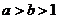 ,
,
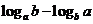 的值为
的值为
 求值或化简:
求值或化简: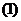
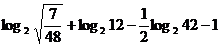 =
=
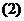
 =
=
 若
若 ,求
,求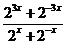 的值
的值
 已知
已知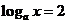 ,
,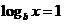 ,
,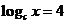 ,则
,则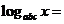
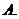
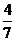
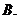
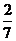
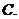
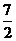

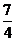
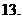 设
设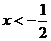 ,则
,则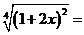
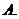

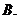

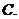
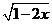


 已知:
已知: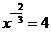 ,则
,则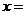
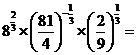
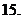 设
设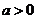 ,则
,则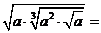
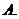
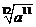
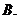
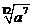
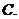


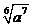
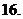 函数
函数 ,则
,则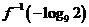 的值是
的值是
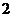
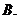
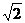
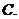


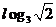

 若
若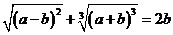 ,则有
,则有
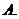
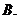
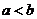
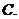


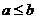
 已知
已知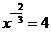 ,则
,则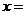
 求
求 的值.
的值.
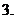 设
设 ,求
,求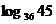 .
.
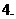 若
若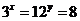 ,则
,则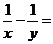
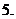 (
(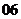 成都市诊断)
成都市诊断)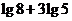 的值为
的值为 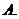



湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com