要得到的图象，只需将的图象

　 向左平移　 向右平移　 　向左平移　向右平移

如果函数的图象关于直线对称，则　　　　　

函数 的部分图象是

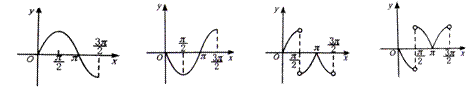
问题1． 已知函数.

用“五点法”画出它的图象；求它的振幅、周期和初相；

说明该函数的图象可由的图象经过怎样的变换而得到.

问题2．(海南)函数在区的简图是

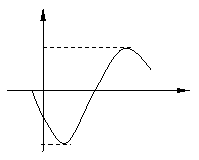(天津文)函数

的部分图象如图所示，则函数表达式为

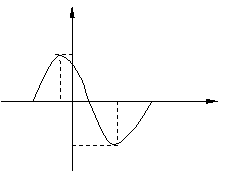
已知函数()

的一段图象如下图所示，求该函数的解析式．

问题3．将函数的周期扩大到原来的倍，再将函数图象左移，得到图象对应解析式是

(山东文)要得到函数的图象，只需将函数

的图象　　 向右平移个单位；向右平移个单位；

向左平移个单位；向左平移个单位

(山东)为了得到函数的图象，可以将函数的图象

向右平移个单位长度　　　　 　向右平移个单位长度

向左平移个单位长度　　　　 向左平移个单位长度

问题4．(福建)已知函数的最小正周期为，则

该函数的图象　 关于点对称　 关于直线对称

关于点对称　 .关于直线对称

(山东)已知函数，则下列判断正确的是　

　此函数的最小正周期为，其图象的一个对称中心是

　此函数的最小正周期为，其图象的一个对称中心是

　此函数的最小正周期为，其图象的一个对称中心是

此函数的最小正周期为，其图象的一个对称中心是

问题5．(陕西)设函数，其中向量，，，且的图象经过点．(Ⅰ)求实数的值；(Ⅱ)求函数的最小值及此时值的集合．

“五点法”画正弦、余弦函数和函数的简图，五个特殊点通常都是取三个平衡点，一个最高、一个最低点；

给出图象求的解析式的难点在于的确定，本质为待定系数法，基本方法是：①寻找特殊点(平衡点、最值点)代入解析式；②图象变换法，即考察已知图象可由哪个函数的图象经过变换得到的，通常可由平衡点或最值点确定周期，进而确定．

对称性:函数对称轴可由解出；对称

中心的横坐标是方程的解，对称中心的纵坐标为.( 即整体代换法)

函数对称轴可由解出；对称中心的纵坐标是方程的解，对称中心的横坐标为.( 即整体代换法)

函数对称中心的横坐标可由解出，对称中心的纵坐标为，函数不具有轴对称性.

时，，当时，有最大值，

当时,有最小值；时，与上述情况相反.

“五点法”画正弦、余弦函数和函数的简图.

函数的图象到函数的图象的两种主要途径．

掌握正弦、余弦、正切函数图象的对称轴或对称中心.

会由三角函数图象求出相应的解析式.

　(北京)若集合，则

　(上海)已知，，则

(陕西文)已知全集，集合，则集合等于

　(江西)若，且，

则中元素的个数为(　)　　　　　　　　 　　　　　　 　　　 　 　

(福建)已知，且，则的

范围是(　　 )　 　≤　　 　 　 　　 　　≥ 　　 　

(安徽文)设全集，集合，，则

等于(　　 ) 　　　

(福建文)已知全集且

则等于(　　 　)　　　

(辽宁文)设集合，则满足的集合的个数是

(湖北文)若是小于的正整数，，，则 　　　　　　 　　　　　　 　　　　

(重庆)已知，，则 ＝(　　 )　　 　　　　　{}

(全国Ⅱ文，满分分)

设，函数若的解集为，，

若，求实数的取值范围

7. 设，，已知，求

(选做，西安交大附中模拟)，求的值；

且，求的值；

，求的值.

6. 设集合, , 若, 则

实数的范围是(　　 ) ≥ 　　≤　 　

5．已知全集，子集，且，求实数

4．设含有个元素的集合的全部子集数为，其中由个元素组成的子集个数为，

则　　　　　　

3．设，，，且，

则　　　 ，