
 (
( 浙江)设集合
浙江)设集合 =
=
 |
| ,
, ,
, 是三角形的三边长
是三角形的三边长 ,
,
则 所表示的平面区域(不含边界的阴影部分)是
所表示的平面区域(不含边界的阴影部分)是
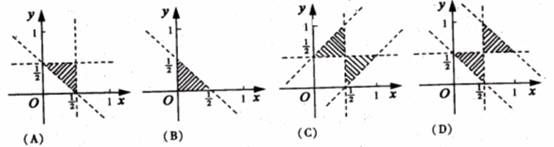
 (
( 天津文)设变量
天津文)设变量 满足约束条件
满足约束条件 则目标函数
则目标函数 的最大值为
的最大值为 







 (
( 湖北)已知平面区域
湖北)已知平面区域 由以
由以 、
、 、
、 为顶点的三角形内部和边界组成.若在区域
为顶点的三角形内部和边界组成.若在区域 上有无穷多个点
上有无穷多个点 可使目标函数
可使目标函数 取得最小值,则
取得最小值,则









 (
( 浙江)设
浙江)设 为实数,若
为实数,若 ,则
,则 的取值范围是
的取值范围是
 (
( 安徽文)如果点
安徽文)如果点 在平面区域
在平面区域 上,点
上,点 在曲线
在曲线 ,上,那么
,上,那么  最小值为
最小值为







 (
( 湖南)设集合
湖南)设集合 ,
, ,
, ,
,
 的取值范围是 ;
的取值范围是 ; 若
若 ,且
,且 的最大值为
的最大值为 ,则
,则 的值是
的值是
 (
( 江苏)设变量
江苏)设变量 满足约束条件
满足约束条件 ,则
,则 的最大值为
的最大值为
 (
( 四川)某厂生产甲产品每千克需用原料
四川)某厂生产甲产品每千克需用原料 和原料
和原料 分别为
分别为 千克,生产乙产品每千克需用原料
千克,生产乙产品每千克需用原料 和原料
和原料 分别为
分别为 千克。甲、乙产品每千克可获利润分别为
千克。甲、乙产品每千克可获利润分别为 元。月初一次性购进本月用原料
元。月初一次性购进本月用原料 、
、 各
各 千克。要计划本月生产甲、乙两种产品各多少千克才能使月利润总额达到最大。在这个问题中,设全月生产甲、乙两种产品分别为
千克。要计划本月生产甲、乙两种产品各多少千克才能使月利润总额达到最大。在这个问题中,设全月生产甲、乙两种产品分别为 千克、
千克、 千克,月利润总额为
千克,月利润总额为 元,那么,用于求使总利润
元,那么,用于求使总利润 最大的数学模型中,约束条件为
最大的数学模型中,约束条件为








 (
( 届高三重庆酉阳一中四检)已知
届高三重庆酉阳一中四检)已知 满足约束条件
满足约束条件 ,
,
则 的最大值为
的最大值为
 原点和点
原点和点 在直线
在直线 的两侧,则
的两侧,则 的取值范围是
的取值范围是
 如果实数
如果实数 、
、 满足
满足 , 目标函数
, 目标函数 的最大值为
的最大值为 , 最小值
, 最小值 ,那么实数
,那么实数 的值为
的值为 





 不存在
不存在
 (
( 届高三西安八校第一次月考)已知
届高三西安八校第一次月考)已知 ,则
,则 的最小值为
的最小值为
 (
( 苏州中学模拟)如图,目标函数
苏州中学模拟)如图,目标函数 的可行域为四边形
的可行域为四边形
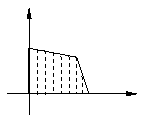 (含边界),若(
(含边界),若( )是该目标函数的最优解,则
)是该目标函数的最优解,则 的取值范围是
的取值范围是








 已知
已知 ,则
,则 是
是 的
的
 充分不必要条件
充分不必要条件 必要不充分条件
必要不充分条件 既不充分也不必要条件
既不充分也不必要条件 充要条件
充要条件
问题1. 不等式
不等式 表示的平面区域在直线
表示的平面区域在直线 的
的
 左上方
左上方  右上方
右上方  左下方
左下方  右下方
右下方
 (
( 全国Ⅰ)在坐标平面上,不等式组
全国Ⅰ)在坐标平面上,不等式组 所表示的平面区域的面积为
所表示的平面区域的面积为








 画出不等式组
画出不等式组 表示的平面区域,并回答下列问题:
表示的平面区域,并回答下列问题:
①指出 的取值范围;②平面区域内有多少个整点?(尽可能多种解法)
的取值范围;②平面区域内有多少个整点?(尽可能多种解法)
 已知点
已知点 、
、 在直线
在直线 的异侧,则
的异侧,则 的取值范围是
的取值范围是
问题2. (
( 湖南)已知点
湖南)已知点 在不等式组
在不等式组 表示的平面区域上运动,则
表示的平面区域上运动,则 的取值范围是
的取值范围是 







 (
( 辽宁)已知变量
辽宁)已知变量 满足约束条件
满足约束条件 则
则 的取值范围是
的取值范围是








 (
( 湖南)已知
湖南)已知 则
则 的最小值是
的最小值是
 (
( 重庆)已知变量
重庆)已知变量 满足约束条件:
满足约束条件: ≤
≤ ≤
≤ ,
, ≤
≤ ≤
≤ .若目标
.若目标
函数 (其中
(其中 )仅在点
)仅在点 处取得最大值,求
处取得最大值,求 的取值范围.
的取值范围.
问题3.制订投资计划时,不仅要考虑可能获得的利益,而且要考虑可能出现的亏损。
某投资人打算投资甲、乙两个项目.根据预测,甲、乙两个项目可能的最大盈利率分别为 和
和 ,可能的最大亏损率分别为
,可能的最大亏损率分别为 和
和 ,投资人计划投资金额不超过
,投资人计划投资金额不超过 万元,要求确保可能的资金亏损不超过
万元,要求确保可能的资金亏损不超过 万元.问投资人对甲、乙两项目各投资多少万元,才能使可能的盈利最大?
万元.问投资人对甲、乙两项目各投资多少万元,才能使可能的盈利最大?
 问题4.要将两种大小不同的钢板截成
问题4.要将两种大小不同的钢板截成 、
、 、
、 三种规格,每张钢板可同时截成三种规格的小钢板块数如左下表:
三种规格,每张钢板可同时截成三种规格的小钢板块数如左下表:
 |
 |
 |
 |
|
第一种钢板 |
 |
 |
 |
|
第二种钢板 |
 |
 |
 |
 二元一次不等式表示平面区域.
二元一次不等式表示平面区域.
 一般地,二元一次不等式
一般地,二元一次不等式 在平面直角坐标系中表示直线
在平面直角坐标系中表示直线 某一侧的所有点组成的平面区域(半平面)不含边界线;不等式
某一侧的所有点组成的平面区域(半平面)不含边界线;不等式 所表示的平面区域(半平面)包括边界线.
所表示的平面区域(半平面)包括边界线.
 判定不等式
判定不等式 (或
(或 )所表示的平面区域时,只要在直线
)所表示的平面区域时,只要在直线 的一侧任意取一点
的一侧任意取一点 ,将它的的坐标代入不等式,如果该点的坐标满足不等式,不等式就表示该点所在一侧的平面区域;如果不满足不等式,就表示这个点所在区域的另一侧平面区域。
,将它的的坐标代入不等式,如果该点的坐标满足不等式,不等式就表示该点所在一侧的平面区域;如果不满足不等式,就表示这个点所在区域的另一侧平面区域。
 由几个不等式组成的不等式组表示的平面区域是各个不等式所表示的平面区域的公共部分.
由几个不等式组成的不等式组表示的平面区域是各个不等式所表示的平面区域的公共部分.
另外:规律总结: ,(视“
,(视“ ”为“
”为“ ”,“
”,“ ”为“
”为“ ”),分别
”),分别
计算: 的符号与“
的符号与“ ”或“
”或“ ”的积;
”的积; 的符号与“
的符号与“ ”或“
”或“ ”的积; “左下负,右上正”.
”的积; “左下负,右上正”.
 线性规划问题的图解法:
线性规划问题的图解法:
 基本概念
基本概念
|
名 称 |
意
义 |
|
线性约束条件 |
由 的一次不等式(或方程)组成的不等式组,是对x,y的约束条件 的一次不等式(或方程)组成的不等式组,是对x,y的约束条件 |
|
目标函数 |
关于 的解析式 的解析式 |
|
线性目标函数 |
关于 的一次解析式 的一次解析式 |
|
可行解 |
满足线性约束条件的解 叫做可行解 叫做可行解 |
|
可行域 |
所有可行解组成的集合叫做可行域 |
|
最优解 |
使目标函数达到最大值或最小值的可行解 |
|
线性规划问题 |
求线性目标函数在线性约束条件下的最大值或最小值的问题 |
 用图解法解决线性规划问题的一般步骤
用图解法解决线性规划问题的一般步骤
① 设出所求的未知数;②列出约束条件(即不等式组);③建立目标函数;
④ 作出可行域;⑤运用图解法求出最优解.
 解法归类:
解法归类: 图解法;
图解法; 列表法;
列表法; 待定系数法;
待定系数法; 调整优值法;
调整优值法; 打网格线法.
打网格线法.
 交点定界法.
交点定界法.
 注意运用线性规划的思想解题.
注意运用线性规划的思想解题.
 (
( 北京)若直线
北京)若直线 :
: 与直线
与直线 的交点位于第一象限,
的交点位于第一象限,
则直线 的倾斜角的取值范围是
的倾斜角的取值范围是 







 (
( 全国文)直线
全国文)直线 关于
关于 轴对称的直线方程为
轴对称的直线方程为








 (
( 安徽春)已知直线
安徽春)已知直线 :
: ,
, :
: .若直线
.若直线 与
与 关于
关于 对
对
称,则 的方程为
的方程为







 (
( 上海)直线
上海)直线 关于直线
关于直线 对称的直线方程是
对称的直线方程是
 (
( 上海文)圆
上海文)圆 关于直线
关于直线 对称的圆的方程是
对称的圆的方程是








 方程
方程 表示的直线必经过点
表示的直线必经过点








 直线
直线 关于点
关于点 对称的直线方程是
对称的直线方程是








 曲线
曲线 关于直线
关于直线 对称的曲线方程是
对称的曲线方程是

 ,
, ,
, 仅有两个元素,则实数
仅有两个元素,则实数 的范围是
的范围是
 求经过直线
求经过直线 和
和 的交点,且在两坐标轴上的截距相等的直线方程
的交点,且在两坐标轴上的截距相等的直线方程
 已知
已知 的顶点为
的顶点为 ,
, 的平分线所在直线的方程分别是
的平分线所在直线的方程分别是 :
:
 与
与 :
: ,求
,求 边所在直线的方程.
边所在直线的方程.
 已知直线
已知直线 ,当
,当 变化时所得的直线都经过的定点为
变化时所得的直线都经过的定点为
 求证:不论
求证:不论 取何实数,直线
取何实数,直线 总通过一定点
总通过一定点
 求点
求点
 关于直线
关于直线 :
: 的对称点
的对称点 的坐标
的坐标
 已知:
已知: 与
与 ,
, 是对称的两点,求对称轴的方程
是对称的两点,求对称轴的方程
 光线沿直线
光线沿直线 :
: 射入,遇到直线
射入,遇到直线 :
: 反射,求反射光线所在的直线
反射,求反射光线所在的直线 的方程
的方程
 已知点
已知点 ,
, ,试在直线
,试在直线 :
: 上找一点
上找一点 ,使
,使 最小,并求出最小值.
最小,并求出最小值.
问题1.( 湖北联考)一条光线经过点
湖北联考)一条光线经过点 ,射在直线
,射在直线 :
: 上,
上,
反射后穿过点 .
. 求入射光线的方程;
求入射光线的方程; 求这条光线从点
求这条光线从点 到点
到点 的长度.
的长度.
问题2.求直线 :
: 关于直线
关于直线 :
: 对称的直线
对称的直线 的方程.
的方程.
问题3.根据下列条件,求直线的直线方程
 求通过两条直线
求通过两条直线 和
和 的交点,且到原点距离为
的交点,且到原点距离为 ;
;
 经过点
经过点 ,且与直线
,且与直线 平行;
平行;
 经过点
经过点 ,且与直线
,且与直线 垂直.
垂直.
问题4. 已知方程
已知方程 有一正根而没有负根,求实数
有一正根而没有负根,求实数 的范围
的范围
 若直线
若直线 :
: 与
与 :
: 的交点在第一象限,求
的交点在第一象限,求 的取值范围.
的取值范围.
 已知定点
已知定点 和直线
和直线 :
:

求证:不论 取何值,点
取何值,点 到直线
到直线 的距离不大于
的距离不大于
 点
点 关于
关于 轴的对称点的坐标为
轴的对称点的坐标为 ;关于
;关于 轴的对称点的坐标为
轴的对称点的坐标为 ;关于
;关于 的对称点的坐标为
的对称点的坐标为 ;关于
;关于 的对称点的坐标为
的对称点的坐标为 .
.
 点
点 关于直线
关于直线 的对称点的坐标的求法:
的对称点的坐标的求法:
 设所求的对称点
设所求的对称点 的坐标为
的坐标为 ,则
,则 的中点
的中点 一定在直线
一定在直线 上.
上.
 直线
直线 与直线
与直线 的斜率互为负倒数,即
的斜率互为负倒数,即
结论:点 关于直线
关于直线 :
: 对称点为
对称点为 ,
,
其中 ;曲线
;曲线 :
: 关于直线
关于直线 :
: 的对称曲线方程为
的对称曲线方程为 特别地,当
特别地,当 ,即
,即 的斜率为
的斜率为 时,点
时,点 关于直线
关于直线 :
: 对称点为
对称点为 ,即
,即 关于直线
关于直线 对称的点为:
对称的点为: ,曲线
,曲线 关于
关于 的对称曲线为
的对称曲线为
 直线
直线 关于直线
关于直线 的对称直线方程的求法:
的对称直线方程的求法:
①到角相等;②在已知直线上去两点(其中一点可以是交点,若相交)求这两点关于对称轴的对称点,再求过这两点的直线方程;③轨迹法(相关点法);④待定系数法,利用对称轴所在直线上任一点到两对称直线的距离相等,…
 点
点 关于定点
关于定点 的对称点为
的对称点为 ,曲线
,曲线 :
: 关于定点
关于定点 的对称曲线方程为
的对称曲线方程为 .
.
 直线系方程:
直线系方程:
 直线
直线 (
( 为常数,
为常数, 参数;
参数; 为参数,
为参数, 位常数).
位常数).
 过定点
过定点 的直线系方程为
的直线系方程为 及
及
 与直线
与直线 平行的直线系方程为
平行的直线系方程为 (
( )
)
 与直线
与直线 垂直的直线系方程为
垂直的直线系方程为
 过直线
过直线 和
和 的交点的直线系的方程为:
的交点的直线系的方程为: (不含
(不含 )
)
 (
( 全国)如果直线
全国)如果直线 与直线
与直线 平行,那么系数
平行,那么系数








 (
( 全国)两条直线
全国)两条直线 ,
, 垂直的充要条件是:
垂直的充要条件是:








 (
( 北京)“
北京)“ ”是“直线
”是“直线 与直线
与直线 相互垂直”的
相互垂直”的  充分必要条件;
充分必要条件;
 充分而不必要条件;
充分而不必要条件; 必要而不充分条件;
必要而不充分条件;  既不充分也不必要条件.
既不充分也不必要条件.
 (
( 京皖春)直线
京皖春)直线 和直线
和直线 的位置关系是
的位置关系是
 相交不垂直
相交不垂直  垂直
垂直  平行
平行  重合
重合
 (
( 全国Ⅱ)过点
全国Ⅱ)过点 且垂直于直线
且垂直于直线 的直线方程为
的直线方程为








 (
( 全国Ⅲ)已知过点
全国Ⅲ)已知过点 和
和 的直线与直线
的直线与直线 平行,则
平行,则
的值为 







 (
( 天津文)“
天津文)“ ”是“直线
”是“直线 平行于直线
平行于直线 ”的
”的
 充分而不必要条件
充分而不必要条件 必要而不充分条件
必要而不充分条件 充要条件
充要条件 既不充分也不必要条件
既不充分也不必要条件
 (
( 上海春)直线
上海春)直线 与直线
与直线 的夹角为
的夹角为
 (
( 浙江)点
浙江)点 到直线
到直线 的距离是
的距离是







 (
( 全国)已知点
全国)已知点 (
( )到直线
)到直线 :
: 的距离为
的距离为 ,则
,则 等于
等于








 (
( 全国文)已知两条直线
全国文)已知两条直线 :
: ,
, :
: ,其中
,其中 为实数,当这两条直线的夹角在
为实数,当这两条直线的夹角在 内变动时,
内变动时, 的取值范围是
的取值范围是







 (
( ,
, )
)
 已知直线
已知直线 :
: 和直线
和直线 :
: ,求满足下列条件的实数
,求满足下列条件的实数 的取值范围或取值:
的取值范围或取值:
 与
与 相交; ;
相交; ;

 ∥
∥ : ;
: ;
 ; ;
; ;
 与
与 重合;
重合;
 (
( 届高三北京海淀第一学期期末练习)若直线
届高三北京海淀第一学期期末练习)若直线 与直线
与直线
 平行,则实数
平行,则实数 的值为
的值为




 或
或

 或
或
 (
( 上海)设
上海)设 分别为
分别为 所对边长,则直线
所对边长,则直线 与直线
与直线
 的位置关系是:
的位置关系是: 平行
平行 重合
重合 垂直
垂直 相交但不垂直
相交但不垂直
 已知
已知 ,则
,则 的最小值是
的最小值是
 已知:
已知: 、
、 ,且
,且 ,求证:
,求证: ≥
≥
 若两平行线
若两平行线 与
与 之间的距离为
之间的距离为 ,则
,则
 直线
直线 在
在 轴和
轴和 轴上的截距分别为
轴上的截距分别为 和
和 ,直线
,直线 的方程为
的方程为 ,直线
,直线 与
与 的夹角为
的夹角为 ,则
,则 的值为
的值为
 已知一直线
已知一直线 被两直线
被两直线 :
: 和
和 :
: 截得的
截得的
线段长为 ,且
,且 过点
过点 ,求直线
,求直线 的方程.
的方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com