
|
定义 |
 平面内到两个定点 平面内到两个定点 的距离之和等于定长( 的距离之和等于定长( )的点的轨迹 )的点的轨迹 平面内到定点 平面内到定点 与到定直线 与到定直线 的距离之比等于常数 的距离之比等于常数 ( ( )的点的轨迹 )的点的轨迹 |
||
|
方程 |
标准方程 |
椭圆 : : ( ( ); ); |
椭圆  : : (  ); ); |
|
参数方程 |
 |
||
|
图形 |
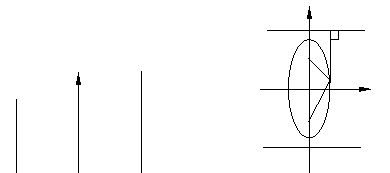 |
|
|
|
几何性质 |
焦点坐标 |
 , , |
 , , |
|
顶点 |
 , , ; ;  , , ; ; |
 , , ; ; , , ; ; |
|
|
范围 |
 ≤ ≤ , , ≤ ≤ ; ; |
 ≤ ≤ , , ≤ ≤ ; ; |
|
|
准线 |
 : : , , : : |
 : : , , : : |
|
焦半径 |
 , , |
 , , |
|
|
对称性 |
关于 轴均对称,关于原点中心对称; 轴均对称,关于原点中心对称; |
||
|
离心率 |
 |
||
 的关系 的关系 |
 |
||
焦点三角形 的面积: 的面积: ( ( , , 为短半轴长) 为短半轴长) |
 (
( 天津)若
天津)若 为圆
为圆 的弦
的弦 的中点,则直线
的中点,则直线 的方程是
的方程是








 (
( 湖北文)两个圆
湖北文)两个圆 :
: 与
与

的公切线有且仅有 
 条
条
 条
条
 条
条
 条
条
 (
( 江西)“
江西)“ ”是“直线
”是“直线 圆
圆 相切”的
相切”的
 充分不必要条件
充分不必要条件 必要不充分条件
必要不充分条件 充要条件
充要条件 既不充分又不必要条件
既不充分又不必要条件
 (
( 全国Ⅰ)设直线
全国Ⅰ)设直线 过点
过点 ,且与圆
,且与圆 相切,则
相切,则 的斜率是
的斜率是








 (
( 北京)从原点向圆
北京)从原点向圆 作两条切线,则该圆夹在两条切线间的
作两条切线,则该圆夹在两条切线间的
劣弧长为 







 (
( 全国Ⅰ文)从圆
全国Ⅰ文)从圆 外一点
外一点 向这个圆作两条切线,
向这个圆作两条切线,
则两切线夹角的余弦值为







 (
( 湖南文)圆
湖南文)圆 上的点到直线
上的点到直线 的最大距离与最小
的最大距离与最小
距离的差是 







 (
( 天津文)已知两圆
天津文)已知两圆 和
和 相交于
相交于 两点,
两点,
则直线 的方程是
的方程是
 (
( 山东)与直线
山东)与直线 和曲线
和曲线 都相切的半径最小的圆的标准方程是
都相切的半径最小的圆的标准方程是
 (
( 湖南)圆心为
湖南)圆心为 且与直线
且与直线 相切的圆的方程是
相切的圆的方程是
 (
( 江西)已知圆
江西)已知圆 :
: ,
,
直线 :
: ,下面四个命题:
,下面四个命题:
 对任意实数
对任意实数 与
与 ,直线
,直线 和圆
和圆 相切;
相切;
 对任意实数
对任意实数 与
与 ,直线
,直线 和圆
和圆 有公共点;
有公共点;
 对任意实数
对任意实数 ,必存在实数
,必存在实数 ,使得直线
,使得直线 与和圆
与和圆 相切
相切
 对任意实数
对任意实数 ,必存在实数
,必存在实数 ,使得直线
,使得直线 与和圆
与和圆 相切
相切
其中真命题的代号是 (写出所有真命题的代号)
 (
( 湖南) 若圆
湖南) 若圆 上至少有三个不同的点到直线
上至少有三个不同的点到直线 的距离为
的距离为 ,则直线
,则直线 的倾斜角的取值范围是
的倾斜角的取值范围是








 (
( 湖北文)由直线
湖北文)由直线 上的一点向圆
上的一点向圆 引切线,则切线长的最小值为
引切线,则切线长的最小值为







 (
( 安徽文)若圆
安徽文)若圆 的圆心到直线
的圆心到直线 的距离为
的距离为 ,则
,则 的值为
的值为 
 或
或



 或
或

 或
或
 (
( 湖北)若直线
湖北)若直线 与圆
与圆 相切,则
相切,则 的值为
的值为
 (
( 辽宁)已知点
辽宁)已知点 ,
,
 是抛物线
是抛物线
 上的两个动点,
上的两个动点, 是坐标原点,向量
是坐标原点,向量 ,
, 满足
满足 .设圆
.设圆 的方程为
的方程为
 证明线段
证明线段 是圆
是圆 的直径;
的直径;
 当圆
当圆 的圆心到直线
的圆心到直线 的距离的最小值为
的距离的最小值为 时,求
时,求 的值.
的值.
 直线
直线 与圆
与圆 在第一象限内有两个不同交点,则
在第一象限内有两个不同交点,则 的取值范围是
的取值范围是








 (
( 北京东城)
北京东城) 曲线
曲线 :
: (
( 为参数,
为参数, )上任意一点,
)上任意一点,
则 的最大值是
的最大值是 







 (
( 德州一模)若直线
德州一模)若直线 与曲线
与曲线 (
( ),有两个不同的交点,则实数
),有两个不同的交点,则实数 的取值范围是
的取值范围是
 两圆为:
两圆为: ,
, ,则
,则
 两圆的公共弦所在的直线方程为
两圆的公共弦所在的直线方程为
 两圆的内公切线方程为
两圆的内公切线方程为
 两圆的外公切线方程为
两圆的外公切线方程为
 以上都不对
以上都不对
 已知点
已知点 是圆
是圆 内一点,直线
内一点,直线 是以
是以 为中点的弦所在的直线,直线
为中点的弦所在的直线,直线 的方程是
的方程是 ,那么
,那么

 且
且 与圆
与圆 相切
相切 
 且
且 与圆
与圆 相切
相切

 且
且 与圆
与圆 相离
相离 
 且
且 与圆
与圆 相离
相离
 若半径为
若半径为 的动圆与圆
的动圆与圆 相切,则动圆圆心的轨迹方程是
相切,则动圆圆心的轨迹方程是
 圆
圆 上到直线
上到直线 的距离为
的距离为 的点共有 个
的点共有 个
 圆
圆 上的动点
上的动点 到直线
到直线 距离的最小值为
距离的最小值为
 (
( 北京春)已知直线
北京春)已知直线 (
( )与圆
)与圆 相切,则三条边长分别为
相切,则三条边长分别为 的三角形
的三角形 是锐角三角形
是锐角三角形 是直角三角形
是直角三角形 是钝角三角形
是钝角三角形 不存在
不存在
 (
( 届高三北京海淀第二学期期末练习)将圆
届高三北京海淀第二学期期末练习)将圆 按向量
按向量 平移后,恰好与直线
平移后,恰好与直线 相切,则实数
相切,则实数 的值为
的值为








 (
( 重庆模拟)已知
重庆模拟)已知 :
: ,
, :
: ,两圆的内公
,两圆的内公
切线交于 点,外公切线交于
点,外公切线交于 点,若
点,若 ,则
,则 等于
等于 







 已知圆
已知圆 的圆心在曲线
的圆心在曲线 上,圆
上,圆 与
与 轴相切,又与另一圆
轴相切,又与另一圆
相外切,求圆 的方程.
的方程.
 由点
由点 引圆
引圆 的割线
的割线 ,交圆于
,交圆于 两点,使
两点,使 的面积为
的面积为
( 为原点),求直线
为原点),求直线 的方程。
的方程。
 点
点 是圆
是圆 内的定点,点
内的定点,点 是这个圆上的两个动点,若
是这个圆上的两个动点,若 ,求
,求 中点
中点 的轨迹方程,并说明它的轨迹是什么曲线。
的轨迹方程,并说明它的轨迹是什么曲线。
 已知圆
已知圆 与直线
与直线 相交于
相交于 两点,
两点, 为原点,
为原点,
若 ,求实数
,求实数 的值.
的值.
 设圆上的点
设圆上的点 关于直线
关于直线 的对称点仍在圆上,且与直线
的对称点仍在圆上,且与直线 相交的弦长为
相交的弦长为 ,求圆的方程。
,求圆的方程。
 过点
过点 作圆
作圆 的两条切线,切点分别为
的两条切线,切点分别为 ;求:
;求:
 经过圆心
经过圆心 ,切点
,切点 这三点圆的方程;
这三点圆的方程; 直线
直线 的方程;
的方程; 线段
线段 的长。
的长。
问题1. (
( 全国Ⅲ)圆心为
全国Ⅲ)圆心为 且与直线
且与直线 相切的圆
相切的圆
 (
( 全国)圆
全国)圆 在点
在点 处的切线方程为
处的切线方程为 







 过点
过点 的圆
的圆 的切线方程是
的切线方程是
 (
( 全国Ⅰ)已知直线
全国Ⅰ)已知直线 过点
过点 ,当直线
,当直线 与圆
与圆 有两个交点时,其斜率
有两个交点时,其斜率 的取值范围是
的取值范围是







 (
( 届高三广东部分重点中学联考)过点
届高三广东部分重点中学联考)过点 引圆
引圆 的弦,
的弦,
则所作的弦中最短的弦长为 







 已知直线
已知直线 :
: 与曲线
与曲线 :
: 有两个公共点,求
有两个公共点,求 的取值范围.
的取值范围.
问题2.已知直线 :
: 和圆
和圆 ;
;

 时,证明
时,证明 与
与 总相交;
总相交; 
 取何值时,
取何值时, 被
被 截得弦长最短,求此弦长.
截得弦长最短,求此弦长.
问题3.已知圆 :
: 与
与 :
:
相交于 两点,
两点, 求公共弦
求公共弦 所在的直线方程;
所在的直线方程;
 求圆心在直线
求圆心在直线 上,且经过
上,且经过 两点的圆的方程;
两点的圆的方程;
 求经过
求经过 两点且面积最小的圆的方程.
两点且面积最小的圆的方程.
问题4.( 届高三桐庐中学月考)已知圆
届高三桐庐中学月考)已知圆 方程为:
方程为: .
. 直线
直线 过点
过点 ,且与圆
,且与圆 交于
交于 、
、 两点,若
两点,若 ,求直线
,求直线 的方程;
的方程; 过圆
过圆 上一动点
上一动点 作平行于
作平行于 轴的直线
轴的直线 ,设
,设 与
与 轴的交点为
轴的交点为 ,若向量
,若向量 ,求动点
,求动点 的轨迹方程,并说明此方程表示的曲线。
的轨迹方程,并说明此方程表示的曲线。
①直线与圆的位置关系
 将直线方程代入圆的方程得到一元二次方程,设它的判别式为
将直线方程代入圆的方程得到一元二次方程,设它的判别式为 ,圆的半径为
,圆的半径为 ,圆心
,圆心 到直线
到直线 的距离为
的距离为 ,则直线与圆的位置关系满足以下关系:
,则直线与圆的位置关系满足以下关系:
|
位置关系 |
相切 |
相交 |
相离 |
|
几何特征 |
 |
 |
 |
|
代数特征 |
 |
 |
 |
 直线截圆所得弦长的计算方法:①利用弦长计算公式:设直线
直线截圆所得弦长的计算方法:①利用弦长计算公式:设直线 与圆相交于
与圆相交于 ,
, 两点,则弦
两点,则弦
 ;
;
②利用垂径定理和勾股定理: (其中
(其中 为圆的半径,
为圆的半径, 直线到圆心的距离).
直线到圆心的距离).
②圆与圆的位置关系:设两圆的半径分别为 和
和 ,圆心距为
,圆心距为 ,则两圆的位置关系满足以下关系:
,则两圆的位置关系满足以下关系:
|
位置关系 |
外离 |
外切 |
相交 |
内切 |
内含 |
|
几何特征 |
 |
 |
 |
 |
 |
|
代数特征 |
无实数解 |
一组实数解 |
两组实数解 |
一组实数解 |
无实数解 |
 (
( 全国文)曲线
全国文)曲线 关于
关于
 直线
直线 轴对称
轴对称 直线
直线 轴对称
轴对称 点
点 中心对称
中心对称 点
点 中心对称
中心对称
 (
( 上海)将参数方程
上海)将参数方程 (
( 为参数)化为普通方程,所得方程是
为参数)化为普通方程,所得方程是
 (
( 重庆)圆
重庆)圆 关于原点
关于原点 对称的圆的方程为
对称的圆的方程为








 圆
圆 关于直线
关于直线 对称的圆的方程是
对称的圆的方程是 







 (
( 重庆文)若
重庆文)若 ,则
,则 的最大值是
的最大值是
 圆
圆 的圆心和半径分别是
的圆心和半径分别是

 ;
;

 ;
;

 ;
; ;
; 
 ;
;
 方程
方程 表示圆,则
表示圆,则 的取值范围是
的取值范围是








 以两点
以两点 和
和 为直径端点的圆的方程是
为直径端点的圆的方程是









 且
且 是方程
是方程 表示圆的
表示圆的
 充分非必要条件
充分非必要条件 必要非充分条件
必要非充分条件
 充要条件
充要条件 既非充分也非必要条件
既非充分也非必要条件
 (
( 南京市质检)已知圆
南京市质检)已知圆 关于直线
关于直线 成轴对称,
成轴对称,
则
 圆
圆 关于直线
关于直线 对称的圆的方程是
对称的圆的方程是








 已知向量
已知向量 ,
, ,
, ,则
,则 与
与 的夹角是
的夹角是
 直线
直线 与直线
与直线 的交点在圆
的交点在圆 上,则
上,则
 已知曲线
已知曲线 ,其中
,其中 ;
;
 求证:曲线
求证:曲线 都是圆,并且圆心在同一条直线上;
都是圆,并且圆心在同一条直线上;
 证明:曲线
证明:曲线 过定点;
过定点; 若曲线
若曲线 与
与 轴相切,求
轴相切,求 的值;
的值;
问题1. 求满足下列各条件圆的方程:
 以
以 ,
, 为直径的圆;
为直径的圆;  与
与 轴均相切且过点
轴均相切且过点 的圆;
的圆;
 求经过
求经过 ,
, 两点,圆心在直线
两点,圆心在直线 上的圆的方程;
上的圆的方程;
 经过两已知圆
经过两已知圆 :
: 和
和 :
: 的交点,
的交点,
且圆心在直线 :
: 上的圆的方程.
上的圆的方程.
问题2.已知实数 、
、 满足方程
满足方程 .
. 求
求 的最大值和最小值;
的最大值和最小值;
 求
求 的最小值;
的最小值; 求
求 的最大值和最小值.
的最大值和最小值.
问题3. (
( 盐城二模)已知
盐城二模)已知 (
( ,
, 为坐标原点),向量
为坐标原点),向量 满足
满足 ,则动点
,则动点 的轨迹方程是
的轨迹方程是
 平面上两点
平面上两点 、
、 ,在圆
,在圆 :
: 上取一点
上取一点 ,
,
求使 取得最小值时点
取得最小值时点 的坐标.
的坐标.
问题4.( 北京春)设
北京春)设 ,
, (
( )为两定点,动点
)为两定点,动点 到点
到点 的距离与到点
的距离与到点 的距离的比为定值
的距离的比为定值 (
( ),求
),求 点的轨迹.
点的轨迹.
 圆心为
圆心为 ,半径为
,半径为 的圆的标准方程为:
的圆的标准方程为: .特殊地,当
.特殊地,当 时,圆心在原点的圆的方程为:
时,圆心在原点的圆的方程为: .
.
 圆的一般方程
圆的一般方程 ,圆心为点
,圆心为点 ,半径
,半径
 ,其中
,其中 .
.
 二元二次方程
二元二次方程 ,表示圆的方程的充要条件是:
,表示圆的方程的充要条件是:
① 项
项 项的系数相同且不为
项的系数相同且不为 ,即
,即 ;②没有
;②没有 项,即
项,即 ;
;
③ .
.
 圆
圆 :
: 的参数方程为
的参数方程为 (
( 为参数).特殊地,
为参数).特殊地, 的参数方程为
的参数方程为 (
( 为参数).
为参数).
 圆系方程:过圆
圆系方程:过圆 :
: 与圆
与圆 :
:
交点的圆系方程是 (不含圆
(不含圆 ),
),
当 时圆系方程变为两圆公共弦所在直线方程.
时圆系方程变为两圆公共弦所在直线方程.
 (
( 福建)不等式
福建)不等式 的解集是( )
的解集是( )








 (
( 天津)不等式
天津)不等式 ≥
≥ 的解集为( )
的解集为( )








 (
( 江西)若不等式
江西)若不等式 对于一切
对于一切
 恒成立,
恒成立,
则 的最小值是
的最小值是 







 (
( 福建)已知全集
福建)已知全集 且
且
则 等于( )
等于( )







 (
( 天津理)解关于
天津理)解关于 的不等式
的不等式

 (
( 四川)已知集合
四川)已知集合 ,
, 则集合
则集合

 (
(





 (
( 山东文)当
山东文)当 时,不等式
时,不等式 恒成立,则
恒成立,则 的范围是
的范围是
 (
( 浙江)已知函数
浙江)已知函数 和
和 的图象关于原点对称,且
的图象关于原点对称,且
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)解不等式 ≥
≥

 (
( 全国Ⅱ文
全国Ⅱ文 ,满分
,满分 分)(见
分)(见 ,
, )
)
设 ,函数
,函数 若
若 的解集为
的解集为 ,
, ,
,
若 ,求实数
,求实数 的取值范围
的取值范围
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com