
问题1. (
( 全国Ⅱ)
全国Ⅱ) 的展开式中常数项为 (用数字作答).
的展开式中常数项为 (用数字作答).
 求
求 展开式中
展开式中 的系数(要求用两种方法解答).
的系数(要求用两种方法解答).
 求
求 展开式中系数最大的项
展开式中系数最大的项
 求
求 展开所得
展开所得 的多项式中,系数为有理数的项数
的多项式中,系数为有理数的项数
问题2. 已知
已知 ,
,
则
 (
( 安徽文)已知
安徽文)已知 ,
,
则 的值等于
.
的值等于
.
 (
( 浙江)若多项式
浙江)若多项式 ,则
,则








 (
( 天津)设
天津)设 ,则
,则
问题3. 求
求 的近似值(精确到
的近似值(精确到 )
)
 已知
已知 能被
能被 整除,则最小值
整除,则最小值
问题4. 求证:
求证: ≤
≤
 (
( );
); 你能把不等式中的上限
你能把不等式中的上限 变得更小些吗?
变得更小些吗?
 二项式定理及其特例:
二项式定理及其特例:

 ,
,



 二项展开式的通项公式:
二项展开式的通项公式:


 常数项、有理项和系数最大的项:
常数项、有理项和系数最大的项:
 求常数项、有理项和系数最大的项时,要根据通项公式讨论对
求常数项、有理项和系数最大的项时,要根据通项公式讨论对 的限制;求有理项时要注意到指数及项数的整数性.
的限制;求有理项时要注意到指数及项数的整数性.
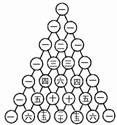
 二项式系数表(杨辉三角)
二项式系数表(杨辉三角)
 展开式的二项式系数,当
展开式的二项式系数,当 依次取
依次取 …时,二项式系数表,表中每行两端都是
…时,二项式系数表,表中每行两端都是 ,除
,除 以外的每一个数都等于它肩上两个数的和.
以外的每一个数都等于它肩上两个数的和.
 二项式系数的性质:
二项式系数的性质:
 展开式的二项式系数是
展开式的二项式系数是 ,
, ,
, ,…,
,…, .
. 可以看成以
可以看成以 为自变量的函数
为自变量的函数 ,定义域是
,定义域是 ,例当
,例当 时,其图象是
时,其图象是 个孤立的点(如图)
个孤立的点(如图)

 对称性.
对称性.
与首末两端“等距离”的两个二项式系数相等( ).直线
).直线 是图象的对称轴.
是图象的对称轴.
 增减性与最大值:
增减性与最大值:
当 是偶数时,中间一项
是偶数时,中间一项 取得最大值;当
取得最大值;当 是奇数时,中间两项
是奇数时,中间两项 ,
, 取得最大值.
取得最大值.
 各二项式系数和:∵
各二项式系数和:∵ ,
,
令 ,则
,则
 在使用通项公式
在使用通项公式 时,要注意:
时,要注意:
 通项公式是表示第
通项公式是表示第 项,而不是第
项,而不是第 项.
项. 展开式中第
展开式中第 项的二项式系数
项的二项式系数 与第
与第 项的系数不同.
项的系数不同. 通项公式中含有
通项公式中含有 五个元素,只要知道其中的四个元素,就可以求出第五个元素.在有关二项式定理的问题中,常常遇到已知这五个元素中的若干个,求另外几个元素的问题,这类问题一般是利用通项公式,把问题归纳为解方程(或方程组).这里必须注意
五个元素,只要知道其中的四个元素,就可以求出第五个元素.在有关二项式定理的问题中,常常遇到已知这五个元素中的若干个,求另外几个元素的问题,这类问题一般是利用通项公式,把问题归纳为解方程(或方程组).这里必须注意 是正整数,
是正整数, 是非负整数且
是非负整数且 ≤
≤ .
.  证明组合恒等式常用赋值法.
证明组合恒等式常用赋值法. 要正确理解二项式定理,准确地写出二项式的展开式.
要正确理解二项式定理,准确地写出二项式的展开式. 要注意区分项的系数与项的二项式系数.
要注意区分项的系数与项的二项式系数.  二项式展开式系数可用通项公式及组合知识.
二项式展开式系数可用通项公式及组合知识.
 用二项式定理进行近似运算,关键是恰当地舍取不影响精度的项,一般地:当
用二项式定理进行近似运算,关键是恰当地舍取不影响精度的项,一般地:当
很小时,有 .
.
 (
( 福建)某校高二年级共有六个班级,现从外地转入
福建)某校高二年级共有六个班级,现从外地转入 名学生,要安排到该年级的两个班级且每班安排
名学生,要安排到该年级的两个班级且每班安排 名,则不同的安排方案种数为
名,则不同的安排方案种数为








 (
( 福建文)某通讯公司推出一组手机卡号码,卡号的前七位数字固定,从“
福建文)某通讯公司推出一组手机卡号码,卡号的前七位数字固定,从“ ”到“
”到“ ”共
”共 个号码.公司规定:凡卡号的后四位带有数字“
个号码.公司规定:凡卡号的后四位带有数字“ ”或“
”或“ ”的一律作为“优惠卡”,则这组号码中“优惠卡”的个数为
”的一律作为“优惠卡”,则这组号码中“优惠卡”的个数为








 (
( 四川)用数字
四川)用数字 可以组成没有重复数字,并且比
可以组成没有重复数字,并且比 大的五位偶数
大的五位偶数
共有 
 个
个 
 个
个 
 个
个 
 个
个
 (
( 北京文)某城市的汽车牌照号码由
北京文)某城市的汽车牌照号码由 个英文字母后接
个英文字母后接 个数字组成,其中
个数字组成,其中 个数字互不相同的牌照号码共有
个数字互不相同的牌照号码共有
 个
个 
 个
个 
 个
个 
 个
个
 (
( 湖北)已知直线
湖北)已知直线 (
( 是非零常数)与圆
是非零常数)与圆 有公共点,且公共点的横坐标和纵坐标均为整数,那么这样的直线共有
有公共点,且公共点的横坐标和纵坐标均为整数,那么这样的直线共有

 条
条 
 条
条 
 条
条 
 条
条
 (
( 上海文)如果一条直线与一个平面垂直,那么,称此直线与平面构成一个“正交线面对”. 在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是
上海文)如果一条直线与一个平面垂直,那么,称此直线与平面构成一个“正交线面对”. 在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是 







 (
( 北京东城区模拟)组合数
北京东城区模拟)组合数
 (
( 昆明一模)如图,
昆明一模)如图, 为海上的四个小岛,要建三座桥,将这四个小岛连接起来,则不同的建桥方法共有
为海上的四个小岛,要建三座桥,将这四个小岛连接起来,则不同的建桥方法共有 
 种
种 
 种
种 
 种
种 
 种
种
 (
( 届高三湖南省十二校一联)如图,正五边形
届高三湖南省十二校一联)如图,正五边形
 中,若把顶点
中,若把顶点 染上红、黄、绿
染上红、黄、绿
三种颜色中的一种,使得相邻顶点所染颜色不相同,
则不同的染色方法共有 种 .
 (
( 湖北八校二联)用四种不同的颜色给正方体
湖北八校二联)用四种不同的颜色给正方体 的六个面染色,
的六个面染色,
要求四种颜色用完,且相邻两个面涂不同的颜色,则所有不同的涂色方法共有

 种
种 
 种
种

 种
种 
 种
种
 某人用
某人用 步恰好上完
步恰好上完 个台阶,则有
种不同上法.
个台阶,则有
种不同上法.
 个人站成一排,男女相间有
种排法,如果其中某三人站在一起,另外四人排在一起有
种排法,若其中甲乙之间各一人有
种排法.
个人站成一排,男女相间有
种排法,如果其中某三人站在一起,另外四人排在一起有
种排法,若其中甲乙之间各一人有
种排法.

 下面是高考第一批录取的一份志愿表:
下面是高考第一批录取的一份志愿表:
现有 所重点院校,每所重点院校有
所重点院校,每所重点院校有 个
个
专业是你较为满意的选择,如果表格填满
且规定学校没有重复,同一学校的专业也
没有重复,不同的填写方法的种数是:








 一个三位数
一个三位数 称为“凹数”,如果该三位数同时满足
称为“凹数”,如果该三位数同时满足 且
且 ,那么所有不同的
,那么所有不同的
“凹数”的个数是
 (
( 雅礼中学月考)已知
雅礼中学月考)已知 ,从
,从 到
到 的映射
的映射 满足:①
满足:① ≤
≤
≤ ≤
≤ ≤
≤ ;②
;② 的象有且只有
的象有且只有 个,则适合条件的映射
个,则适合条件的映射 的个数是
的个数是








问题1. 填空:①已知
填空:①已知 ,
, ,则
,则
 ;
;
②已知
 ,则
,则 ;③已知
;③已知 ,则
,则
 计算:①
计算:① ; ②
; ②
问题2. (
( 北京)记者要为
北京)记者要为 名志愿者和他们帮助的
名志愿者和他们帮助的 为老人拍照,要求排成一排,
为老人拍照,要求排成一排, 位老人相邻但不排在两端,不同的排法共有
位老人相邻但不排在两端,不同的排法共有
 种
种
 种
种
 种
种
 种
种
 (
( 全国Ⅰ)安排
全国Ⅰ)安排 位工作人员在
位工作人员在 月
月 日到
日到 月
月 日值班,每人值班一天,其中甲、乙二人都不能安排在
日值班,每人值班一天,其中甲、乙二人都不能安排在 月
月 日和
日和 日,不同的安排方法共有 种。(用数字作答)
日,不同的安排方法共有 种。(用数字作答)

 个人站成一排,其中
个人站成一排,其中 互不相邻且
互不相邻且 也互不相邻的排法有多少种?
也互不相邻的排法有多少种?
问题3. (
( 江苏)今有
江苏)今有 个红球、
个红球、 个黄球、
个黄球、 个白球,同色球不加以区分,
个白球,同色球不加以区分,
将这 个球排成一列有 种不同的方法(用数字作答).
个球排成一列有 种不同的方法(用数字作答).
 (
( 湖北联考)
湖北联考) 本不同的书,平均分成三堆,每堆两本,有
本不同的书,平均分成三堆,每堆两本,有 种不同的分法;
种不同的分法;
若分成三堆,有两堆各 本,另一堆
本,另一堆 本,有
本,有 种不同的分法,则
种不同的分法,则
问题4. (
( 陕西)安排
陕西)安排 名支教教师去
名支教教师去 所学校任教,每校至多
所学校任教,每校至多 人,则不同的分配方案共有
种.(用数字作答)
人,则不同的分配方案共有
种.(用数字作答)
 (
( 陕西)某校从
陕西)某校从 名教师中选派
名教师中选派 名教师同时去
名教师同时去 个边远地区支教(每地
个边远地区支教(每地 人),其中
人),其中
甲和乙不同去,甲和丙只能同去或同不去,则不同的选派方案共有 种
 (
( 辽宁)有两排座位,前排
辽宁)有两排座位,前排 个座位,后排
个座位,后排 个座位,现安排
个座位,现安排 人就座,
人就座,
规定前排中间的 个座位不能坐,并且这
个座位不能坐,并且这 人不左右相邻,那么不同排法的种数是
人不左右相邻,那么不同排法的种数是








问题5.按下列要求分配 本不同的书,各有多少种不同的分配方式:
本不同的书,各有多少种不同的分配方式:
 如果每人得
如果每人得 本有多少种不同的分法?
本有多少种不同的分法?
 如果甲得
如果甲得 本,乙得
本,乙得 本,丙得
本,丙得 本有多少种分法?
本有多少种分法?
 如果一人得
如果一人得 本,一人得
本,一人得 本,一人得
本,一人得 本有多少种分法?
本有多少种分法?
 平均分成三堆,每堆
平均分成三堆,每堆 本有多少种分法?
本有多少种分法?
问题6.  五个人并排站成一排,则不同的排法有
五个人并排站成一排,则不同的排法有
 种
种
 种
种
 种
种
 种
种
 一名老师和四名学生排成一排,老师不在两端,则不同的排法有
种.
一名老师和四名学生排成一排,老师不在两端,则不同的排法有
种.
 从
从 台甲型和
台甲型和 台乙型电视机中任取
台乙型电视机中任取 台,其中至少要甲、乙电视机各一台,则不同的取法有
种.
台,其中至少要甲、乙电视机各一台,则不同的取法有
种.
 把
把 个相同的小球放入编号为
个相同的小球放入编号为 的盒子中,问每个盒子中至少有
的盒子中,问每个盒子中至少有 个小球的不同放法有多少种?
个小球的不同放法有多少种?
 排列的概念:从
排列的概念:从 个不同元素中,任取
个不同元素中,任取 (
( )个元素(这里的被取元素各不相同)按照一定的顺序排成一列,叫做从
)个元素(这里的被取元素各不相同)按照一定的顺序排成一列,叫做从 个不同元素中取出
个不同元素中取出 个元素的一个排列
个元素的一个排列
 排列数的定义:从
排列数的定义:从 个不同元素中,任取
个不同元素中,任取 (
( )个元素的所有排列的个数叫做从
)个元素的所有排列的个数叫做从 个元素中取出
个元素中取出 元素的排列数,用符号
元素的排列数,用符号 表示
表示
 排列数公式:
排列数公式:
 (
( )
)
 阶乘:
阶乘: 表示正整数
表示正整数 到
到 的连乘积,叫做
的连乘积,叫做 的阶乘
的阶乘 规定
规定 .
.
 组合的概念:一般地,从
组合的概念:一般地,从 个不同元素中取出
个不同元素中取出
 个元素并成一组,叫做从
个元素并成一组,叫做从 个不同元素中取出
个不同元素中取出 个元素的一个组合.
个元素的一个组合.
 组合数的概念:从
组合数的概念:从 个不同元素中取出
个不同元素中取出
 个元素的所有组合的个数,叫做从
个元素的所有组合的个数,叫做从 个不同元素中取出
个不同元素中取出 个元素的组合数.用符号
个元素的组合数.用符号 表示.
表示.
 组合数公式:
组合数公式:

 .
.
 组合数的性质:
组合数的性质:
 .规定:
.规定: ;
; 
 =
= +
+
 附有限制条件的排列:
附有限制条件的排列:
①优先特殊元素(或位置)②相邻问题:“捆绑法””③不相邻问题:“插空法
④复杂问题:“排除法”⑤机会均等法;
 组合问题常见解题方法:
组合问题常见解题方法:
 注意“至少”、“最多”、“含”等词
注意“至少”、“最多”、“含”等词
 区分“分配”与“分组”:“分组问题”的特征是组与组之间只要元素个数相同是不可区分的,即指把物件分成组,是无顺序可言的;而“分配”问题即使元素个数相同,但因人不同,仍然是可区分的,或者是指把物件分给不同的人(或团体),是有顺序的,解分配问题必须先分组后排列,若平均分
区分“分配”与“分组”:“分组问题”的特征是组与组之间只要元素个数相同是不可区分的,即指把物件分成组,是无顺序可言的;而“分配”问题即使元素个数相同,但因人不同,仍然是可区分的,或者是指把物件分给不同的人(或团体),是有顺序的,解分配问题必须先分组后排列,若平均分 组,则分法
组,则分法 取法/
取法/
 隔板分组法:常常用于解决一类相同元素分给不同对象的分配问题.
隔板分组法:常常用于解决一类相同元素分给不同对象的分配问题.
 (
( 湖北文)把一同排
湖北文)把一同排 张座位编号为
张座位编号为 的电影票全部分给
的电影票全部分给 个人,每人至少分
个人,每人至少分 张,至多分
张,至多分 张,且这两张票具有连续的编号,那么不同的分法种数是
张,且这两张票具有连续的编号,那么不同的分法种数是








 (
( 天津)从集合
天津)从集合 中任选两个元素作为椭圆方程
中任选两个元素作为椭圆方程 中的
中的 、
、 ,
,
则能组成落在矩形区域 ,且
,且 内的椭圆个数为
内的椭圆个数为








 (
( 全国Ⅰ文)甲、乙、丙
全国Ⅰ文)甲、乙、丙 位同学选修课程,从
位同学选修课程,从 门课程中,甲选修
门课程中,甲选修 门,乙、丙各选修
门,乙、丙各选修 门,则不同的选修方案共有
门,则不同的选修方案共有 
 种
种 
 种
种 
 种
种 
 种
种
 (
( 全国Ⅱ文)
全国Ⅱ文) 位同学报名参加两个课外活动小组,每位同学限报其中的一个小组,则不同的报名方法共有
位同学报名参加两个课外活动小组,每位同学限报其中的一个小组,则不同的报名方法共有 
 种
种 
 种
种 
 种
种 
 种
种
 有一项活动,需在
有一项活动,需在 名老师、
名老师、 名男生和
名男生和 名女生中选人参加.
名女生中选人参加.
 若只需
若只需 人参加,有多少种不同的选法?
人参加,有多少种不同的选法?
 若需老师、男生、女生各
若需老师、男生、女生各 人参加,有多少种不同的选法?
人参加,有多少种不同的选法?
 若需
若需 名老师、
名老师、 名学生参加,有多少种不同的选法?
名学生参加,有多少种不同的选法?
 三边长均为正整数,且最大边长为
三边长均为正整数,且最大边长为 的三角形的个数为
的三角形的个数为







 若
若 是定义域为
是定义域为 ≤
≤ ≤
≤ ,
, ,值域为
,值域为 的函数,
的函数,
则这样的函数共有

 个
个 
 个
个 
 个
个 
 个
个


 名高中毕业生报考其中的
名高中毕业生报考其中的 所重点院校,每人只报一所院校,则有多少种不同的报名方法?
所重点院校,每人只报一所院校,则有多少种不同的报名方法?
 名高中毕业生报考其中的
名高中毕业生报考其中的 所重点院校,每人只报一所院校,每个院校仅允许报一名,有多少种不同的报名方法?
所重点院校,每人只报一所院校,每个院校仅允许报一名,有多少种不同的报名方法?
 从
从 ,…,
,…, 九个正整数中任取两个不同的数字分别作为对数和真数,共可以得到多少个不同的对数值?
九个正整数中任取两个不同的数字分别作为对数和真数,共可以得到多少个不同的对数值?
 从
从 中任取
中任取 个不同的数作为抛物线方程
个不同的数作为抛物线方程 (
( )
)
的系数,如果抛物线过原点,且顶点在第一象限,则这样的抛物线共有多少条?
 将
将 封信投入
封信投入 个邮筒,不同的投法共有
个邮筒,不同的投法共有

 种
种 
 种
种 
 种
种 
 种
种

 个学生在
个学生在 本不同的参考书中各挑选一本,不同选法种数是
本不同的参考书中各挑选一本,不同选法种数是








问题1. 在所有的两位数中,个位数字大于十位数字的两位数共有多少个?
在所有的两位数中,个位数字大于十位数字的两位数共有多少个?
 三人传球,由甲开始发球,并作第一次传球,经过
三人传球,由甲开始发球,并作第一次传球,经过 次传球后,球仍回到甲手中,则不同的传球方式共有
次传球后,球仍回到甲手中,则不同的传球方式共有 
 种
种 
 种
种 
 种
种 
 种
种
问题2. (
( 广州综合测试)某文艺团下基层进行宣传演出,原准备的节目表有
广州综合测试)某文艺团下基层进行宣传演出,原准备的节目表有
 个节目,如果保持这些节目的相对顺序不变,在它们之间再插入
个节目,如果保持这些节目的相对顺序不变,在它们之间再插入 个小品节目,并且这
个小品节目,并且这 个小品节目在节目表中既不排头,也不排尾,那么不同的插入方法有
个小品节目在节目表中既不排头,也不排尾,那么不同的插入方法有

 种
种

 种
种

 种
种

 种
种
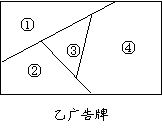
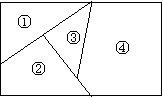
 用
用 种不同颜色为下列两块广告牌着色(如图),要求在①、②、③、④四个区域中相邻(有公共边界)的区域不用
种不同颜色为下列两块广告牌着色(如图),要求在①、②、③、④四个区域中相邻(有公共边界)的区域不用
同一种颜色.
(Ⅰ)若 ,为甲着色时
,为甲着色时
共有多少种不同等方法?
(Ⅱ)若为乙着色时共有
 种不同方法,求
种不同方法,求 .
.
 正整数
正整数 的正约数有 个.
的正约数有 个.
问题3.某外语组有 人,每人至少会英语和日语中的一门,其中
人,每人至少会英语和日语中的一门,其中 人会英语,
人会英语, 人会日语,从中选出会英语和日语的各一人,有多少种不同的选法?
人会日语,从中选出会英语和日语的各一人,有多少种不同的选法?
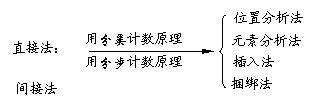
 分类计数原理(加法原理):做一件事情,完成它可以有
分类计数原理(加法原理):做一件事情,完成它可以有 类办法,在第一类办法中有
类办法,在第一类办法中有 种不同的方法,在第二类办法中有
种不同的方法,在第二类办法中有 种不同的方法,……,在第
种不同的方法,……,在第 类办法中有
类办法中有 种不同的方法
种不同的方法 那么完成这件事共有
那么完成这件事共有  种不同的方法.
种不同的方法.
 分步计数原理(乘法原理):
分步计数原理(乘法原理):
做一件事情,完成它需要分成 个步骤,做第一步有
个步骤,做第一步有 种不同的方法,做第二步有
种不同的方法,做第二步有 种不同的方法,……,做第
种不同的方法,……,做第 步有
步有 种不同的方法,那么完成这件事有:
种不同的方法,那么完成这件事有:
 种不同的方法.
种不同的方法.

 正确区分和使用两个原理是学好本章的关键.区分“分类与分步”的依据在于能否“一次性”完成. 若能“一次性”完成,则不需“分步”,只需分类;否则就分步处理.
正确区分和使用两个原理是学好本章的关键.区分“分类与分步”的依据在于能否“一次性”完成. 若能“一次性”完成,则不需“分步”,只需分类;否则就分步处理. 有些较复杂的问题,既要“分类”,又要“分步”,应明确按什么标准“分类”,“分步”,不同的标准,可以有不同的解法,解题时应择优而行.
有些较复杂的问题,既要“分类”,又要“分步”,应明确按什么标准“分类”,“分步”,不同的标准,可以有不同的解法,解题时应择优而行. 在应用计数原理时,要仔细审题,分清是允许重复,还是不允许重复.
在应用计数原理时,要仔细审题,分清是允许重复,还是不允许重复.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com