
 函数极限的定义:
函数极限的定义:
 当自变量
当自变量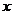 取正值并且无限增大时,如果函数
取正值并且无限增大时,如果函数 无限趋近于一个常数
无限趋近于一个常数 ,就说当
,就说当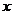 趋向于正无穷大时,函数
趋向于正无穷大时,函数 的极限是
的极限是 ,记作:
,记作: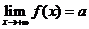 ,或者当
,或者当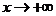 时,
时,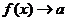 ;
;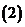 当自变量
当自变量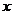 取负值并且绝对值无限增大时,如果函数
取负值并且绝对值无限增大时,如果函数 无限趋近于一个常数
无限趋近于一个常数 ,就说当
,就说当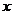 趋向于负无穷大时,函数
趋向于负无穷大时,函数 的极限是
的极限是 .
.
记作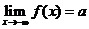 或者当当
或者当当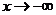 时,
时,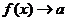
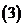 如果
如果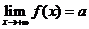 且
且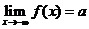 ,那么就说当
,那么就说当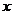 趋向于无穷大时,函数
趋向于无穷大时,函数 的极限是
的极限是 ,记作:
,记作: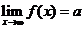 或者当
或者当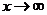 时,
时,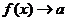 .
.
 常数函数:
常数函数: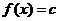 (
(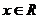 ),有
),有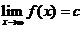 .
.
 存在,表示
存在,表示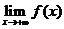 和
和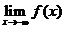 都存在,且两者相等
都存在,且两者相等 所以
所以 中的
中的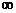 既有
既有 ,又有
,又有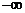 的意义,而数列极限
的意义,而数列极限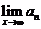 中的
中的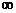 仅有
仅有 的意义.
的意义.
 趋向于定值的函数极限概念:当自变量
趋向于定值的函数极限概念:当自变量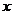 无限趋近于
无限趋近于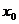 (
( )时,如果函数
)时,如果函数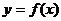 无限趋近于一个常数
无限趋近于一个常数 ,就说当
,就说当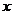 趋向
趋向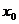 时,函数
时,函数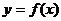 的极限是
的极限是 ,记作
,记作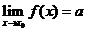 .特别地,
.特别地,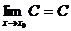 ;
;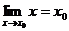 .
.
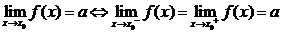 .
.
其中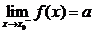 表示当
表示当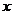 从左侧趋近于
从左侧趋近于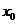 时的左极限,
时的左极限,
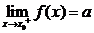 表示当
表示当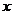 从右侧趋近于
从右侧趋近于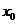 时的右极限.
时的右极限.
 对于函数极限有如下的运算法则:
对于函数极限有如下的运算法则:
如果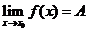 ,
,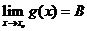 ,那么
,那么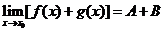 ,
,
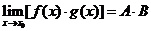 ,
, 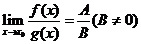 .
.
当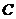 是常数,
是常数,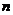 是正整数时:
是正整数时: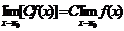 ,
,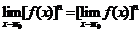
这些法则对于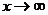 的情况仍然适用.
的情况仍然适用.
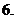 函数在一点连续的定义: 如果函数
函数在一点连续的定义: 如果函数 在点
在点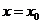 处有定义,
处有定义,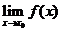 存在,
存在,
且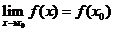 ,那么函数
,那么函数 在点
在点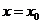 处连续.
处连续.
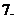 函数
函数 在
在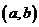 内连续的定义:如果函数
内连续的定义:如果函数 在某一开区间
在某一开区间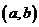 内每一点处连续,就说函数
内每一点处连续,就说函数 在开区间
在开区间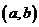 内连续,或
内连续,或 是开区间
是开区间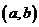 内的连续函数.
内的连续函数.
 函数
函数 在
在 上连续的定义:如果
上连续的定义:如果 在开区间
在开区间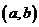 内连续,在左端点
内连续,在左端点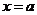 处有
处有 ,在右端点
,在右端点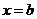 处有
处有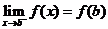 就说函数
就说函数 在闭区间
在闭区间 上连续,或
上连续,或 是闭区间
是闭区间 上的连续函数.
上的连续函数.
 最大值:
最大值: 是闭区间
是闭区间 上的连续函数,如果对于任意
上的连续函数,如果对于任意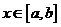 ,
,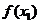 ≥
≥ ,那么
,那么 在点
在点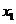 处有最大值
处有最大值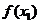 .
.
 最小值:
最小值: 是闭区间
是闭区间 上的连续函数,如果对于任意
上的连续函数,如果对于任意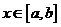 ,
,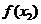 ≤
≤ ,那么
,那么 在点
在点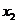 处有最小值
处有最小值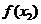 .
.
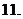 最大值最小值定理
最大值最小值定理
如果 是闭区间
是闭区间 上的连续函数,那么
上的连续函数,那么 在闭区间
在闭区间 上有最大值和最小值.
上有最大值和最小值.
 极限问题的基本类型:分式型,主要看分子和分母的首项系数;
极限问题的基本类型:分式型,主要看分子和分母的首项系数;
指数型(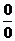 和
和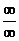 型),通过变形使得各式有极限;
型),通过变形使得各式有极限;
根式型(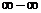 型),通过有理化变形使得各式有极限;
型),通过有理化变形使得各式有极限;
 根的存在定理:若①函数
根的存在定理:若①函数 在
在 上连续,②
上连续,②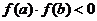 ,则方程
,则方程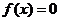 至少有一根在区间
至少有一根在区间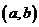 内;若①函数
内;若①函数 在
在 上连续且单调,②
上连续且单调,②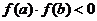 ,则方程
,则方程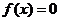 有且只有一根在区间
有且只有一根在区间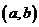 内.
内.
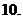 (
( 重庆)
重庆)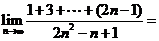
 (
(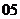 上海)计算:
上海)计算: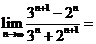
 (
(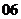 上海)计算:
上海)计算: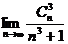 =
=
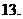 (
(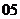 湖南)已知数列
湖南)已知数列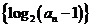 (
(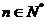 )为等差数列,且
)为等差数列,且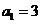 ,
, ,
,
则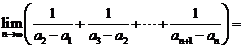
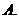

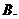
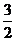
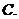
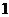
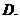
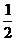
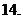 (
(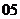 湖北)已知不等式
湖北)已知不等式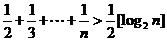 ,其中
,其中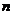 为大于
为大于 的整数,
的整数,
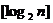 表示不超过
表示不超过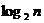 的最大整数. 设数列
的最大整数. 设数列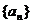 的各项为正,且满足
的各项为正,且满足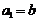
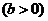 ,
,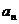 ≤
≤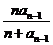 ,
,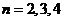 ,…
,…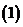 证明
证明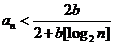 ,
,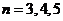 ,…
,…
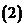 猜测数列
猜测数列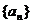 是否有极限?如果有,写出极限的值(不必证明);
是否有极限?如果有,写出极限的值(不必证明);
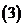 )试确定一个正整数
)试确定一个正整数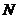 ,使得当
,使得当 时,对任意
时,对任意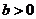 ,都有
,都有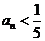 .
.
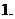 将
将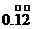 化成分数是
化成分数是
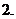 若
若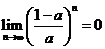 ,则
,则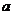 的取值范围是
的取值范围是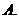
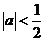
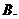
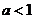
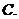
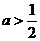
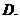
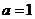
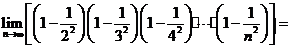
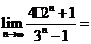 ;
;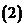
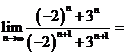
 已知
已知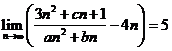 ,则
,则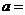 ;
;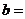 ;
;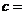
 (
( 湖北宜昌市
湖北宜昌市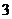 月模拟)已知数列
月模拟)已知数列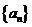 满足
满足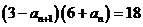 (
(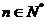 ),
),
且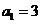 ,则
,则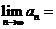
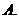

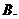
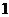
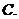
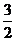
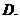
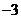
 (
(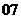 届高三湖北八校联考)已知数列
届高三湖北八校联考)已知数列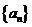 的前
的前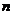 项和
项和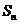 满足
满足 ,则其各项和
,则其各项和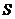 等于
等于
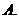
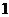
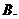
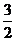
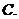
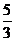
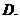
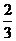
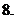 若数列
若数列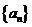 的通项公式是
的通项公式是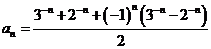 ,
,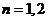 ,…,
,…,
则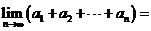
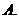
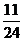
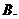

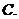

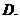
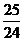
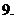 数列
数列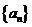 中,
中,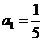 ,
,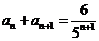 ,
,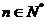 ,则
,则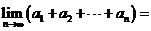
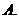
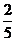
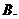
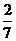
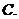
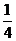
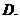
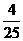
、
问题1.求下列数列的极限: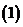
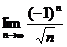 ;
; 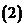
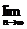
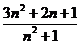 ;
; 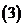
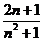
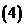

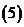
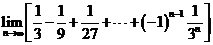
问题2.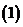 (
( 陕西)
陕西)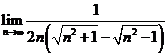 等于
等于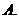
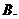
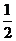
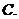
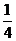
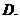

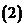 (
(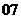 天津)设等差数列
天津)设等差数列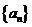 的公差
的公差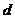 是
是 ,前
,前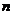 项的和为
项的和为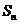 ,则
,则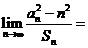
 (
(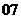 湖北)已知
湖北)已知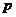 和
和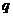 是两个不相等的正整数,且
是两个不相等的正整数,且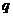 ≥
≥ ,则
,则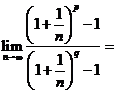
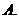

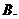
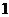
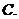
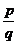
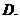
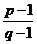
问题3.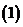 若
若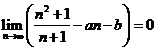 ,求
,求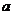 和
和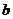 的值;
的值;
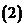 若
若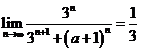 ,求
,求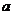 的取值范围.
的取值范围.
问题4.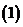 已知数列
已知数列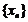 满足
满足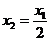 ,
, ,
,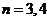 ,… ,
,… ,
若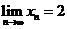 ,则
,则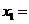
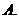
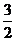
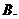
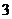
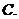
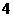
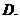
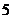
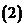 已知
已知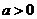 ,数列
,数列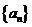 满足
满足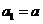 ,
,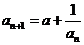 (
(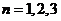 ,…),且数列
,…),且数列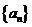 的极限存在,则
的极限存在,则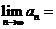 (结果用
(结果用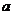 表示).
表示).
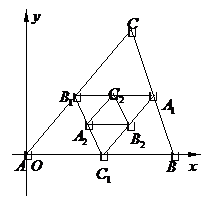 问题5.(
问题5.( 福建)如图,连结
福建)如图,连结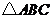 的各边中点
的各边中点
得到一个新的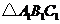 又连结
又连结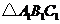 的各边中点得
的各边中点得
到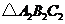 ,如此无限继续下去,得到一系列三角形:
,如此无限继续下去,得到一系列三角形:
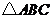 ,
,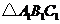 ,
,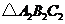 ,…,这一系列
,…,这一系列
三角形趋向于一个点 .已知
.已知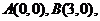
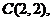
则点 的坐标是
的坐标是
 数列极限的定义:
数列极限的定义:
一般地,如果当项数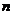 无限增大时,无穷数列
无限增大时,无穷数列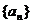 的项
的项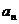 无限趋近于某个常数
无限趋近于某个常数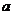
(即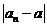 无限地接近于
无限地接近于 ),那么就说数列
),那么就说数列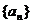 以
以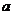 为极限.记作
为极限.记作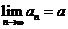 .
.
注: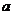 不一定是
不一定是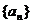 中的项
中的项
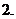 几个重要极限:
几个重要极限: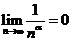 (
(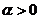 ,
,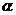 为常数);
为常数); 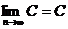 (
(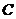 是常数);
是常数);
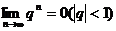 ;
;
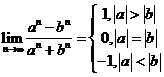
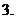 极限问题的基本类型:分式型,主要看分子和分母的首项系数;
极限问题的基本类型:分式型,主要看分子和分母的首项系数;
指数型(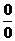 和
和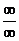 型),通过变形(如通分,约分)使得各式有极限;
型),通过变形(如通分,约分)使得各式有极限;
根式型(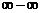 型),通过有理化变形使得各式有极限;
型),通过有理化变形使得各式有极限;
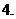 数列极限的运算法则:与函数极限的运算法则类似, 如果
数列极限的运算法则:与函数极限的运算法则类似, 如果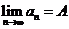 ,
,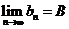 ,那么
,那么
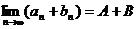
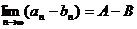
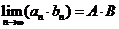
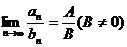 .
.
特别地,如果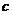 是常数,那么,
是常数,那么,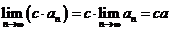
 无穷等比数列的各项和:
无穷等比数列的各项和: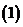 公比的绝对值小于
公比的绝对值小于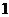 的无穷等比数列前
的无穷等比数列前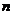 项的和当
项的和当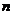 无限增大时的极限,叫做这个无穷等比数列各项的和,记做
无限增大时的极限,叫做这个无穷等比数列各项的和,记做 ;
;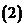
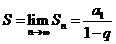
 (
( 上海)设
上海)设 是定义在正整数集上的函数,且
是定义在正整数集上的函数,且 满足:“当
满足:“当 成立时,总可推出
成立时,总可推出
 成立”.那么,下列命题总成立的是
成立”.那么,下列命题总成立的是
 若
若 成立,则当
成立,则当 时,均有
时,均有 成立
成立
 若
若 成立,则当
成立,则当 时,均有
时,均有 成立
成立
 若
若 成立,则当
成立,则当 时,均有
时,均有 成立
成立
 若
若 成立,则当
成立,则当 时,均有
时,均有 成立
成立
 (
( 湖南)已知函数
湖南)已知函数 ,数列{
,数列{ }满足:
}满足:
 ,
, ,
, 求证:
求证:
 ;
;
 .
.
 (
( 江西)已知数列
江西)已知数列 满足:
满足: ,且
,且 (
( ≥
≥ ,
, )
)
 求数列
求数列 的通项公式;
的通项公式; 求证:对于一切正整数
求证:对于一切正整数 ,不等式
,不等式
 (
( 湖北)已知
湖北)已知 为正整数,
为正整数,
 用数学归纳法证明:当
用数学归纳法证明:当 时,
时, ≥
≥ ;
;
 对于
对于 ≥
≥ ,已知
,已知 ,求证
,求证 ,
, ;
;
 求出满足等式
求出满足等式 的所有正整数
的所有正整数 .
.
 观察下列式子:
观察下列式子: ,则可以猜想的结论为:
,则可以猜想的结论为:
 用数学归纳法证明“
用数学归纳法证明“ ”,从“
”,从“ 到
到 ”左端需增乘的代数式为
”左端需增乘的代数式为








 (
( 重庆市重点中学二联)
重庆市重点中学二联) 如图,第
如图,第 个图形是由正
个图形是由正 边形“扩展”而来(
边形“扩展”而来( ,
, ,
, ,…),则第
,…),则第 个图形中共有
个顶点.
个图形中共有
个顶点.

 凸
凸 边形有
边形有 条对角线,则凸
条对角线,则凸 边形有对角线条数
边形有对角线条数 为
为








 平面内有
平面内有 条直线,其中任何两条不平行,任何三条不共点,求证:这
条直线,其中任何两条不平行,任何三条不共点,求证:这 条直线把平面分成
条直线把平面分成 个区域.
个区域.
问题1.求证: 能被
能被 整除.
整除.
问题2. 求证:
求证:
 设
设 ,且
,且 ,用数学归纳法证明:
,用数学归纳法证明:
 用数学归纳法证明:
用数学归纳法证明: (其中
(其中 ≥
≥ ,且
,且 ).
).
问题3.已知 ,
, ,其中
,其中 、
、 ,
, ,
, ,
, ,且
,且 .
. 求
求 的反函数
的反函数 ;
; 对任意
对任意 ,试指出
,试指出 与
与 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
问题4.( 浙江)设点
浙江)设点 ,
, 和抛物线
和抛物线 :
: (
( ),其中
),其中 =
= ,
, 由以下方法得到:
由以下方法得到: ,点
,点 在抛物线
在抛物线 :
: 上,点
上,点 到
到 的距离是
的距离是 到
到 上点的最短距离,…,点
上点的最短距离,…,点 在抛物线
在抛物线 :
: 上,点
上,点 到
到 的距离是
的距离是 到
到 上点的最短距离.
上点的最短距离.  求
求 及
及 的方程;
的方程; 证明
证明 是等差数列.
是等差数列.
 归纳法:由一些特殊事例推出一般结论的推理方法
归纳法:由一些特殊事例推出一般结论的推理方法 特点:特殊→一般.
特点:特殊→一般.
 不完全归纳法: 根据事物的部分(而不是全部)特例得出一般结论的推理方法叫做不完全归纳法
不完全归纳法: 根据事物的部分(而不是全部)特例得出一般结论的推理方法叫做不完全归纳法
 完全归纳法: 把研究对象一一都考查到了而推出结论的归纳法称为完全归纳法
完全归纳法: 把研究对象一一都考查到了而推出结论的归纳法称为完全归纳法
完全归纳法是一种在研究了事物的所有(有限种)特殊情况后得出一般结论的推理方法,又叫做枚举法.与不完全归纳法不同,用完全归纳法得出的结论是可靠的 通常在事物包括的特殊情况数不多时,采用完全归纳法
通常在事物包括的特殊情况数不多时,采用完全归纳法
 数学归纳法:对于某些与自然数
数学归纳法:对于某些与自然数 有关的命题常常采用下面的方法来证明它的正确性:先证明当
有关的命题常常采用下面的方法来证明它的正确性:先证明当 取第一个值
取第一个值 时命题成立;然后假设当
时命题成立;然后假设当 (
( ,
, ≥
≥ )时命题成立,证明当
)时命题成立,证明当 命题也成立
命题也成立 这种证明方法就叫做数学归纳法.
这种证明方法就叫做数学归纳法.
 数学归纳法的基本思想:即先验证使结论有意义的最小的正整数
数学归纳法的基本思想:即先验证使结论有意义的最小的正整数 ,如果当
,如果当 时,命题成立,再假设当
时,命题成立,再假设当 (
( ,
, ≥
≥ )时,命题成立.(这时命题是否成立不是确定的),根据这个假设,如能推出当
)时,命题成立.(这时命题是否成立不是确定的),根据这个假设,如能推出当 时,命题也成立,那么就可以递推出对所有不小于
时,命题也成立,那么就可以递推出对所有不小于 的正整数
的正整数 ,
, ,…,命题都成立.
,…,命题都成立.
 用数学归纳法证明一个与正整数有关的命题的步骤:
用数学归纳法证明一个与正整数有关的命题的步骤:
 证明:当
证明:当 取第一个值
取第一个值 结论正确;
结论正确; 假设当
假设当 (
( ,
, ≥
≥ )时结论正确,证明当
)时结论正确,证明当 时结论也正确
时结论也正确 由
由 ,
, 可知,命题对于从
可知,命题对于从 开始的所有正整数
开始的所有正整数 都正确.数学归纳法被用来证明与自然数有关的命题:递推基础不可少,归纳假设要用到,结论写明莫忘掉.
都正确.数学归纳法被用来证明与自然数有关的命题:递推基础不可少,归纳假设要用到,结论写明莫忘掉.

 用数学归纳法证题时,两步缺一不可;
用数学归纳法证题时,两步缺一不可; 证题时要注意两凑:一凑归纳假设,二凑目标.
证题时要注意两凑:一凑归纳假设,二凑目标.
 (
( 四川)甲校有
四川)甲校有 名学生,乙校有
名学生,乙校有 名学生,丙校有
名学生,丙校有 名学生,为统计三校学生某方面的情况,计划采用分层抽样法,抽取一个样本容量为
名学生,为统计三校学生某方面的情况,计划采用分层抽样法,抽取一个样本容量为 人的样本,应在这三校分别抽取学生
人的样本,应在这三校分别抽取学生

 人,
人, 人,
人, 人
人 
 人,
人, 人,
人, 人
人

 人,
人, 人,
人, 人
人 
 人,
人, 人,
人, 人
人
 (
( 天津) 某工厂生产
天津) 某工厂生产 、
、 、
、 三种不同型号的产品,产品数量之比依次为
三种不同型号的产品,产品数量之比依次为 ,现用分层抽样方法抽出一个容量为
,现用分层抽样方法抽出一个容量为 的样本,样本中
的样本,样本中 种型号产品有
种型号产品有 件.那么此样本的容量
件.那么此样本的容量
 (
( 陕西文)某商场有四类食品,其中粮食类、植物油类、动物性食品类及果蔬类分别有
陕西文)某商场有四类食品,其中粮食类、植物油类、动物性食品类及果蔬类分别有 种、
种、 种、
种、 种、
种、 种,现从中抽取一个容量为
种,现从中抽取一个容量为 的样本进行食品安全检测。若采用分层抽样的方法抽取样本,则抽取的植物油类与果蔬类食品种数之和是( )
的样本进行食品安全检测。若采用分层抽样的方法抽取样本,则抽取的植物油类与果蔬类食品种数之和是( ) 







 (
( 全国Ⅰ文)从某自动包装机包装的食盐中,随机抽取
全国Ⅰ文)从某自动包装机包装的食盐中,随机抽取 袋,测得各袋的质量分别为(单位:
袋,测得各袋的质量分别为(单位: ):
):
|
492 |
496 |
494 |
495 |
498 |
497 |
501 |
502 |
504 |
496 |
|
497 |
503 |
506 |
508 |
507 |
492 |
496 |
500 |
501 |
499 |
根据频率分布估计总体分布的原理,该自动包装机包装的袋装食盐质量在 -
- 之间的概率约为
之间的概率约为
 (
( 湖北)某初级中学有学生
湖北)某初级中学有学生 人,其中一年级
人,其中一年级 人,二、三年级各
人,二、三年级各 人,现要利用抽样方法抽取
人,现要利用抽样方法抽取 人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为
人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为 ,
, ,…,
,…, ;使用系统抽样时,将学生统一随机编号
;使用系统抽样时,将学生统一随机编号 ,
, ,…,
,…, ,并将整个编号依次分为
,并将整个编号依次分为 段.如果抽得号码有下列四种情况:
段.如果抽得号码有下列四种情况:
① ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ;
;
② ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ;
;
③ ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ;
;
④ ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ;
;
关于上述样本的下列结论中,正确的是
 ②、③都不能为系统抽样
②、③都不能为系统抽样  ②、④都不能为分层抽样
②、④都不能为分层抽样
 ①、④都可能为系统抽样
①、④都可能为系统抽样  ①、③都可能为分层抽样
①、③都可能为分层抽样
 (
( 湖南)设随机变量
湖南)设随机变量 服从标准正态分布
服从标准正态分布 ,已知
,已知 ,
,
则








 (
( 福建)两封信随机投入
福建)两封信随机投入 三个空邮箱,则
三个空邮箱,则 邮箱的信件数
邮箱的信件数 的数学期望
的数学期望
 (
( 浙江)已知随机变量
浙江)已知随机变量 服从正态分布
服从正态分布 ,
,
 ,
,
则








 (
( 全国Ⅱ)在某项测量中,测量结果
全国Ⅱ)在某项测量中,测量结果 服从正态分布
服从正态分布
 .若
.若 在
在 内取值的概率为
内取值的概率为 ,则
,则 在
在 内取值的概率为
内取值的概率为
 (
( 届高三浙江嘉兴市二检)已知随机变量
届高三浙江嘉兴市二检)已知随机变量 ,若
,若 ,则
,则








 (
( 辽宁文)某公司在过去几年内使用某种型号的灯管
辽宁文)某公司在过去几年内使用某种型号的灯管 支,该公司对这些灯管的使用寿命(单位:小时)进行了统计,统计结果如下表所示:
支,该公司对这些灯管的使用寿命(单位:小时)进行了统计,统计结果如下表所示:
|
分组 |
[500,900) |
[900,1100) |
[1100,1300) |
[1300,1500) |
[1500,1700) |
[1700,1900) |
[1900, ) ) |
|
频数 |
 |
 |
 |
 |
 |
 |
 |
|
频率 |
|
|
|
|
|
|
|
 将各组的频率填入表中;
将各组的频率填入表中;
 根据上述统计结果,计算灯管使用寿命不足
根据上述统计结果,计算灯管使用寿命不足 小时的频率;
小时的频率;
 该公司某办公室新安装了这种型号的灯管
该公司某办公室新安装了这种型号的灯管 支,若将上述频率作为概率,试求至少有
支,若将上述频率作为概率,试求至少有 支灯管的使用寿命不足
支灯管的使用寿命不足 小时的概率.
小时的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com