
10. (上海虹口区08学年高三数学第一学期期末试卷18)(本题满分13分)第1小题6分,第2小题7分.
已知: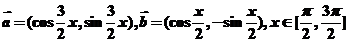 .
.
(1)求: 的取值范围;
的取值范围;
(2)求:函数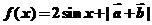 的最小值.
的最小值.
9.[解] :(1)f(x)= =−cos2x+
=−cos2x+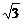 sinxcosx …………………2分
sinxcosx …………………2分
=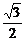 sin2x−
sin2x−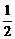 cos2x−
cos2x−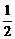 …………………………4分
…………………………4分
=sin(2x− )−
)−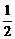 …………………………6分
…………………………6分
∵x∈[0,π],∴当x=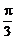 时,f(x)max=1−
时,f(x)max=1−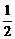 =
=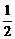 ………8分
………8分
(2)此时x=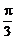 ,设向量
,设向量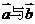 夹角为
夹角为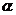 则cos
则cos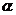 =
=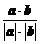 …………9分
…………9分
=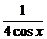 =
=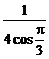 =
=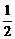 …………………………11分
…………………………11分
所以 向量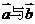 夹角为
夹角为 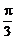 ………………12分
………………12分
9.(08年上海市部分重点中学高三联考17)(8+4)已知向量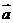 =(−cosx , sinx),
=(−cosx , sinx),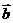 =(cosx ,
=(cosx ,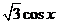 ),函数f(x)=
),函数f(x)=
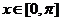
(1)求函数f(x)的最大值
(2)当函数f(x)取得最大值时,求向量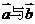 夹角的大小.
夹角的大小.
8.解:(1)设直角三角形两直角边长为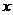 、
、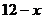 ,斜边长为
,斜边长为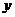 ,
,
则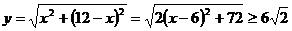
∴两直角边长为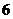 时,周长
时,周长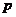 的最小值为
的最小值为 。
。
(2)设三角形中边长为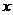 、
、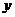 的两边所夹的角为
的两边所夹的角为 ,
,
则周长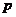

∴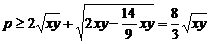 ,即
,即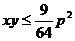
又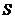
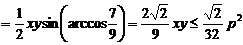 ,∴面积
,∴面积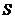 的最大值为
的最大值为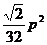 。
。
(3)不正确。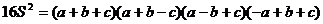
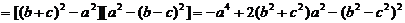

而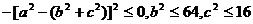 ,则
,则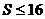 ,
,
其中等号成立的条件是 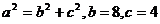 ,则
,则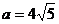
∴当三角形的边长为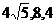 的直角三角形时,其面积取得最大值
的直角三角形时,其面积取得最大值 。
。
( 另法: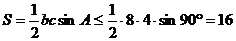 )
)
8.(上海市高考模拟试题22)(1)若直角三角形两直角边长之和为12,求其周长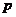 的最小值;
的最小值;
(2)若三角形有一个内角为 ,周长为定值
,周长为定值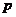 ,求面积
,求面积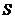 的最大值;
的最大值;
(3)为了研究边长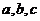 满足
满足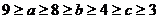 的三角形其面积是否存在最大值,现有解法如下:
的三角形其面积是否存在最大值,现有解法如下:
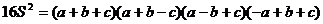
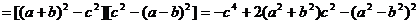
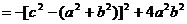
而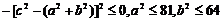 ,则
,则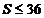 ,但是,其中等号成立的条件是
,但是,其中等号成立的条件是
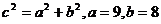 ,于是
,于是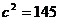 与
与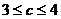 矛盾,
矛盾,
所以,此三角形的面积不存在最大值。
以上解答是否正确?若不正确,请你给出正确的答案。
(注: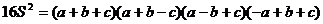 称为三角形面积的海伦公式,它已经被证明是正确的)
称为三角形面积的海伦公式,它已经被证明是正确的)
7.(本题满分12分)
设△ABC的内角∠A、∠B、∠C所对的边长分别为a、b、c,且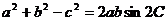 ,求角C的取值范围。
,求角C的取值范围。
解:由余弦定理,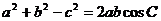 , …………2分
, …………2分
代入上式,得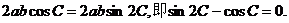 …………5分
…………5分
因为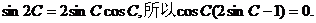 …………8分
…………8分
所以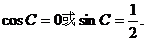 …………9分
…………9分
因为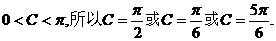 …………12分
…………12分
7.(上海市2009届高三年级十四校联考数学理科卷17)(本题满分12分)
设△ABC的内角∠A、∠B、∠C所对的边长分别为a、b、c,且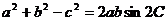 ,求角C的大小。
,求角C的大小。
6.解:由余弦定理,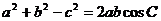 , …………2分
, …………2分
代入上式,得 …………4分
…………4分
因为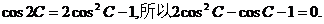 …………8分
…………8分
即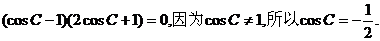 …………10分
…………10分
因为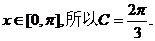 …………12分
…………12分
6.(上海市2009届高三年级十四校联考数学文科卷17)(本题满分12分)
设△ABC的内角∠A、∠B、∠C所对的边长分别为a、b、c,且 ,求角C的取值范围。
,求角C的取值范围。
5.解:(1)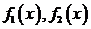 是“三角形函数”
是“三角形函数”
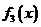 不是“三角形函数” ----1分
不是“三角形函数” ----1分
任给三角形,设它的三边长分别为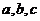 ,则
,则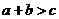 ,不妨假设
,不妨假设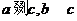 ,由于
,由于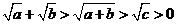 ,所以
,所以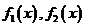 是“三角形函数”. -----------3分
是“三角形函数”. -----------3分
对于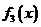 ,3,3,5可作为一个三角形的三边长,但
,3,3,5可作为一个三角形的三边长,但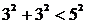 ,所以不存在三角形以
,所以不存在三角形以 为三边长,故
为三边长,故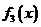 不是“三角形函数”.
------- ---- 4分
不是“三角形函数”.
------- ---- 4分
(2)设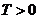 为
为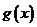 的一个周期,由于其值域为
的一个周期,由于其值域为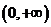 ,所以,存在
,所以,存在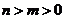 ,使得
,使得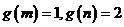 ,
,
取正整数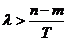 ,可知
,可知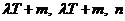 这三个数可作为一个三角形的三边长,但
这三个数可作为一个三角形的三边长,但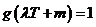 ,
,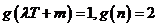 不能作为任何一个三角形的三边长.故
不能作为任何一个三角形的三边长.故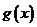 不是“三角形函数”.
-------------- -----10分
不是“三角形函数”.
-------------- -----10分
(3)(文)当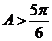 ,下证
,下证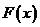 不是“三角形函数”.
不是“三角形函数”.
取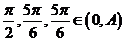 ,显然这三个数可作为一个三角形的三边长,但
,显然这三个数可作为一个三角形的三边长,但 不能作为任何一个三角形的三边长,
不能作为任何一个三角形的三边长,
故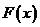 不是“三角形函数” --------18分
不是“三角形函数” --------18分
(3)(理)A的最大值为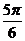 ------11分
------11分
一方面,若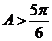 ,下证
,下证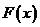 不是“三角形函数”.
不是“三角形函数”.
取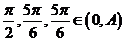 ,显然这三个数可作为一个三角形的三边长,但
,显然这三个数可作为一个三角形的三边长,但
 不能作为任何一个三角形的三边长,故
不能作为任何一个三角形的三边长,故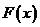 不是“三角形函数”. --------13分
不是“三角形函数”. --------13分
另一方面,以下证明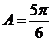 时,
时,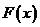 是“三角形函数”.
是“三角形函数”.
对任意三角形的三边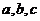 ,若
,若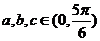 ,则分类讨论如下:
,则分类讨论如下:
(1)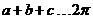 ,
,
此时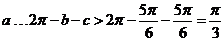 ,同理,
,同理, ,
,
∴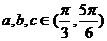 故
故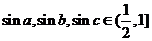 ,
,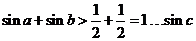 .
.
同理可证其余两式.
∴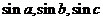 可作为某个三角形的三边长. -------15分
可作为某个三角形的三边长. -------15分
(2)
此时,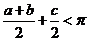 ,可得如下两种情况:
,可得如下两种情况:
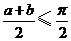 时,由于
时,由于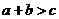 ,所以,
,所以,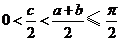 .
.
由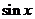 在
在 上的单调性可得
上的单调性可得 ;
;
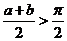 时,
时,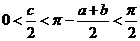 ,
,
同样,由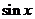 在
在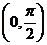 上的单调性可得
上的单调性可得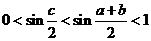 ;
;
总之, .
.
又由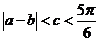 及余弦函数在
及余弦函数在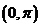 上单调递减,得
上单调递减,得
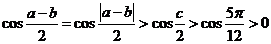 ,
,
∴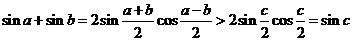 . -----17分
. -----17分
同理可证其余两式,所以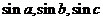 也是某个三角形的三边长.故
也是某个三角形的三边长.故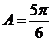 时,
时,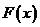 是“三角形函数”.
是“三角形函数”.
综上,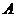 的最大值为
的最大值为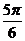 . --------18分
. --------18分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com