70.答案：

解析：.

69.答案：x

解法一：由f(x)在区间［0，1］上的图象为线段AB，可得：

f(x)＝－x+2，x∈［0，1］，因f(x)为偶函数，则任取x∈［－1，0］，－x∈［0，1］，f(x)＝f(－x)＝－(－x)+2＝x+2．

x∈［－1，0］，又f(x)是最小正周期为2的函数，若任取x∈［1，2］，则x－2∈［－1，0］，f(x)＝f(x－2)＝(x－2)+2＝x.x∈［1，2］，所以在区间［1，2］上，f(x)＝x.

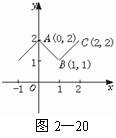
解法二：由函数f(x)是最小正周期为2的偶函数，它在区间［0，1］上的图象为线段AB，描出f(x)在区间［－1，0］和［1，2］上的图象如图2-20.可得f(x)在区间［1，2］上的图象为线段BC，其中B(1，1)，C(2，2)，所以在区间［1，2］上，f(x)＝x.

68.答案：1

解析：因为互为反函数的两函数图象关于直线y＝x对称，所以点Q′(2，5)必在

f(x)＝2^x+b的图象上，故有5＝2²+b，解得b＝1.

67.答案：(，3)

解析：由＞0，得＜0，利用根轴法如图2-19，得＜x＜3，所以函数定义域为(，3).

66.答案：1

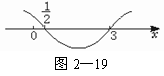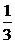解析：由，解得x=1，∴f^－1()=1.

64.答案：3

解析：当x∈(－∞，1，值域应为［，+∞)，当x∈(1，+∞)时值域应为(0，+∞)，

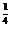∴y＝，y∈(0，+∞)，∴此时x∈(1，+∞)，∴log₈₁x＝，x＝81＝3

^※65.答案：如图2-18所示.

解析：由图中的沙化面积可以利用＝平均面积．因为题中是分了五六十年代、六七十年代、九十年代三段．

所以可分别求出三段的平均面积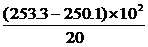＝16，

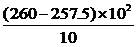＝21，＝25

63.答案：3

解析：f(x)=log₉x，log₉x，x=9=3.

62.答案：a+(b*c)=(a+b)*(a+c)

注：答案不惟一.

解析：∵a+(b*c)=a+，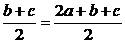

又(a+b)*(a+c)=.因此答案成立.

同时：(a*b)+c=(a*c)+(b*c)；a*(b+c)=(a+b)*c=(b+c)*a=(a+c)*b；(a*b)+c=(b*a)+c也符合题意.

评述：本题是一道开放型试题.属于“按新定义解题”题型，考查了考生活用知识以及思维敏捷性.这类题型正是今后高考数学命题的方向.

61.答案：x=2

解析：原方程可化为log₄(3x－1)=log₄［(x－1)(3+x)］，即3x－1=x²+2x+3(3x－1>0)，∴x²－x－2=0(3x－1>0)，解得x=2.

60.答案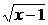：－(x≥1)

解析：∵f(x)=x²+1(x≤0)即y=x²+1，x²=y－1，∴x=－(y≥1)，∴f(x)的反函数为f^－1=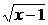－(x≥1).