
105.解:在定义域内任取x1<x2,
∴f(x1)-f(x2)=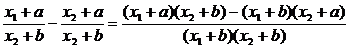
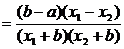 ,
,
∵a>b>0,∴b-a<0,x1-x2<0,
只有当x1<x2<-b或-b<x1<x2时函数才单调.
当x1<x2<-b或-b<x1<x2时f(x1)-f(x2)>0.
∴f(x)在(-b,+∞)上是单调减函数,在(-∞,-b)上是单调减函数.
评述:本小题主要考查了函数单调性的基本知识.
※106.解:(1)f(0)=1表示没有用水洗时,蔬菜上的农药量将保持原样.
(2)函数f(x)应该满足的条件和具有的性质是:f(0)=1,f(1)= ,
,
在[0,+∞)上f(x)单调递减,且0<f(x)≤1.
(3)设仅清洗一次,残留的农药量为f1=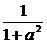 ,清洗两次后,残留的农药量为
,清洗两次后,残留的农药量为
f2=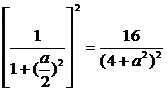 ,
,
则f1-f2=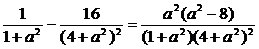 .
.
于是,当a>2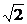 时,f1>f2;当a=2
时,f1>f2;当a=2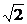 时,f1=f2;当0<a<2
时,f1=f2;当0<a<2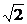 时,f1<f2.
时,f1<f2.
因此,当a>2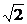 时,清洗两次后残留的农药量较少;
时,清洗两次后残留的农药量较少;
当a=2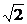 时,两种清洗方法具有相同的效果;
时,两种清洗方法具有相同的效果;
当0<a<2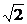 时,一次清洗残留的农药量较少.
时,一次清洗残留的农药量较少.
评述:本题主要考查运用所学数学知识和方法解决实际问题的能力.以及函数概念、性质和不等式证明的基本方法.
103.解:(1)∵x1,x2∈[0, ]都有f(x1+x2)=f(x1)·f(x2),
]都有f(x1+x2)=f(x1)·f(x2),
∴f(x)=f(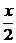 )f(
)f(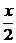 )≥0,x∈[0,1]
)≥0,x∈[0,1]
f(1)=f( +
+ )=f(
)=f( )·f(
)·f( )=[f(
)=[f( )]2
)]2
f( )=f(
)=f( +
+ )=f(
)=f( )·f(
)·f( )=[f(
)=[f( )]2,f(1)=a>0,
)]2,f(1)=a>0,
∴ .
.
(2)同上题(2)
(3)∵x∈[0, ]满足f(x1+x2)=f(x1)f(x2),I=2n(n∈Z)
]满足f(x1+x2)=f(x1)f(x2),I=2n(n∈Z)
∴f(x1+2n+x2+2n)=f(x1+2n)·f(x2+2n),
∵x1,x2在[2n, +2n]中也满足f(x1+x2)=f(x1)·f(x2)
+2n]中也满足f(x1+x2)=f(x1)·f(x2)
又∵f(1)=f(1)·f(0),∴f(0)=1,∴f(2n)=1
又∵f(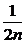 )=f2(
)=f2(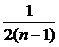 ),又∵f(
),又∵f( )=a
)=a ,∴f(
,∴f(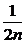 )=a
)=a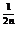
∴an=f(2n)f(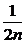 )=a
)=a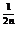 ,∴
,∴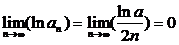
评述:本题考查函数的概念、图象,函数奇偶性和周期性以及数列极限等基础知识.设计循序渐进,依托基本的函数,进行一定的抽象并附加了一些条件,得到了一个既抽象又有一定具体背景的周期函数,这种抽象考查了对函数概念、函数性质的认识程度,特别是运用函数已知的图形的几何特征进一步剖析,挖掘函数未知的性质。在本题的设计中,以中学函数的基本概念为出发点,问题的提升与深入自然、明确.从函数基本知识,基本技能的考查延伸到数列极限的考查衔接紧密合理自然.体现了综合性试题的多方面的要求.
※104.解:设画面高为x cm,宽为λx cm,则λx2=4840.
设纸张面积为S,有S=(x+16)(λx+10)=λx2+(16λ+10)x+160,
将x=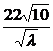 代入上式,得S=5000+44
代入上式,得S=5000+44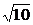 (8
(8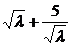 ).
).
当8 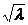 =
= ,即λ=
,即λ=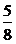 (
(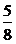 <1
<1 时,S取得最小值,
时,S取得最小值,
此时,高:x=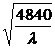 =88 cm,宽:λx=
=88 cm,宽:λx=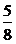 ×88=55 cm.
×88=55 cm.
答:画面高为88 cm,宽为55 cm时,能使所用纸张面积最小.
评述:本题主要考查建立函数关系式、求函数的最小值的方法和运用数学知识解决实际问题的能力.
102.(1)解:由f(x1+x2)=f(x1)·f(x2),x1,x2∈[0, ]知
]知
f(x)=f(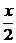 )·f(
)·f(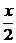 )≥0,x∈[0,1],∵f(1)=f(
)≥0,x∈[0,1],∵f(1)=f( +
+ )=f(
)=f( )·f(
)·f( )=
)=
[f( )]2,f(1)=2,∴f(
)]2,f(1)=2,∴f( )=2
)=2 .
.
∵f( )=f(
)=f( +
+ )=f(
)=f( )·f(
)·f( )=[f(
)=[f( )]2,f(
)]2,f( )=2
)=2 ,
,
∴f( )=2
)=2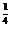 .
.
(2)证明:依题设y=f(x)关于直线x=1对称,
∴f(x)=(1+1-x),f(x)=f(2-x)
又∵f(-x)=f(x),∴f(-x)=f(2-x),∴f(x)=f(2+x),
∴f(x)是R上的周期函数,且2是它的一个周期.
101.(1)证明:根据题设,对任意x∈R,都有f(x)≤1.又f(x)=-b(x-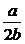 )2+
)2+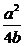 .∴f(
.∴f(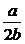 )=
)=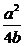 ≤1,∵a>0,b>0,∴a≤2
≤1,∵a>0,b>0,∴a≤2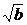 .
.
(2)证明:必要性:对任意x∈[0,1],|f(x)|≤1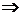 f(x)≥-1.据此可推出
f(x)≥-1.据此可推出
f(1)≥-1,即a-b≥-1,∴a≥b-1.
对任意x∈[0,1],|f(x)|≤1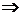 f(x)≤1,因为b>1,可得0<
f(x)≤1,因为b>1,可得0<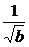 <1,可推出f(
<1,可推出f(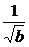 )≤1,即a·
)≤1,即a·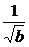 -1≤1,∴a≤2
-1≤1,∴a≤2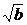 ,∴b-1≤a≤2
,∴b-1≤a≤2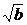 .
.
充分性:因为b>1,a≥b-1,对任意x∈[0,1],可以推出ax-bx2≥b(x-x2)-x≥-x≥-1,即ax-bx2≥-1,因为b>1,a≤2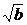 ,对任意x∈[0,1],可以推出:
,对任意x∈[0,1],可以推出:
ax-bx2≤2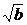 x-bx2-b(x-
x-bx2-b(x-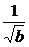 )2+1≤1,即ax-bx2≤1,∴-1≤f(x)≤1.
)2+1≤1,即ax-bx2≤1,∴-1≤f(x)≤1.
综上,当b>1时,对任意x∈[0,1],|f(x)|≤1的充要条件是b-1≤a≤2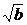 .
.
(3)解:因为a>0,0<b≤1时,对任意x∈[0,1]有f(x)=ax-bx2≥-b≥-1,即f(x)≥-1;
f(x)≤1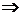 f(1)≤1
f(1)≤1 a-b≤1,即a≤b+1,又a≤b+1
a-b≤1,即a≤b+1,又a≤b+1 f(x)≤(b+1)x-bx2≤1,即f(x)≤1.
f(x)≤(b+1)x-bx2≤1,即f(x)≤1.
所以,当a>0,0<b≤1时,对任意x∈[0,1],|f(x)|≤1的充要条件是a≤b+1.
评述:本题主要考查二次函数、不等式、充要条件的综合运用,考查分类讨论思想和逻辑推理能力以及思维能力.
100.解:(1)当θ=-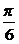 时
时
f(x)=x2-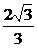 x-1=(x-
x-1=(x-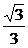 )2-
)2-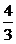 ,x∈[-1,
,x∈[-1,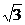 ]
]
∴x=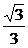 时,f(x)的最小值为-
时,f(x)的最小值为-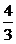
x=-1时,f(x)的最大值为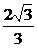
(2)函数f(x)=(x+tanθ)2-1-tan2θ图象的对称轴为x=-tanθ
∵y=f(x)在区间[-1,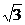 ]上是单调函数
]上是单调函数
∴-tanθ≤-1或-tanθ≥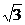
即tanθ≥1或tanθ≤-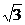
因此,θ的取值范围是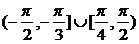
99.解:(1)当a=-1时,f(x)=x2-2x+2=(x-1)2+1,x∈[-5,5]
∴x=1时,f(x)的最小值为1
x=-5时,f(x)的最大值为37
(2)函数f(x)=(x+a)2+2-a2图象的对称轴为x=-a
∵f(x)在区间[-5,5]上是单调函数
∴-a≤-5或-a≥5
故a的取值范围是a≤-5或a≥5.
98.解:(1)、(2)同上题
(3)解法一:由f(a2)=af(a)+af(a)=2af(a)
f(a3)=a2f(a)+af(a2)=3a2f(a)
猜测f(an)=nan-1f(a).
下面用数学归纳法证明:
①当n=1时,f(a1)=1·a0·f(a),公式成立;
②假设当n=k时,f(ak)=kak-1f(a)成立,
那么当n=k+1时
f(ak+1)=akf(a)+af(ak)=akf(a)+kakf(a)=(k+1)akf(a),公式仍成立.
由上两步可知,对任意n∈N,f(an)=nan-1f(a)成立.
所以
因为f(2)=2,f(1)=f(2· )=2f(
)=2f( )+
)+ f(2)=0
f(2)=0
所以f( )=-
)=- f(2)=-
f(2)=-
un=(- )·(
)·( )n-1(n∈N)
)n-1(n∈N)
因此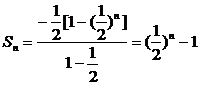 (n∈N)
(n∈N)
解法二:当ab≠0时,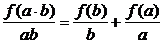
令g(x)=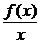 ,则g(a·b)=g(a)+g(b)
,则g(a·b)=g(a)+g(b)
故g(an)=ng(a)
所以f(an)=an·g(an)=nang(a)=nan-1f(a)
所以un=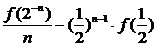
(以下同解法一)
评述:这是一个研究抽象函数的问题,学生应该在第(1)问的基础上,利用奇偶函数的定义,计算f(-x)是此题的切入点.第(3)问应该在归纳假设的基础上,充分利用所给函数的关系式.
97.(1)解:f(0)=f(0·0)=0·f(0)+0·f(0)=0
由f(1)=f(1·1)=1·f(1)+1·f(1),
得f(1)=0.
(2)f(x)是奇函数
证明:因为f(1)=f[(-1)2]=-f(-1)-f(-1)=0
所以f(-1)=0
f(-x)=f(-1·x)=-f(x)+xf(-1)=-f(x).
因此,f(x)为奇函数
(3)证明:先用数学归纳法证明un=f(2n)>0(n∈N)
①当n=1时,u1=f(2)=2>0;
②假设当n=k时,uk=f(2k)>0
那么当n=k+1时,uk+1=f(2k+1)=2f(2k)+2kf(2)=2f(2k)+2k+1>0.
由以上两步可知,对任意n∈N,un=f(2n)>0.
因为un>0(n∈N)
所以un+1=f(2n+1)=2f(2n)+2nf(2)=2un+2n+1>un(n∈N)
96.解:(1)当a=0时,函数f(-x)=(-x)2+|-x|+1=f(x),此时f(x)为偶函数.
当a≠0时,f(a)=a2+1,f(-a)=a2+2|a|+1,f(-a)≠f(a),f(-a)≠-f(a).
此时函数f(x)既不是奇函数,也不是偶函数
(2)①当x≤a时,函数f(x)=x2-x+a+1=(x- )2+a+
)2+a+ .
.
若a≤ ,则函数f(x)在(-∞,a]上单调递减,从而,函数f(x)在(-∞,a]上的最小值为f(a)=a2+1.
,则函数f(x)在(-∞,a]上单调递减,从而,函数f(x)在(-∞,a]上的最小值为f(a)=a2+1.
若a> ,则函数f(x)在(-∞,a
,则函数f(x)在(-∞,a 上的最小值为f(
上的最小值为f( )=
)= +a,且f(
+a,且f( )≤
)≤
f(a).
②当x≥a时,函数f(x)=x2+x-a+1=(x+ )2-a+
)2-a+ .
.
若a≤- ,则函数f(x)在[a,+∞
,则函数f(x)在[a,+∞ 上的最小值为f(-
上的最小值为f(- )=
)= -a,且f(-
-a,且f(- )≤f(a).
)≤f(a).
若a>- ,则函数f(x)在[a,+∞)上单调递增,从而,函数f(x)在[a,+∞)上的最小值为f(a)=a2+1.
,则函数f(x)在[a,+∞)上单调递增,从而,函数f(x)在[a,+∞)上的最小值为f(a)=a2+1.
综上,当a≤- 时,函数f(x)的最小值是
时,函数f(x)的最小值是 -a.
-a.
当- <a≤
<a≤ 时,函数f(x)的最小值是a2+1.
时,函数f(x)的最小值是a2+1.
当a> 时,函数f(x)的最小值是a+
时,函数f(x)的最小值是a+ .
.
评述:函数奇偶性的讨论问题是中学数学的基本问题,如果平时注意知识的积累,对解此题会有较大帮助.因为x∈R,f(0)=|a|+1≠0,由此排除f(x)是奇函数的可能性.运用偶函数的定义分析可知,当a=0时,f(x)是偶函数,第2题主要考查学生的分类讨论思想、对称思想.
95.解:(1)f(2)=3,f(-2)=7
由于f(-2)≠f(2),f(-2)≠-f(2)
故f(x)既不是奇函数,也不是偶函数
(2)f(x)=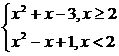
由于f(x)在[2,+∞)上的最小值为f(2)=3,在(-∞,2)内的最小值为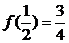 .
.
故函数f(x)在(-∞,+∞)内的最小值为 .
.
评述:因为奇偶函数问题要紧紧抓住“任取”“都有”这两个关键词.f(-x)与f(x)要同时有意义,f(x)与f(-x)要么相等,要么互为相反数,而要讨论非奇非偶只要说明不满足上述两点之一即可.另外,也可以借助分段函数的草图,帮助分析,然后用代数方法来回答.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com