
1.有关函数单调性和奇偶性的试题,从试题上看,抽象函数和具体函数都有,前些年大多数考具体函数,近几年都有在不给出具体函数的情况下求解问题的试题,可见有向抽象函数发展的趋势,另外试题注重对转化思想的考查,且都综合地考查单调性与奇偶性.
加强对函数单调性、奇偶性的应用训练也是复习的重点,也就是在已知函数已具有奇偶性或单调性的性质条件下,在解题中如何合理地运用这些性质解题.首先应熟练掌握二次函数、反比例函数、指数函数、对数函数,以及形如y=x+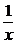 的函数等一些常见函数的性质,归纳提炼函数性质的应用规律.再如函数单调性的用法主要是逆用定义等.
的函数等一些常见函数的性质,归纳提炼函数性质的应用规律.再如函数单调性的用法主要是逆用定义等.
116.解:f(x1)+f(x2)=logax1+logax2=loga(x1·x2),∵x1,x2∈(0,+∞),
∴x1·x2≤( )2(当且仅当x1=x2时取“=”号)
)2(当且仅当x1=x2时取“=”号)
当a>1时,有logax1x2≤loga( )2.∴
)2.∴ loga(x1x2)≤loga
loga(x1x2)≤loga ,
, (logax1+logax2)≤loga
(logax1+logax2)≤loga ,即
,即 [f(x1)+f(x2)]≤f(
[f(x1)+f(x2)]≤f( )(当且仅当x1=x2时,取“=”号)
)(当且仅当x1=x2时,取“=”号)
当0<a<1时,有logax1·x2≥loga( )2,即
)2,即 [f(x1)+f(x2)]≥f(
[f(x1)+f(x2)]≥f( )(当且仅当x1=x2时,取“=”号).
)(当且仅当x1=x2时,取“=”号).
评述:本题考查了对数的基本性质、平均值不等式等知识.运用了分类讨论的思想,考查了推理论证的能力.
●命题趋向与应试策略
115.解:将方程变形得9·3x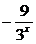 -80=0,
-80=0,
于是9·(3x)2-80·3x-9=0
分解因式得(3x-9)(9·3x+1)=0,
因为9·3x+1≠0,所以3x-9=0,x=2,
经检验x=2是原方程的解.
评述:本题主要考查指数方程的解法,属常规题.应用换元法,将方程转化成二次方程求解.
114.解:(1)由点A的坐标为(0,9)得c=9,即轨迹方程为y=ax2+9,令y=0,
得ax2+9=0,x2=-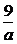 .
.
由题意,6<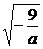 <7,解得:
<7,解得: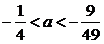 .
.
(2)若物体又经过点P(2,8.1),则8.1=4a+9,解得a=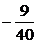 .
.
因为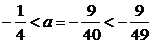 .所以物体能落在D内.
.所以物体能落在D内.
113.解:设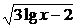 =y,原方程化为y-y2+2=0.
=y,原方程化为y-y2+2=0.
解得y=-1,y=2.
因为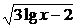 ≥0,所以将y=-1舍去.
≥0,所以将y=-1舍去.
由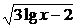 =2,得lgx=2,所以x=100.
=2,得lgx=2,所以x=100.
经检验,x=100为原方程的解.
评述:本题主要考查对数方程、无理方程的解法和运算能力.训练不规范,往往不验根造成失分.
112.解:(1)当a= 时,f(x)=x+
时,f(x)=x+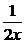 +2,
+2,
∵f(x)在区间[1,+∞)上为增函数,
∴f(x)在区间[1,+∞)上的最小值为f(1)=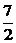 .
.
(2)方法一:在区间[1,+∞)上,f(x)= >0恒成立
>0恒成立
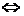 x2+2x+a>0恒成立.
x2+2x+a>0恒成立.
设y=x2+2x+a,x∈[1,+∞),
y=x2+2x+a=(x+1)2+a-1递增,∴当x=1时,ymin=3+a,
于是当且仅当ymin=3+a>0时,函数f(x)恒成立,故a>-3.
方法二:f(x)=x+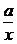 +2,x∈[1,+∞),
+2,x∈[1,+∞),
当a≥0时,函数f(x)的值恒为正,当a<0时,函数f(x)递增,
故当x=1时,f(x)min=3+a,于是当且仅当
f(x)min=3+a>0时,函数f(x)>0恒成立,故a>-3.
方法三:在区间[1,+∞ 上f(x)=
上f(x)= x恒成立
x恒成立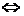 x2+2x+a>0恒成立?
x2+2x+a>0恒成立?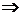 a>-x2-2x恒成立
a>-x2-2x恒成立
又∵x∈[1,+∞]a>-x2-2x恒成立
∴a应大于u=-x2-2x,x∈[1,+∞ 的最大值
的最大值
∴a>-(x+1)2+1,x=1时u取得最大值,∴a>-3
评述:本题主要考查函数与不等式性质及分类讨论的数学思想方法.
111.解:当x≤-1时,设f(x)=x+b,则由0=-2+b,即b=2,得f(x)=x+2;
当-1<x<1时,设f(x)=ax2+2,
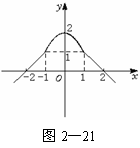
则由1=a(-1)2+2,即a=-1,得f(x)=-x2+2;
当x≥1时,f(x)=-x+2.
故f(x)=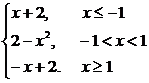
110.证明:方法一:由已知f(x)=|lgx|=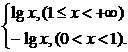
∵0<a<b,f(a)>f(b),∴a、b不能同时在区间[1,+∞)上,又由于0<a<b,故必有a∈(0,1);
若b∈(0,1),显然有ab<1.若b∈[1,+∞ ,由f(a)-f(b)>0,
,由f(a)-f(b)>0,
有-lga-lgb>0,故lgab<0,∴ab<1.
方法二:由题设f(a)>f(b),即|lga|>|lgb|,上式等价于(lga)2>(lgb)2
(lga+lgb)(lga-lgb)>0,lg(ab)lg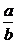 >0,由已知b>a>0,∴
>0,由已知b>a>0,∴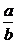 <1,
<1,
∴lg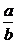 <0,∴lg(ab)<0,0<ab<1
<0,∴lg(ab)<0,0<ab<1
 评述:本小题主要考查函数的单调性、对数函数的性质、运算能力,考查分析解决问题的能力.
评述:本小题主要考查函数的单调性、对数函数的性质、运算能力,考查分析解决问题的能力.
109.解:原函数式可化成f(x)=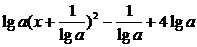 .
.
由已知,f(x)有最大值3,所以lga<0,并且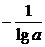 +4lga=3,
+4lga=3,
整理得 4(lga)2-3lga-1=0,解得 lga=1,lga=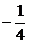 .
.
∵lga<0,故取lga=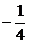 .∴a=
.∴a=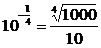 .
.
评述:本小题主要考查二次函数最大值和最小值的概念以及对于配方法、对数方程、二次方程的解法的运用能力.
107.解:(1)∵f(x)=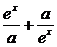 是R上的偶函数,∴f(x)-f(-x)=0.
是R上的偶函数,∴f(x)-f(-x)=0.
∴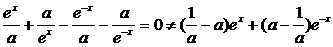
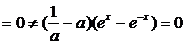
ex-e-x不可能恒为“0”,∴当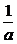 -a=0时等
-a=0时等
式恒成立,∴a=1.
(2)在(0,+∞)上任取x1<x2,
f(x1)-f(x2)=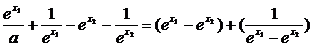
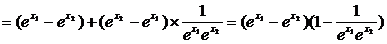
∵e>1,∴0< >1,∴
>1,∴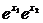 >1
>1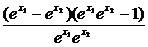 <0,
<0,
∴f(x1)-f(x2)<0,
∴f(x)是在[0,+∞)上的增函数.
评述:本题主要考查了函数的奇偶性以及单调性的基础知识.
※108.解:(1)由图(1)可得市场售价与时间的函数关系为
f(t)=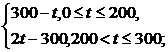
由图(2)可得种植成本与时间的函数关系为
g(t)=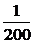 (t-150)2+100,0≤t≤300.
(t-150)2+100,0≤t≤300.
(2)设t时刻的纯收益为h(t),则由题意得h(t)=f(t)-g(t),
即h(t)=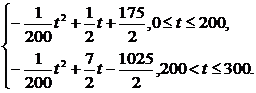
当0≤t≤200时,配方整理得h(t)=-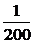 (t-50)2+100,
(t-50)2+100,
所以,当t=50时,h(t)取得区间[0,200]上的最大值100;
当200<t≤300时,配方整理得
h(t)=-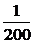 (t-350)2+100,
(t-350)2+100,
所以,当t=300时,h(t)取得区间(200,300]上的最大值87.5.
综上,由100>87.5可知,h(t)在区间[0,300]上可以取得最大值100,此时t=50,即从二月一日开始的第50天时,上市的西红柿纯收益最大.
评述:本题主要考查由函数图象建立函数关系式和求函数最大值的问题.考查运用所学知识解决实际问题的能力.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com