
2.
OA的垂直平分线方程为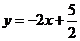 ,令
,令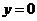 ,得
,得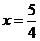 ,因此焦点
,因此焦点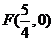 .
.
所以抛物线方程为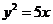 ,准线方程为
,准线方程为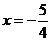 .
.
1.
设抛物线方程为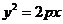 ,过
,过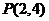 ,所以
,所以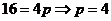 ,方程为
,方程为 .
.
5.
解:若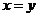 ,则
,则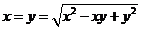 ,各角均为
,各角均为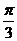 .
.
若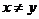 ,不妨设
,不妨设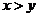 ,则有
,则有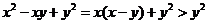 ,
,
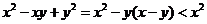 ,即
,即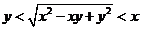 ,最长边为
,最长边为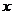 ,最短边为
,最短边为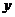 .
.
设夹角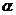 ,则有
,则有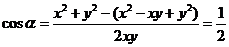 ,
,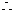
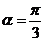 .
.
4.
解:设此直角三角形的两直角边的长分别为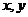 ,则斜边长为
,则斜边长为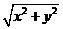 ,根据题意有
,根据题意有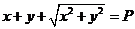 .
.

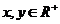 ,
,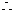
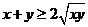 ,
,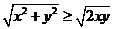 (当且仅当
(当且仅当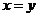 时取等号),
时取等号),
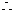
 ,即
,即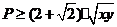 ,
,
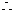
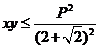 ,
,
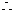 当
当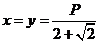 时,此三角形面积的最大值为
时,此三角形面积的最大值为 .
.
3.
解:令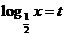 ,则
,则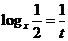 ,原不等式即为
,原不等式即为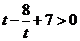 ,整理得
,整理得
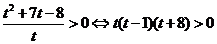 ,
,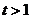 或
或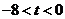 ,即
,即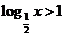 或
或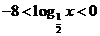 .
.
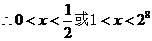 .
.
2.
解:原不等式
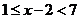 或
或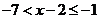 ,即
,即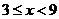 或
或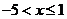 ,所以原不等式的解集为
,所以原不等式的解集为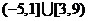 .
.
1.
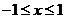 解析:
解析: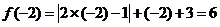 ,
,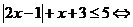
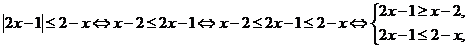
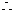
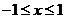 .
.
4.
A 解析: 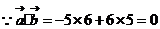 ,
,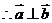 .
.
3. C 解析:
A.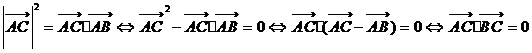
故A成立.
B.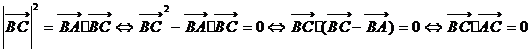 , 故B成立.
, 故B成立.
D. 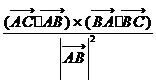
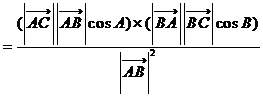
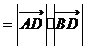
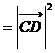
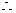 D成立,故选C.
D成立,故选C.
2.
B 解析:依题意可设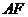 所在直线方程为
所在直线方程为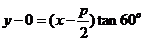 ,
,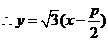 .
.
联立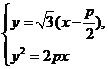 解得
解得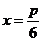 与
与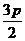 .
.
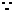
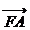 与
与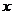 轴正向的夹角为
轴正向的夹角为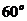 ,
,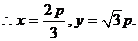
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com