
12.设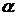 和
和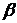 为不重合的两个平面,给出下列命题:
为不重合的两个平面,给出下列命题:
(1)若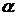 内的两条相交直线分别平行于
内的两条相交直线分别平行于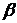 内的两条直线,则
内的两条直线,则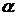 平行于
平行于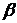 ;
;
(2)若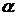 外一条直线
外一条直线 与
与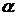 内的一条直线平行,则
内的一条直线平行,则 和
和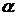 平行;
平行;
(3)设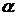 和
和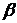 相交于直线
相交于直线 ,若
,若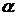 内有一条直线垂直于
内有一条直线垂直于 ,则
,则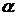 和
和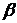 垂直;
垂直;
(4)直线 与
与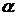 垂直的充分必要条件是
垂直的充分必要条件是 与
与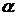 内的两条直线垂直.
内的两条直线垂直.
上面命题中,真命题的序号 ★ (写出所有真命题的序号).
[答案](1)(2)
[解析]略
11.已知集合 ,
,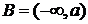 ,若
,若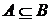 则实数
则实数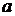 的取值范围是
的取值范围是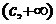 ,其中
,其中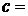 ★ .
★ .
[答案]4
[解析]由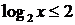 得
得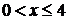 ,
,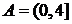 ;由
;由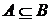 知
知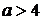 ,所以
,所以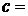 4。
4。
10.已知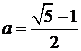 ,函数
,函数 ,若实数
,若实数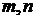 满足
满足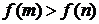 ,则
,则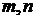 的大小关系为 ★ .
的大小关系为 ★ .
[答案]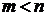
[解析]略
9.在平面直角坐标系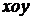 中,点P在曲线
中,点P在曲线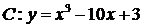 上,且在第二象限内,已知曲线C在点P处的切线的斜率为2,则点P的坐标为 ★ .
上,且在第二象限内,已知曲线C在点P处的切线的斜率为2,则点P的坐标为 ★ .
[答案]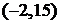 、
、
[解析]略
8.在平面上,若两个正三角形的边长的比为1:2,则它们的面积比为1:4,类似地,在空间,若两个正四面体的棱长的比为1:2,则它们的体积比为 ★ .
[答案]1:8
[解析]略
7.右图是一个算法的流程图,最后输出的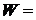 ★ .
★ .
[答案]22
[解析]略
6.某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如下表:
|
学生 |
1号 |
2号 |
3号 |
4号 |
5号 |
|
甲班 |
6 |
7 |
7 |
8 |
7 |
|
乙班 |
6 |
7 |
6 |
7 |
9 |
 则以上两组数据的方差中较小的一个为
则以上两组数据的方差中较小的一个为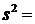 ★ .
★ .
[答案]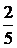
[解析]略
5.现有5根竹竿,它们的长度(单位:m)分别为2.5,2.6,2.7,2.8,2.9,若从中一次随机抽取2根竹竿,则它们的长度恰好相差0.3m的概率为 ★ .
[答案]0.2
[解析]略
4.函数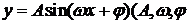 为常数,
为常数,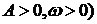 在闭区间
在闭区间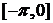 上的图象如图所示,则
上的图象如图所示,则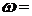 ★ .
★ .
[答案]3
[解析]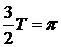 ,
,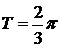 ,所以
,所以 ,
,
3.函数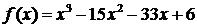 的单调减区间为 ★ .
的单调减区间为 ★ .
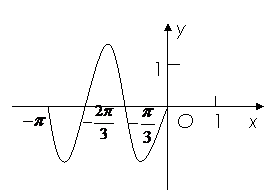 [答案]
[答案]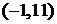
[解析]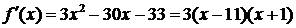 ,由
,由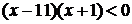 得单调减区间为
得单调减区间为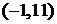 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com