
7、解:(1)∵ ,∴
,∴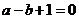 ,……………………(1分)
,……………………(1分)
又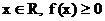 恒成立,∴
恒成立,∴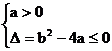 -………………(2分),
-………………(2分),
∴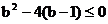 ,∴
,∴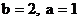 ………………(3分).
………………(3分).
∴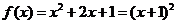 . ………………(4分)
. ………………(4分)
(2)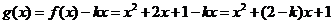 ………………(5分)
………………(5分)
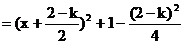 ,当
,当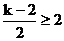 或
或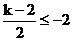 时,………(7分)
时,………(7分)
即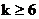 或
或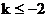 时,
时,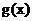 是单调函数.…………………………(8分)
是单调函数.…………………………(8分)
(3) ∵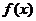 是偶函数,∴
是偶函数,∴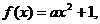 …………………………(9分)
…………………………(9分)
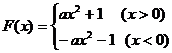 ………………………………(10分),
………………………………(10分),
∵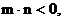 设
设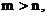 则
则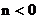 .又
.又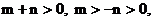
∴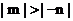 ,------(12分)
,------(12分)
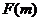 +
+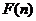
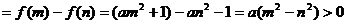 ,
,
∴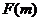 +
+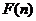 能大于零. …………………………(14分)
能大于零. …………………………(14分)
6、(Ⅰ)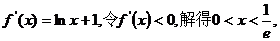
 ……2分
……2分

 ……4分
……4分
(Ⅱ)(ⅰ)0<t<t+2<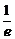 ,t无解;……5分
,t无解;……5分
(ⅱ)0<t<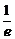 <t+2,即0<t<
<t+2,即0<t<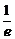 时,
时,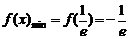 ;……7分
;……7分
(ⅲ)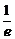
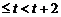 ,即
,即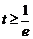 时,
时,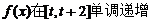 ,
,
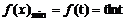 ……9分
……9分
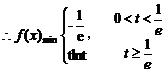 ……10分
……10分
(Ⅲ)由题意: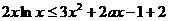 在
在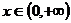 上恒成立
上恒成立
即 可得
可得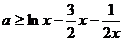 ……11分
……11分
设 , 则
, 则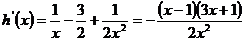 ……12分
……12分
令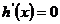 ,得
,得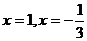 (舍)
(舍)
当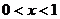 时,
时,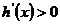 ;当
;当 时,
时, 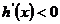
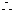 当
当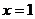 时,
时, 取得最大值,
取得最大值, 
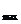 =-2……13分
=-2……13分
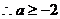 .
.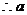 的取值范围是
的取值范围是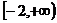 .……14分
.……14分
5、解:(Ⅰ)令 
令 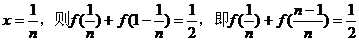 …………4分
…………4分
(Ⅱ)∵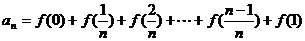 ①
①
∴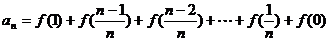 ②
②
由(Ⅰ),知 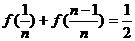
∴①+②,得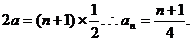 ………………8分
………………8分
(Ⅲ)∵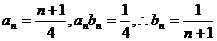
∴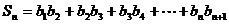
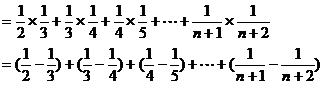
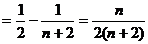
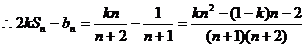 ………………………………12分
………………………………12分
由条件,可知当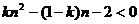 恒成立时即可满足条件
恒成立时即可满足条件
设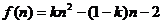
当k>0时,又二次函数的性质知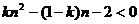 不可能成立
不可能成立
当k=0时,f(n)=-n-2<0恒成立;
当k<0时,由于对称轴直线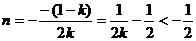
∴f(n)在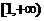 上为单调递减函数
上为单调递减函数
∴只要f(1)<0,即可满足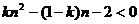 恒成立
恒成立
∴由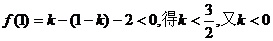 ,∴k<0
,∴k<0
综上知,k≤0,不等式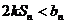 恒成立………………………………14分
恒成立………………………………14分
4、解:(1)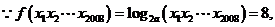
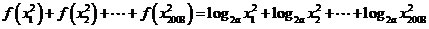
=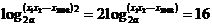 ………………………..5分
………………………..5分
(2)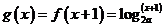 ;
;
设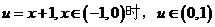 ;
;
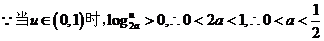 ;
;
即所求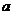 的取值范围为
的取值范围为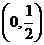 ……………….9分
……………….9分
(3) 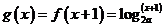 ;
;
设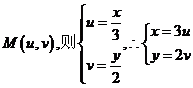 ;………………………11分
;………………………11分
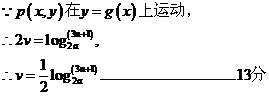
即所求函数的解析式为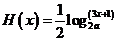 ……………………14分
……………………14分
3、解:(Ⅰ)设这二次函数f(x)=ax2+bx (a≠0) ,则 f`(x)=2ax+b,由于f`(x)=6x-2,得
a=3 , b=-2, 所以 f(x)=3x2-2x.
又因为点 均在函数
均在函数 的图像上,所以
的图像上,所以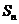 =3n2-2n.
=3n2-2n.
当n≥2时,an=Sn-Sn-1=(3n2-2n)-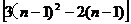 =6n-5.
=6n-5.
当n=1时,a1=S1=3×12-2=6×1-5,所以,an=6n-5 (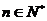 )
)
(Ⅱ)由(Ⅰ)得知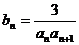 =
=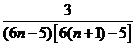 =
=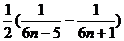 ,
,
故Tn=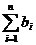 =
=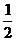
 =
=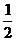 (1-
(1-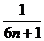 )
)
因此,要使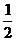 (1-
(1-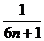 )<
)<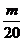 (
(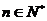 )成立的m,必须且仅须满足
)成立的m,必须且仅须满足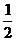 ≤
≤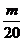 ,即m≥10,所以满足要求的最小正整数m为10.
,即m≥10,所以满足要求的最小正整数m为10.
2、解:∵f¢ (x)=4a0x3+3a1x2+2a2x+a3为偶函数,∴ f ¢(-x) = f ¢(x),
∴ -4a0x3 +3a1x2 -2a2x + a3 = 4a0x3+3a1x2 +2a2x + a3,
∴ 4a0x3 + 2a2x =0对一切x Î R恒成立,
∴ a0=a2=0,∴f (x)=a1x3+a3x
又当x=-时,f (x)取得极大值
∴ 解得∴f (x)=x3-x,f¢ (x)=2x2-1 4分
⑵解:设所求两点的横坐标为x1、x2 (x1 < x2),则(2x12-1)(2x22-1)=-1
又∵x1,x2∈[-1,1],∴2x12-1∈[-1,1],2x22-1∈[-1,1]
∴2x12-1,2x22-1中有一个为1,一个为-1,
∴或 ,∴所求的两点为(0,0)与(1,-)或(0,0)与(-1,)。
⑶证明:易知sin x∈[-1,1],cos x∈[-1,1]。
当0< x < 时,f ¢ (x) < 0;当 < x < 1时,f ¢ (x)>0。
∴f (x)在[0,]为减函数,在[,1]上为增函数,
又f (0)=0,f ()=- ,f (1)=-,而f (x)在[-1,1]上为奇函数,
∴f (x)在[-1,1]上最大值为,最小值为-,即 | f (x) | ≤ ,
∴| f (sin x) | ≤ ,| f (cos x)| ≤ , ∴| f (sin x)-f (cos x)| ≤ | f (sin x)|+| f (cos x) | ≤
1、解:(Ⅰ)∵不等式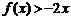 的解集为
的解集为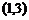
∴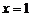 和
和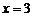 是方程
是方程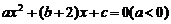 的两根 -----------1分
的两根 -----------1分
∴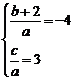 -----------2分
-----------2分
∴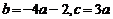 -----------3分
-----------3分
又方程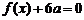 有两个相等的实根
有两个相等的实根
∴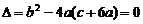 -----------4分
-----------4分
∴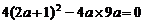
∴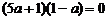
∴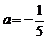 或
或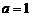 (舍)
-----------5分
(舍)
-----------5分
∴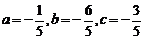 -----------6分
-----------6分
∴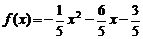 -----------7分
-----------7分
(Ⅱ)由(Ⅰ)知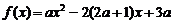
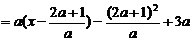
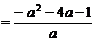 -----------9分
-----------9分
∵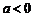 ,
,
∴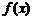 的最大值为
的最大值为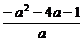 -----------11分
-----------11分
∵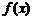 的最大值为正数
的最大值为正数
∴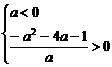
∴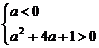 解得
解得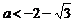 或
或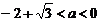 -----------13分
-----------13分
∴所求实数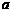 的取值范围是
的取值范围是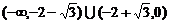 -----------14分
-----------14分
15、(2009珠海期末)已知函数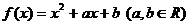 ,不等式
,不等式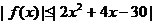 对
对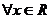 恒成立,数列
恒成立,数列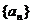 满足:
满足: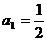 ,
, 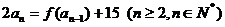 , 数列
, 数列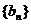 满足:
满足: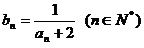 ;
;
(1)求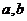 的值;
的值;
(2)设数列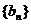 的前
的前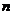 和为
和为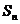 ,前
,前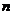 的积为
的积为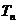 ,求
,求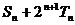 的值.
的值.
祥细答案:
14、(2009珠海期末)已知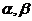 是方程
是方程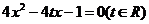 的两个实数根,函数
的两个实数根,函数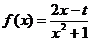 的定义域为
的定义域为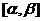 .
.
(1)判断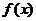 在
在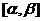 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;
(2)设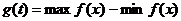 ,求函数
,求函数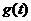 的最小值.
的最小值.
13、(2009广东潮州)抛物线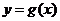 经过点
经过点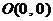 、
、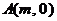 与点
与点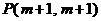 ,其中
,其中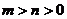 ,
,
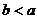 ,设函数
,设函数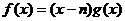 在
在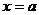 和
和 处取到极值。
处取到极值。
(1)用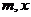 表示
表示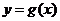 ;
;
(2)
比较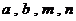 的大小(要求按从小到大排列);
的大小(要求按从小到大排列);
(3)若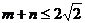 ,且过原点存在两条互相垂直的直线与曲线
,且过原点存在两条互相垂直的直线与曲线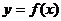 均相切,求
均相切,求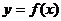 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com