
3.向量的数量积的性质:
若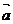 =(
=( ),b=(
),b=(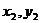 )则e·
)则e·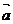 =
=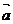 ·e=︱
·e=︱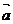 ︱cos
︱cos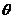 (e为单位向量);
(e为单位向量);
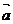 ⊥b
⊥b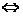
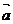 ·b=0
·b=0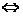
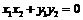 (
(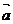 ,b为非零向量);︱
,b为非零向量);︱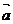 ︱=
︱=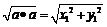 ;
;
cos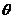 =
=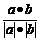 =
=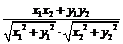 .
.
2.两个向量的数量积:
已知两个非零向量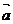 与b,它们的夹角为
与b,它们的夹角为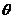 ,则
,则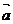 ·b=︱
·b=︱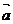 ︱·︱b︱cos
︱·︱b︱cos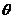 .
.
其中︱b︱cos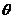 称为向量b在
称为向量b在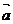 方向上的投影.
方向上的投影.
1.向量的夹角:
已知两个非零向量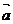 与b,作
与b,作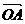 =
=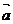 ,
, 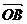 =b,则∠AOB=
=b,则∠AOB=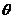 (
(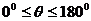 )叫做向量
)叫做向量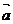 与b的夹角。
与b的夹角。
15、解:(1)方程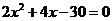 有两实根
有两实根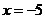 或
或 …………………………..1分
…………………………..1分
由题意知:当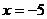 时,
时,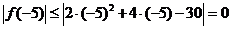 ,
,
又∵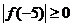 ∴
∴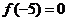 …………………………………………….3分
…………………………………………….3分
∴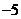 是
是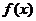 的一个零点,同理,
的一个零点,同理,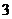 也是
也是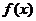 的一个零点,…………………….4分
的一个零点,…………………….4分
∴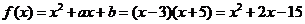 ,即
,即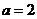 ,
,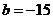 ,
,
显然,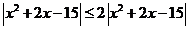 对
对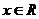 恒成立。
恒成立。
∴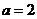 ,
,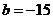 …………………………………………………………………….6分
…………………………………………………………………….6分
(2)∵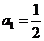 ,
,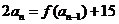 ,
,
∴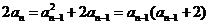 ,
,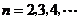 ……………………………..7分
……………………………..7分
∴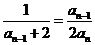 ,
,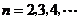 ,
,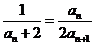 ,
,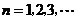
∴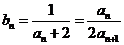 ,………………………………………………………..…..9分
,………………………………………………………..…..9分
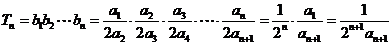 ……………...10分
……………...10分
又∵ …………….12分
…………….12分
∴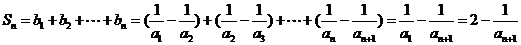
………….13分
∴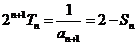 ,∴
,∴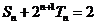 为定值。………………………..14分
为定值。………………………..14分
14、解:(1)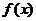 在
在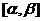 上为增函数…………………………………..1分
上为增函数…………………………………..1分
∵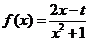 ,∴
,∴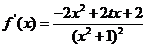 ,……….…………….3分
,……….…………….3分
∵ 当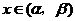 时,
时,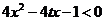 ……………………………….4分
……………………………….4分
∴ 当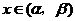 时,
时,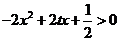 ,
,
∴当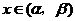 时,
时,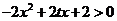 ,…………………………..5分
,…………………………..5分
∴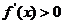 ,∴
,∴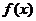 在
在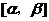 上单增。………………………6分
上单增。………………………6分
(2)由题意及(1)可知,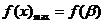 ,
,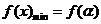 ,…………………7分
,…………………7分
∴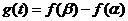
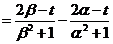
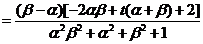 ……..8分
……..8分
∵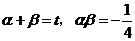 ,∴
,∴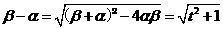 ,……………..9分
,……………..9分
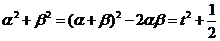 ,
,
∴ …………………………………………………..10分
…………………………………………………..10分
令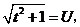 则
则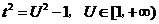
∴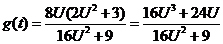 ,……………………………………………11分
,……………………………………………11分
∵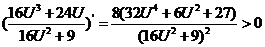 ………………………………..…….12分
………………………………..…….12分
∴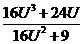 在
在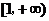 单增,……………………………………..……………..13分
单增,……………………………………..……………..13分
∴当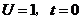 时,
时, 。………………………………………………..14分
。………………………………………………..14分
13、解:(1)由抛物线经过点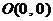 、
、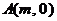 设抛物线方程
设抛物线方程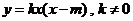 ,
,
又抛物线过点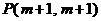 ,则
,则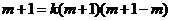 ,得
,得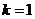 ,
,
所以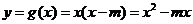 。
…………………… 3分
。
…………………… 3分
(2)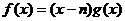
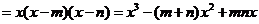 ,
,
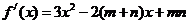 ,函数
,函数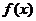 在
在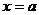 和
和 处取到极值,…… 5分
处取到极值,…… 5分
故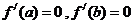 ,
,
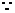
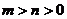 ,
,
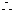
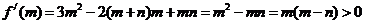 ………… 7分
………… 7分
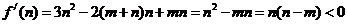
又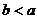 ,故
,故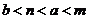 。
…… 8分
。
…… 8分
(3)设切点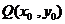 ,则切线的斜率
,则切线的斜率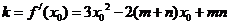
又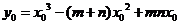 ,所以切线的方程是
,所以切线的方程是
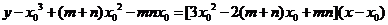 …… 9分
…… 9分
又切线过原点,故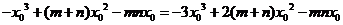
所以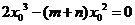 ,解得
,解得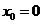 ,或
,或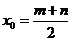 。 ………… 10分
。 ………… 10分
两条切线的斜率为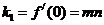 ,
,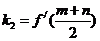 ,
,
由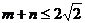 ,得
,得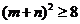 ,
,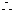
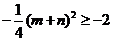 ,
,
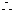
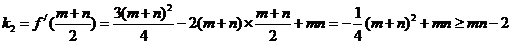 ,
,
………………………… 12分
所以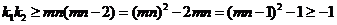 ,
,
又两条切线垂直,故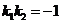 ,所以上式等号成立,有
,所以上式等号成立,有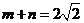 ,且
,且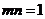 。
。
所以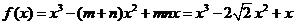 。
………… 14 分
。
………… 14 分
12、解:由 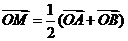 ,得点
,得点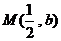 是
是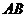 的中点,
的中点,
则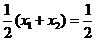 , 故
, 故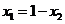 ,
,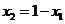 ,………… 4分
,………… 4分
所以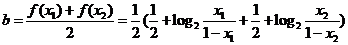
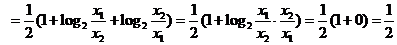 …… 6分
…… 6分
(2)由(1)知当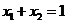 时,
时,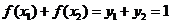 。
…… 8分
。
…… 8分
又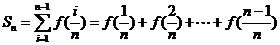 , ………… 10分
, ………… 10分
∴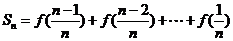 ,
,
∴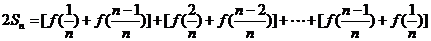
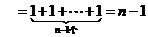 …………… 13分
…………… 13分
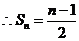 (
(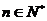 ,且
,且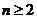 ) …………… 14分
) …………… 14分
10、解:(1)当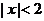 时,由
时,由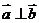 得
得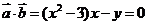 ,
,
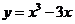 ;(
;(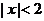 且
且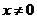 )------------------------------------------------------2分
)------------------------------------------------------2分
当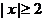 时,由
时,由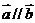 .得
.得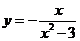 --------------------------------------4分
--------------------------------------4分
∴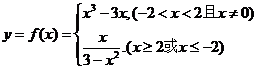 ---------------------------5分
---------------------------5分
(2)当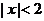 且
且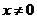 时,由
时,由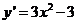 <0,解得
<0,解得 ,---------------6分
,---------------6分
当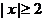 时,
时, ------------------------------8分
------------------------------8分
∴函数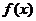 的单调减区间为(-1,0)和(0,1)---------------------------------------9分
的单调减区间为(-1,0)和(0,1)---------------------------------------9分
(3)对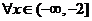
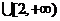 ,都有
,都有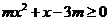 即
即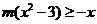 ,也就是
,也就是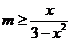 对
对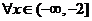
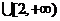 恒成立,-------------------------------------------11分
恒成立,-------------------------------------------11分
由(2)知当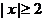 时,
时,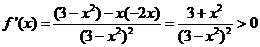
∴函数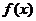 在
在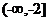 和
和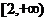 都单调递增-----------------------------------------------12分
都单调递增-----------------------------------------------12分
又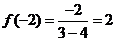 ,
,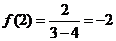
当 时
时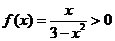 ,∴当
,∴当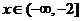 时,
时,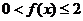
同理可得,当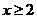 时,有
时,有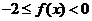 ,
,
综上所述得,对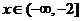
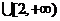 ,
, 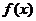 取得最大值2;
取得最大值2;
∴实数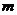 的取值范围为
的取值范围为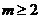 .----------------------------------------------------------------14分
.----------------------------------------------------------------14分
11(1)解:函数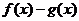 有一个零点为5,即方程
有一个零点为5,即方程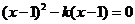 ,有一个根为5,将
,有一个根为5,将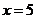 代入方程得
代入方程得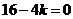 ,∴
,∴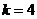 ,∴
,∴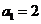 ---------------1分
---------------1分
由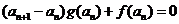 得
得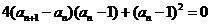
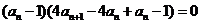
∴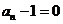 或
或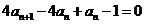 -------------------------------3分
-------------------------------3分
由(1)知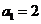 ,∴
,∴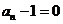 不合舍去
不合舍去
由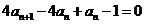 得
得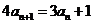 ---------------------------4分
---------------------------4分
方法1:由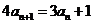 得
得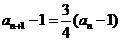 ----------------------5分
----------------------5分
∴数列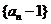 是首项为
是首项为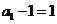 ,公比为
,公比为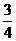 的等比数列
的等比数列
∴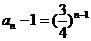 ,∴
,∴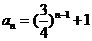 -------------------------------6分
-------------------------------6分
(方法2:由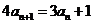 ---①得当
---①得当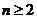 时
时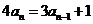 ----②
----②
①-②得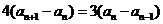
∴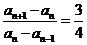 (
(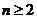 )即数列
)即数列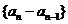 是首项为
是首项为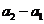 ,公比为
,公比为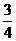 的等比数列
的等比数列
∵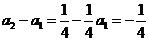 ,∴
,∴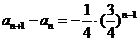 ---------------③
---------------③
由①得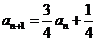 代入③整理得
代入③整理得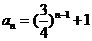 )
)
(2)由(1)知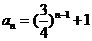
∴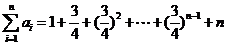 =
=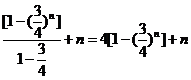 ------8分
------8分
∵对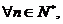 有
有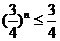 ,∴
,∴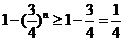
∴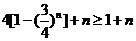 ,即
,即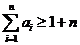 ---------------------------------------------10分
---------------------------------------------10分
(3)由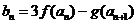 得
得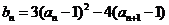
∴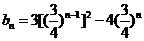 =
=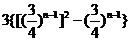 -----------------------11分
-----------------------11分
令 ,则
,则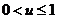 ,
,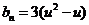 =
=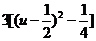
∵函数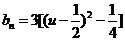 在
在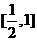 上为增函数,在
上为增函数,在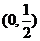 上为减函数-----12分
上为减函数-----12分
当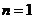 时
时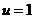 ,当
,当 时
时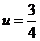 ,当
,当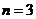 时,
时,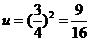 ,当
,当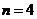 时
时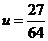 ,
,
∵
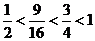 ,且
,且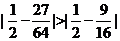
∴当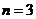 时,
时,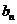 有最小值,即数列
有最小值,即数列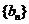 有最小项,最小项为
有最小项,最小项为
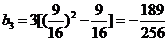 --------------------------------------------------------13分
--------------------------------------------------------13分
当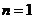 即
即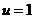 时,
时,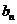 有最大值,即数列
有最大值,即数列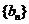 有最大项,最大项为
有最大项,最大项为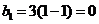 .
.
9、解:(1)证明:定义在R上的函数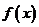 对任意的
对任意的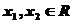 ,
,
都有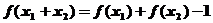 成立
成立
令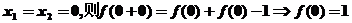 (1分)
(1分)
令
∴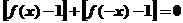 (3分)
(3分)
∴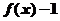 为奇函数
(4分)
为奇函数
(4分)
(2)证明:由(1)知: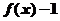 为奇函数, ∴
为奇函数, ∴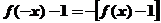 (5分)
(5分)
任取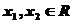 ,且
,且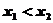 ,则
,则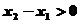
∵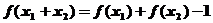
∴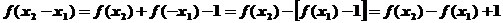
∵当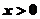 时,
时,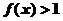 ,
,
∴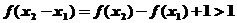 ,∴
,∴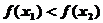 (8分)
(8分)
∴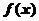 是R上的增函数。 (9分)
是R上的增函数。 (9分)
(3)解:∵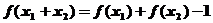 ,且
,且
∴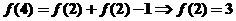 (10分)
(10分)
由不等式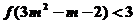 ,得
,得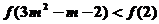 (11分)
(11分)
由(2)知: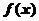 是R上的增函数
是R上的增函数
∴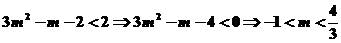 (13分)
(13分)
∴不等式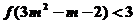 的解集为:
的解集为: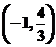 (14分)
(14分)
8、解:(I)由图形知: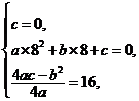 ………2分
………2分
解之,得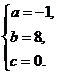 ∴函数f(x)的解析式为
∴函数f(x)的解析式为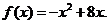 ………4分
………4分
(Ⅱ)由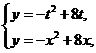 得
得 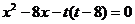 …2分
…2分
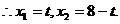 ∵0≤t≤2,
∵0≤t≤2,
∴直线l1与f(x)的图象的交点坐标为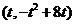 ……………3分
……………3分
由定积分的几何意义知:
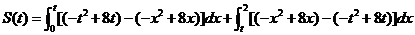 ………4分
………4分
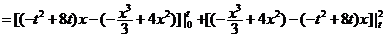
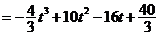 .
……………5分
.
……………5分
(Ⅲ)令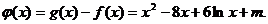
因为x>0,要使函数f(x)与函数g(x)有且仅有2个不同的交点,则函数
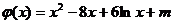 的图象与x轴的正半轴有且只有两个不同的交点.
………………1分
的图象与x轴的正半轴有且只有两个不同的交点.
………………1分
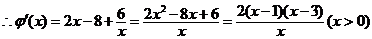 .
.
当x∈(0,1)时,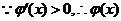 是增函数;
是增函数;
当x∈(1,3)时,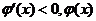 是减函数;
是减函数;
当x∈(3,+∞)时,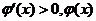 是增函数;
………………2分
是增函数;
………………2分
当x=1或x=3时,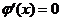 .
.
∴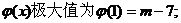
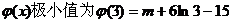 .
.
又因为当x无限趋近于零时,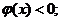 当x无限大时,
当x无限大时,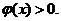
所以要使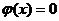 有且仅有两个不同的正根,必须且只须
有且仅有两个不同的正根,必须且只须
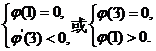 ……………………4分
……………………4分
即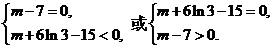 ∴m=7,或
∴m=7,或
所以当m=7或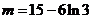 时,函数
时,函数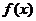 与
与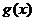 的图象有且只有两个不同交点.
…………5分
的图象有且只有两个不同交点.
…………5分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com