
1. 在统计学里,我们把所要考察对象的全体叫做总体,其中的每一个考察对象叫做个体,从总体中所抽取的一部分个体叫做总体的一个样本,样本中个体的数目叫做样本的容量.总体中所有个体的平均数叫做总体平均数,样本中所有个体的平均数叫做样本平均数.
 1
1 ?已知
?已知
 ,斜边
,斜边 //平面
//平面 ,
,
 分别与平面
分别与平面 成
成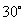 和
和 的角,已知
的角,已知 ,试求
,试求 到平面
到平面 的距离
的距离
解:作 于
于 ,
, 于
于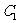 ,则由
,则由 ,得
,得
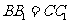 ,且
,且 就是
就是 到平面
到平面 的距离,
的距离,
设 ,连结
,连结 ,则
,则 ,
,
∴ ,在
,在 中,
中, ,
,
∴ ,∴
,∴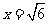 ,即
,即 到平面
到平面 的距离为
的距离为 .
.
2.已知棱长为a的正方体ABCD-A1B1C1D1,M、N分别是B1C1和C1D1的中点.
⑴求证:B1D1//平面CMN.
⑵求点B1到平面CMN的距离.
分析:显然有B1D1//MN,所以B1D1//平面CMN.
∴ 点B1到平面CMN的距离就是直线B1D1到平面CMN的距离.
∴ 可以考虑求B1D1的中点O到平面CMN的距离.
解:⑴∵ M、N分别是B1C1和C1D1的中点,∴ MN//B1D1.
而 MN 平面CMN,B1D1
平面CMN,B1D1 平面CMN,
平面CMN, ∴ B1D1//平面CMN.
∴ B1D1//平面CMN.
⑵连接AC、A1C1,A1C1交B1D1于O,交MN于E,则E是MN的中点,且MN⊥A1C1.
∵ AA1⊥平面A1B1C1D1,MN  平面CMN,
平面CMN,
∴ AA1⊥MN.
∴ MN⊥平面A1ACC1.
∴ 平面CMN⊥平面A1ACC1.
在平面A1ACC1内作OH垂直于平面CMN和平面A1ACC1的交线CE于H,则OH⊥平面CMN.
∴ OH的长就是点O到平面CMN的距离.
由⑴知,OH的长就是点B1到平面CMN的距离.
由Rt△OHE∽Rt△CC1E可得, .
.
∵ 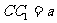 ,
, ,
,
 ,
,
∴ 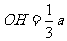 .
.
∴ 点B1到平面CMN的距离等于 .
.
说明:①由于点B1在平面CMN内的射影不易作出,所以我们就把点B1平移到点O,作出点O在平面CMN内的射影H,从而求出点B1到平面CMN的距离,这是处理点到平面的距离问题的常用手段.
②对于直线到平面的距离问题,一般取直线上的特殊点向平面上做垂线.
例1  在正方体
在正方体 中找出表示下列距离的垂线段:
中找出表示下列距离的垂线段:
(1)点 到面
到面 的距离
;
的距离
;
(2)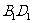 到面
到面 的距离
;
的距离
;
(3)点 到面
到面 的距离
.
的距离
.
例2.如图,已知正三角形 的边形为
的边形为 ,点D到
,点D到 各顶点的距离都是
各顶点的距离都是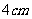 ,求点D到这个三角形所在平面的距离
,求点D到这个三角形所在平面的距离
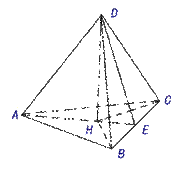 解:设
解:设 为点D在平面
为点D在平面 内的射影,延长
内的射影,延长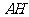 ,交
,交 于
于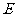 ,
,
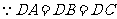 ,∴
,∴ ,
,
∴即 是
是 的中心,
的中心, 是边
是边 上的垂直平分线,
上的垂直平分线,
在 中,
中, ,
,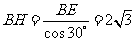 ,
,
 ,
,
即点D到这个三角形所在平面的距离是 .
.
例3.如图已知 是边长为
是边长为 的正方形,
的正方形, 分别是
分别是 的中点,
的中点, 垂直于
垂直于 所在平面,且
所在平面,且 ,求点
,求点 到平面
到平面 的距离.
的距离.
 解法一:连接
解法一:连接 交点为
交点为 ,
,
∵ 分别是
分别是 的中点,
的中点,
∴ ,
,
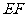 与
与 的交点为
的交点为 ,则
,则 为
为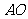 的中点,
的中点,
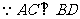 ,∴
,∴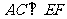 ,
,
连结 ,∵
,∵ 平面
平面 ,
,
∴ ,∴
,∴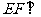 平面
平面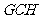 ,
,
∴平面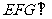 平面
平面 ,
,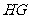 是这两个平面的交线,
是这两个平面的交线,
作 交
交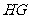 于
于 ,∴
,∴ 平面
平面 ,
,
∴线段 的长就是点
的长就是点 到平面
到平面 的距离
的距离
∵正方形 的边长为
的边长为 ,
, ,
,
∴ ,
,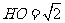 ,
, ,
,
∴ ,又
,又 ,
,
∴ ,即点
,即点 到平面
到平面 的距离为
的距离为 .
.
解法二:以 为原点,
为原点, 所在直线分别为
所在直线分别为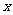 轴、
轴、 轴、
轴、 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则 ,
, ,
,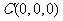 ,
,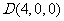 ,
, ,
, ,
,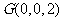
设点 在面
在面 内的射影为
内的射影为 ,
,
则
 ,
,
即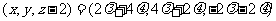 ,
,
∴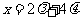 ,
, ,
, ,
,
∴ ,
,
而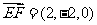 ,
, ,
,
∵ ,∴
,∴ ,
,
解得: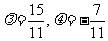 ,∴
,∴ ,∴
,∴ .
.
4.两个平行平面的距离:两个平行平面的公垂线段的长度叫做两个平行平面的距离
3.两个平行平面的公垂线、公垂线段:
(1)两个平面的公垂线:和两个平行平面同时垂直的直线,叫做两个平面的公垂线
 (2)两个平面的公垂线段:公垂线夹在平行平面间的的部分,叫做两个平面的公垂线段
(2)两个平面的公垂线段:公垂线夹在平行平面间的的部分,叫做两个平面的公垂线段
(3)两个平行平面的公垂线段都相等
(4)公垂线段小于或等于任一条夹在这两个平行平面间的线段长
2.直线到与它平行平面的距离:一条直线上的任一点到与它平行的平面的距离,叫做这条直线到平面的距离(转化为点面距离)
如果一条直线 平行与平面
平行与平面 ,则直线
,则直线 上的各点到平面的垂线段相等,即各点到
上的各点到平面的垂线段相等,即各点到 的距离相等;垂线段小于或等于
的距离相等;垂线段小于或等于 上任意一点与平面
上任意一点与平面 内任一点间的距离;
内任一点间的距离;
1.点到平面的距离:
已知点 是平面
是平面 外的任意一点,过点
外的任意一点,过点 作
作 ,垂足为
,垂足为 ,则
,则 唯一,则
唯一,则 是点
是点 到平面
到平面 的距离
的距离
即:一点到它在一个平面内的正射影的距离叫做这一点到这个平面的距离 (转化为点到点的距离)
(转化为点到点的距离)
结论:连结平面 外一点
外一点 与
与 内一点所得的线段中,垂线段
内一点所得的线段中,垂线段 最短
最短


1  两个图形
两个图形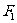 与
与 之间距离的概念:
之间距离的概念:
图形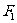 内的任一点与图形
内的任一点与图形 内的任一点间的距离中的最小值叫做图形
内的任一点间的距离中的最小值叫做图形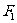 与
与 之间距离
之间距离
如:一直线和一平面相交,这条直线到这个平面的距离等于多少?
两个相交平面的距离是多少?
此题要求改正所给短文中的错误。对标有题号的每一行作出判断:如无错误,在该行右边横线上画一个勾(√);如有错误(每行只有一个错误),则按下列情况改正:
此行多一个词:把多余的词用斜线(\)划掉,在该行右边横线上写出该词,并也用斜线划掉。
此行缺一个词:在缺词处加一个漏字符号(∧),在该行右边横线上写出该加的词。
此行错一个词:在错的词下划一横线,在该行右边横线上写出改正后的词。
注意:1)原行没有错的不要改。2) 不按要求做不得分。
One day I picked out a baby bird without any feathers 76.
on my way home. The poor creature was too young to feed it, 77.
so I took it to my home and fed it as careful as I could. 78.
It kept in a birdcage made by myself and grew up day by day. 79.
I thought that it was time for the bird to return to the nature 80.
and that the forest should be its home indeed, so I set it free. 81.
To my surprise and joy, it fly down and settled on my shoulder, 82.
appeared to welcome me when I came back after school. 83.
From then on, I often saw it fly away when I left to school 84.
and fly back as I came home. We were good friend for years. 85.
第二节 书面表达(满分25分)
你的朋友李华是高中毕业生。他对填报志愿时是首先考虑专业还是学校拿不一定主意。他想了你们学校的情况。下面的表格反映了你们学校学生中存在的两种看法。
|
|
观 点 |
理 由 |
|
1 |
首先选择专业 |
1、可以学习自愿感兴趣的东西; 2、便于将来从事自己喜爱的工作。 |
|
2 |
首先选择学校 |
1、学习环境对人的成长很重要; 2、名牌大学的毕业生在求职时常会受到青睐。 |
|
3 |
你的看法…… |
请你根据此表的内容,用e-mail发给他。
注意:1、开头和结尾已给出,不计入总词数。2、词数100左右。 提示:专业 major
Dear Li Hua,
How are you?
Every student in our school as well as in your school will be faced with ther question when he passes the College-Entrance Examinations.
Yours,
Liu Wei
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com