
9.复数z=a+ai (a≠0)的辐角主值是______________。
8.z∈C,方程z -3|z|+2=0的解的个数是_____。
-3|z|+2=0的解的个数是_____。
A. 2 B. 3 C. 4 D. 5
7. 到空间不共面的4个点距离相等的平面的个数是_____。
A. 7 B. 6 C. 5 D. 4
6.方程(x -x-1)
-x-1)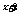 =1的整数解的个数是_____。
=1的整数解的个数是_____。
A. 1 B. 3 C. 4 D. 5
5. 函数f(x)=ax -2ax+2+b (a≠0)在闭区间[2,3]上有最大值5,最小值2,则a、b的值为_____。
-2ax+2+b (a≠0)在闭区间[2,3]上有最大值5,最小值2,则a、b的值为_____。
A. a=1,b=0 B. a=1,b=0或a=-1,b=3
C. a=-1,b=3 D. 以上答案均不正确
4. 设f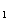 (x,y)=0是椭圆方程,f
(x,y)=0是椭圆方程,f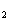 (x,y)=0是直线方程,则方程f
(x,y)=0是直线方程,则方程f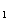 (x,y)+λf
(x,y)+λf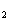 (x,y)=0 (λ∈R)表示的曲线是_____。
(x,y)=0 (λ∈R)表示的曲线是_____。
A.只能是椭圆 B.椭圆或直线 C.椭圆或一点 D.还有上述外的其它情况
3. f(x)=(a-x)|3a-x|,a是正常数,下列结论正确的是_____。
A.当x=2a时有最小值0 B.当x=3a时有最大值0
C.无最大值,且无最小值 D.有最小值但无最大值
2. 非零实数a、b、c,则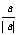 +
+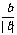 +
+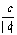 +
+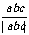 的值组成的集合是_____。
的值组成的集合是_____。
A. {-4,4} B. {0,4} C. {-4,0} D. {-4,0,4}
1. 若log
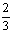 <1,则a的取值范围是_____。
<1,则a的取值范围是_____。
A. (0, 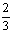 )
B. (
)
B. (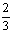 ,1)
C. (0,
,1)
C. (0, 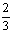 )∪(1,+∞) D. (
)∪(1,+∞) D. (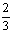 ,+∞)
,+∞)
7.过点P(2,3),且在坐标轴上的截距相等的直线方程是_____。
A. 3x-2y=0 B. x+y-5=0 C. 3x-2y=0或x+y-5=0 D.不能确定
[简解]1小题:对参数a分a>0、a=0、a<0三种情况讨论,选B;
2小题:对底数a分a>1、0<a<1两种情况讨论,选C;
3小题:分x在第一、二、三、四象限等四种情况,答案{4,-2,0};
4小题:分θ=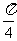 、0<θ<
、0<θ<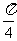 、
、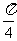 <θ<
<θ<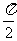 三种情况,选D;
三种情况,选D;
5小题:分x>0、x<0两种情况,选B;
6小题:分侧面矩形长、宽分别为2和4、或4和2两种情况,选D;
7小题:分截距等于零、不等于零两种情况,选C。
Ⅱ、示范性题组:
例1. 设0<x<1,a>0且a≠1,比较|log (1-x)|与|log
(1-x)|与|log (1+x)|的大小。
(1+x)|的大小。
[分析] 比较对数大小,运用对数函数的单调性,而单调性与底数a有关,所以对底数a分两类情况进行讨论。
[解] ∵ 0<x<1 ∴ 0<1-x<1 , 1+x>1
①
当0<a<1时,log (1-x)>0,log
(1-x)>0,log (1+x)<0,所以
|log
(1+x)<0,所以
|log (1-x)|-|log
(1-x)|-|log (1+x)|=log
(1+x)|=log (1-x)-[-log
(1-x)-[-log (1+x)]=log
(1+x)]=log (1-x
(1-x )>0;
)>0;
②
当a>1时,log (1-x)<0,log
(1-x)<0,log (1+x)>0,所以
|log
(1+x)>0,所以
|log (1-x)|-|log
(1-x)|-|log (1+x)|=-log
(1+x)|=-log (1-x) -log
(1-x) -log (1+x)=-log
(1+x)=-log (1-x
(1-x )>0;
)>0;
由①、②可知,|log (1-x)|>|log
(1-x)|>|log (1+x)|。
(1+x)|。
[注]本题要求对对数函数y=log x的单调性的两种情况十分熟悉,即当a>1时其是增函数,当0<a<1时其是减函数。去绝对值时要判别符号,用到了函数的单调性;最后差值的符号判断,也用到函数的单调性。
x的单调性的两种情况十分熟悉,即当a>1时其是增函数,当0<a<1时其是减函数。去绝对值时要判别符号,用到了函数的单调性;最后差值的符号判断,也用到函数的单调性。
例2. 已知集合A和集合B各含有12个元素,A∩B含有4个元素,试求同时满足下面两个条件的集合C的个数:
①. C A∪B且C中含有3个元素; ②. C∩A≠φ
。
A∪B且C中含有3个元素; ②. C∩A≠φ
。
[分析] 由已知并结合集合的概念,C中的元素分两类:①属于A 元素;②不属于A而属于B的元素。并由含A中元素的个数1、2、3,而将取法分三种。
[解]
C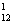 ·C
·C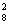 +C
+C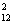 ·C
·C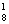 +C
+C ·C
·C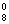 =1084
=1084
[注]本题是排列组合中“包含与排除”的基本问题,正确地解题的前提是合理科学的分类,达到分类完整及每类互斥的要求,还有一个关键是要确定C中元素如何取法。另一种解题思路是直接使用“排除法”,即C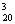 -C
-C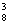 =1084。
=1084。
例3. 设{a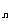 }是由正数组成的等比数列,S
}是由正数组成的等比数列,S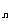 是前n项和。 ①. 证明:
是前n项和。 ①. 证明: 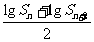 <lgS
<lgS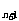 ; ②.是否存在常数c>0,使得
; ②.是否存在常数c>0,使得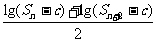 =lg(S
=lg(S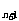 -c)成立?并证明结论。(95年全国理)
-c)成立?并证明结论。(95年全国理)
[分析] 要证的不等式和讨论的等式可以进行等价变形;再应用比较法而求解。其中在应用等比数列前n项和的公式时,由于公式的要求,分q=1和q≠1两种情况。
[解] 设{a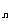 }的公比q,则a
}的公比q,则a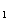 >0,q>0
>0,q>0
①.当q=1时,S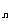 =na
=na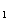 ,从而S
,从而S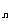 S
S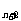 -S
-S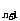
 =na
=na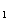 (n+2)a
(n+2)a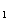 -(n+1)
-(n+1) a
a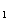
 =-a
=-a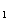
 <0;
<0;
当q≠1时,S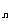 =
=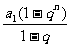 ,从而
,从而
S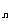 S
S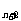 -S
-S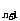
 =
=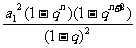 -
- =-a
=-a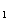
 q
q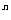 <0;
<0;
由上可得S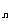 S
S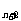 <S
<S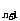
 ,所以lg(S
,所以lg(S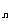 S
S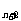 )<lg(S
)<lg(S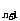
 ),即
),即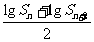 <lgS
<lgS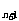 。
。
②. 要使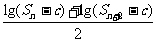 =lg(S
=lg(S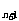 -c)成立,则必有(S
-c)成立,则必有(S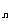 -c)(S
-c)(S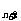 -c)=(S
-c)=(S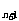 -c)
-c) ,
,
分两种情况讨论如下:
当q=1时,S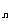 =na
=na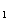 ,则
,则
(S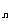 -c)(S
-c)(S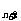 -c)-(S
-c)-(S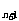 -c)
-c) =(na
=(na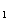 -c)[(n+2)a
-c)[(n+2)a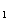 -c]-[(n+1)a
-c]-[(n+1)a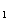 -c]
-c] =-a
=-a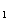
 <0
<0
当q≠1时,S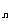 =
=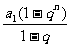 ,则(S
,则(S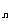 -c)(S
-c)(S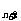 -c)-(S
-c)-(S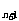 -c)
-c) =[
=[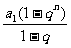 -c][
-c][  -c]-[
-c]-[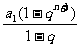 -c]
-c] =-a
=-a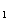 q
q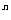 [a
[a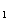 -c(1-q)]
-c(1-q)]
∵
a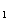 q
q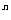 ≠0 ∴ a
≠0 ∴ a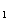 -c(1-q)=0即c=
-c(1-q)=0即c=
而S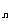 -c=S
-c=S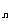 -
- =-
=-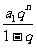 <0 ∴对数式无意义
<0 ∴对数式无意义
由上综述,不存在常数c>0, 使得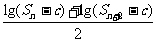 =lg(S
=lg(S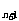 -c)成立。
-c)成立。
[注] 本例由所用公式的适用范围而导致分类讨论。该题文科考生改问题为:证明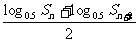 >log
>log S
S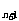 ,和理科第一问类似,只是所利用的是底数是0.5时,对数函数为单调递减。
,和理科第一问类似,只是所利用的是底数是0.5时,对数函数为单调递减。
例1、例2、例3属于涉及到数学概念、定理、公式、运算性质、法则等是分类讨论的问题或者分类给出的,我们解决时按要求进行分类,即题型为概念、性质型。
例4. 设函数f(x)=ax -2x+2,对于满足1<x<4的一切x值都有f(x)>0,求实数a的取值范围。
-2x+2,对于满足1<x<4的一切x值都有f(x)>0,求实数a的取值范围。
       1 4 x
1 4 x
1 4 x
1 4 x |
[分析] 含参数的一元二次函数在有界区间上的最大值、最小值等值域问题,需要先对开口方向讨论,再对其抛物线对称轴的位置与闭区间的关系进行分类讨论,最后综合得解。
[解]当a>0时,f(x)=a(x- )
) +2-
+2-
∴  或
或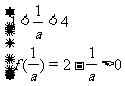
或
∴ a≥1或 <a<1或φ 即 a>
<a<1或φ 即 a> ;
;
当a<0时,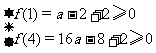 ,解得φ;
,解得φ;
当a=0时,f(x)=-2x+2, f(1)=0,f(4)=-6, ∴不合题意
由上而得,实数a的取值范围是a> 。
。
[注]本题分两级讨论,先对决定开口方向的二次项系数a分a>0、a<0、a=0三种情况,再每种情况结合二次函数的图像,在a>0时将对称轴与闭区间的关系分三种,即在闭区间左边、右边、中间。本题的解答,关键是分析符合条件的二次函数的图像,也可以看成是“数形结合法”的运用。
例5. 解不等式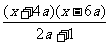 >0 (a为常数,a≠-
>0 (a为常数,a≠- )
)
[分析] 含参数的不等式,参数a决定了2a+1的符号和两根-4a、6a的大小,故对参数a分四种情况a>0、a=0、- <a<0、a<-
<a<0、a<- 分别加以讨论。
分别加以讨论。
[解] 2a+1>0时,a>- ; -4a<6a时,a>0 。 所以分以下四种情况讨论:
; -4a<6a时,a>0 。 所以分以下四种情况讨论:
当a>0时,(x+4a)(x-6a)>0,解得:x<-4a或x>6a;
当a=0时,x >0,解得:x≠0;
>0,解得:x≠0;
当- <a<0时,(x+4a)(x-6a)>0,解得:
x<6a或x>-4a;
<a<0时,(x+4a)(x-6a)>0,解得:
x<6a或x>-4a;
当a>- 时,(x+4a)(x-6a)<0,解得: 6a<x<-4a 。
时,(x+4a)(x-6a)<0,解得: 6a<x<-4a 。
综上所述,当a>0时,x<-4a或x>6a;当a=0时,x≠0;当- <a<0时,x<6a或x>-4a;当a>-
<a<0时,x<6a或x>-4a;当a>- 时,6a<x<-4a 。
时,6a<x<-4a 。
[注] 本题的关键是确定对参数a分四种情况进行讨论,做到不重不漏。一般地,遇到题目中含有参数的问题,常常结合参数的意义及对结果的影响而进行分类讨论,此种题型为含参型。
例6. 设a≥0,在复数集C中,解方程:z +2|z|=a 。 (90年全国高考)
+2|z|=a 。 (90年全国高考)
[分析]由已知z +2|z|=a和|z|∈R可以得到z
+2|z|=a和|z|∈R可以得到z ∈R,即对z分实数、纯虚数两种情况进行讨论求解。
∈R,即对z分实数、纯虚数两种情况进行讨论求解。
[解] ∵ |z|∈R,由z +2|z|=a得:z
+2|z|=a得:z ∈R; ∴ z为实数或纯虚数
∈R; ∴ z为实数或纯虚数
当z∈R时,|z| +2|z|=a,解得:|z|=-1+
+2|z|=a,解得:|z|=-1+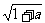 ∴ z=±(-1+
∴ z=±(-1+ );
);
当z为纯虚数时,设z=±yi
(y>0), ∴ -y +2y=a 解得:y=1±
+2y=a 解得:y=1±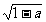 (0≤a≤1)
(0≤a≤1)
由上可得,z=±(-1+ )或±(1±
)或±(1±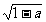 )i
)i
[注]本题用标准解法(设z=x+yi再代入原式得到一个方程组,再解方程组)过程十分繁难,而挖掘隐含,对z分两类讨论则简化了数学问题。
[另解] 设z=x+yi,代入得 x -y
-y +2
+2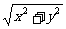 +2xyi=a;
+2xyi=a;
∴ 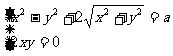
当y=0时,x +2|x|=a,解得x=±(-1+
+2|x|=a,解得x=±(-1+ ),所以z=±(-1+
),所以z=±(-1+ );
);
当x=0时,-y +2|y|=a,解得y=±(1±
+2|y|=a,解得y=±(1±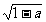 ),所以±(1±
),所以±(1±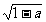 )i。
)i。
由上可得,z=±(-1+ )或±(1±
)或±(1±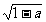 )i
)i
[注]此题属于复数问题的标准解法,即设代数形式求解。其中抓住2xy=0而分x=0和y=0两种情况进行讨论求解。实际上,每种情况中绝对值方程的求解,也渗透了分类讨论思想。
例7. 在xoy平面上给定曲线y =2x,设点A(a,0),a∈R,曲线上的点到点A的距离的最小值为f(a),求f(a)的函数表达式。 (本题难度0.40)
=2x,设点A(a,0),a∈R,曲线上的点到点A的距离的最小值为f(a),求f(a)的函数表达式。 (本题难度0.40)
[分析] 求两点间距离的最小值问题,先用公式建立目标函数,转化为二次函数在约束条件x≥0下的最小值问题,而引起对参数a的取值讨论。
[解] 设M(x,y)为曲线y =2x上任意一点,则
=2x上任意一点,则
|MA| =(x-a)
=(x-a) +y
+y =(x-a)
=(x-a) +2x=x
+2x=x -2(a-1)x+a
-2(a-1)x+a =[x-(a-1)]
=[x-(a-1)] +(2a-1)
+(2a-1)
由于y =2x限定x≥0,所以分以下情况讨论:
=2x限定x≥0,所以分以下情况讨论:
当a-1≥0时,x=a-1取最小值,即|MA}
 =2a-1;
=2a-1;
当a-1<0时,x=0取最小值,即|MA}
 =a
=a ;
;
综上所述,有f(a)=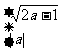
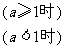 。
。
[注]本题解题的基本思路是先建立目标函数。求二次函数的最大值和最小值问题我们十分熟悉,但含参数a,以及还有隐含条件x≥0的限制,所以要从中找出正确的分类标准,从而得到d=f(a)的函数表达式。
Ⅲ、巩固性题组:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com