
142.应注意 与
与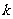 的关系:并不是
的关系:并不是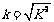 ,而
,而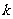 是
是 的观测值,或者说
的观测值,或者说 是一个随机变量,它在
是一个随机变量,它在 取不同的值时,
取不同的值时, 可能不同,而
可能不同,而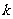 是取定一组数
是取定一组数 后的一个确定的值。
后的一个确定的值。
141.你还得相关指数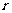 、回归系数
、回归系数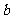 、残差平方和、的计算公式吗?
、残差平方和、的计算公式吗?
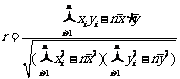 ,
,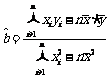 。
。
例如:同一资料,如果将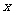 作自变量,
作自变量, 作为因变量,得到回归系数
作为因变量,得到回归系数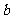 ;若将
;若将 作为变量,
作为变量,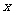 作为因变量,得到回归系数
作为因变量,得到回归系数 ;则相关系数
;则相关系数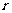 与
与 的关系是 。(
的关系是 。(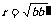 )
)
140.相关指数 来刻划回归效果的,其计算公式为:
来刻划回归效果的,其计算公式为: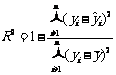 ,
, ,
, 的值越大,说明残差平方和越小,也就是说模型的拟合效果越好。
的值越大,说明残差平方和越小,也就是说模型的拟合效果越好。
139.(理)求随机变量的分布列,应按以下三个步骤进行:(1)明确随机变量的所有可能取值,以及取每个值所表示的意义;(2)利用概率的有关知识,求出随机变量每个取值的概率;(3)按规范形式写出分布列,并用分布列的性质进行检验。
138.常见的概率公式还记得吗?
例1:掷两枚骰子,求所得的点数之和为6的概率.
点数之和为6有(1,5)、(2,4)、(3,3)、(4,2)、(5,1)共5种,所以“所得点数之和为6”的概率为P= .
.
例2: 甲投篮命中率为0.8,乙投篮命中率为0.7,每人投3次,两人恰好都命中2次的概率是多少?
错解 设“甲恰好投中两次”为事件A,“乙恰好投中两次”为事件B,则两人都恰好投中两次为事件A+B,P(A+B)=P(A)+P(B): 
剖析 本题错误的原因是把相互独立同时发生的事件当成互斥事件来考虑,将两人都恰好投中2次理解为“甲恰好投中两次”与“乙恰好投中两次”的和.
正确解答:设“甲恰好投中两次”为事件A,“乙恰好投中两次”为事件B,且A,B相互独立,则两人都恰好投中两次为事件A·B,于是P(A·B)=P(A)×P(B)= 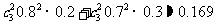 .
.
例3: 某家庭电话在家中有人时,打进的电话响第一声时被接的概率为0.1,响第二声时被接的概率为O.3,响第三声时被接的概率为0.4,响第四声时被接的概率为0.1,那么电话在响前4声内被接的概率是多少?
错解 分别记“电话响第一、二、三、四声时被接”为事件A1、A2、A3、A4,且P(A1)=0.1,
P(A2)=0.3,P(A3)=O.4,P(A4)=0.1,则电话在响前4声内被接的概率为P=P(A1)·P(A2)·
P(A3)·P(A4)=0.1×0.3×0.4×0.1=0.0012.
剖析 本题错解的原因在于把互斥事件当成相互独立同时发生的事件来考虑.根据实际生活中的经验电话在响前4声内,每一声是否被接彼此互斥.所以,P=P(A1)十P(A2)+P(A3)+P(A4)=0.1+0.3+0.4+0.1=0.9.
137.(理)随机变量的期望和方差公式你记住了吗?
136.简单随机抽样和分层抽样的共同点是每个个体被抽到的概率相等。
135.(理)公式P(A+B)=P(A)+P(B),P(AB)=P(A)P(B)的适用条件是什么?
134.(理)注意二项式的一些特性(如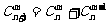 ;
; ;
;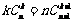 )。
)。
133.(理)求二项展开式各项系数代数和的有关问题中的“赋值法”、“转化法”,求特定项的“通项公式法”、“结构分析法”你会用吗?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com