
5、若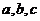 成等比数列,则函数
成等比数列,则函数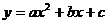 的图象与
的图象与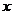 轴交点个数是
轴交点个数是
A、0 B、1 C、2 D、0或2
3、设数列 为等比数列,则下面四个数列:①
为等比数列,则下面四个数列:①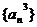 ;②
;② (
(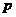 是非零常数);③
是非零常数);③ ;④
;④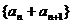 ,其中等比数列的个数为( )
,其中等比数列的个数为( )
A、1 B、2 C、3 D、4
4数列0,0,0,…,0,…( )
A、是等比数列但不是等差数列 B、是等差数列但不是等比数列
C、既是等差数列又是等比数列 D、既不是等差数列又不是等比数列

 探究1:根据图中框图,写出所打印数列的前5项,并建立数列的递推公式,这个数列是等比数列吗?
探究1:根据图中框图,写出所打印数列的前5项,并建立数列的递推公式,这个数列是等比数列吗?

解:若将打印出来的数依次记为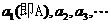 ,由图可知,
,由图可知,




于是可得递推公式
探究2:一个等比数列的第3项和第4项分别是12和18,求它的第1项和第2项;
解:设________________________________________
由已知得
探究3:已知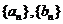 是项数相同的等比数列,仿照下表中的例子填写表格,从中你能得出什么结论?证明你的结论;
是项数相同的等比数列,仿照下表中的例子填写表格,从中你能得出什么结论?证明你的结论;
|
|
 |
 |
 |
判断数列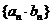 是否等比数列 是否等比数列 |
|
例 |
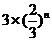 |
 |
 |
是 |
|
自选1 |
|
|
|
|
|
自选2 |
|
|
|
|
解:填表请同学们自己完成;
根据这个表格,我们可以得到:________________________________
证明如下:
变式训练1:如果 是等比数列,c是不等于0的常数,那么数列
是等比数列,c是不等于0的常数,那么数列 是等比数列吗?并证明你的结论;
是等比数列吗?并证明你的结论;
变式训练2:对于探究3中的等比数列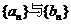 ,数列
,数列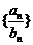 也一定是等比数列吗?并证明你的结论;
也一定是等比数列吗?并证明你的结论;
课内练习:当数列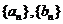 是项数相同的两个等差数列时,数列
是项数相同的两个等差数列时,数列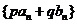 (其中
(其中 是常数)也是等差数列吗?并证明你的结论;
是常数)也是等差数列吗?并证明你的结论;
课后活动:
1等比数列 的各项均为正数,且
的各项均为正数,且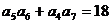 则
则 ( )
( )
A、12
B、10 C、8
D、
2、已知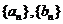 都是等比数列,那么( )
都是等比数列,那么( )
A、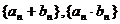 都一定是等比数列 B、
都一定是等比数列 B、 一定是等比数列,但
一定是等比数列,但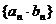 不一定是等比数列 C、
不一定是等比数列 C、 不一定是等比数列,但
不一定是等比数列,但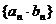 一定是等比数列 D、
一定是等比数列 D、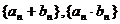 都不一定是等比数列
都不一定是等比数列
3、证明等比数列性质2;
2、证明等比数列性质1;
1、等差数列与等比数列对照表:
|
名称 |
等差数列 |
等比数列 |
|
定义式 |
|
|
|
通项公式 |
|
|
|
中项公式 |
|
|
|
性质1 |
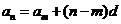 |
|
|
性质2 |
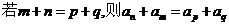 |
|
7.判断y=-Asin(ωx+ )(ω>0)的单调区间,只需求y=Asin(ωx+
)(ω>0)的单调区间,只需求y=Asin(ωx+ )的相反区间即可,一般常用数形结合.而求y=Asin(-ωx+
)的相反区间即可,一般常用数形结合.而求y=Asin(-ωx+ )(-ω<0=单调区间时,则需要先将x的系数变为正的,再设法求之.
)(-ω<0=单调区间时,则需要先将x的系数变为正的,再设法求之.
6.函数的单调性是在定义域或定义域的某个子区间上考虑的,要比较两三角函数值的大小一般先将它们化归为同一单调区间的同名函数再由该函数的单调性来比较大小。
5.求三角函数式的最小正周期时,要尽可能地化为只含一个三角函数,且三角函数的次数为1的形式,否则很容易出现错误。
4.求定义域时,若需先把式子化简,一定要注意变形时x的取值范围不能发生变化。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com