
6.a≥f(x)
恒成立 a≥[f(x)]max,; a≤f(x)
恒成立
a≥[f(x)]max,; a≤f(x)
恒成立 a≤[f(x)]min;
a≤[f(x)]min;
5.方程k=f(x)有解 k∈D(D为f(x)的值域);
k∈D(D为f(x)的值域);
4.函数的周期性
(1)y=f(x)对x∈R时,f(x +a)=f(x-a) 或f(x-2a )=f(x) (a>0)恒成立,则y=f(x)是周期为2a的周期函数;
(2)若y=f(x)是偶函数,其图像又关于直线x=a对称,则f(x)是周期为2︱a︱的周期函数;
(3)若y=f(x)奇函数,其图像又关于直线x=a对称,则f(x)是周期为4︱a︱的周期函数;
(4)若y=f(x)关于点(a,0),(b,0)对称,则f(x)是周期为2 的周期函数;
的周期函数;
(5)y=f(x)的图象关于直线x=a,x=b(a≠b)对称,则函数y=f(x)是周期为2 的周期函数;
的周期函数;
(6)y=f(x)对x∈R时,f(x+a)=-f(x)(或f(x+a)= 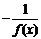 ,则y=f(x)是周期为2
,则y=f(x)是周期为2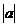 的周期函数;
的周期函数;
3.函数图像(或方程曲线的对称性)
(1)证明函数图像的对称性,即证明图像上任意点关于对称中心(对称轴)的对称点仍在图像上;
(2)证明图像C1与C2的对称性,即证明C1上任意点关于对称中心(对称轴)的对称点仍在C2上,反之亦然;
(3)曲线C1:f(x,y)=0,关于y=x+a(y=-x+a)的对称曲线C2的方程为f(y-a,x+a)=0(或f(-y+a,-x+a)=0);
(4)曲线C1:f(x,y)=0关于点(a,b)的对称曲线C2方程为:f(2a-x,2b-y)=0;
(5)若函数y=f(x)对x∈R时,f(a+x)=f(a-x)恒成立,则y=f(x)图像关于直线x=a对称;
(6)函数y=f(x-a)与y=f(b-x)的图像关于直线x= 对称;
对称;
2.函数的奇偶性
(1)若f(x)是偶函数,那么f(x)=f(-x)= ;
;
(2)若f(x)是奇函数,0在其定义域内,则 (可用于求参数);
(可用于求参数);
(3)判断函数奇偶性可用定义的等价形式:f(x)±f(-x)=0或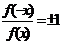 (f(x)≠0);
(f(x)≠0);
(4)若所给函数的解析式较为复杂,应先化简,再判断其奇偶性;
(5)奇函数在对称的单调区间内有相同的单调性;偶函数在对称的单调区间内有相反的单调性;
1.复合函数的有关问题
(1)复合函数定义域求法:若已知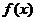 的定义域为[a,b],其复合函数f[g(x)]的定义域由不等式a≤g(x)≤b解出即可;若已知f[g(x)]的定义域为[a,b],求 f(x)的定义域,相当于x∈[a,b]时,求g(x)的值域(即
f(x)的定义域);研究函数的问题一定要注意定义域优先的原则。
的定义域为[a,b],其复合函数f[g(x)]的定义域由不等式a≤g(x)≤b解出即可;若已知f[g(x)]的定义域为[a,b],求 f(x)的定义域,相当于x∈[a,b]时,求g(x)的值域(即
f(x)的定义域);研究函数的问题一定要注意定义域优先的原则。
(2)复合函数的单调性由“同增异减”判定;
6.(1)含n个元素的集合的子集个数为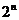 ,真子集(非空子集)个数为
,真子集(非空子集)个数为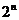 -1;
-1;
(2) (3)
(3)
5.判断命题充要条件的三种方法:(1)定义法;(2)利用集合间的包含关系判断,若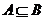 ,则A是B的充分条件或B是A的必要条件;若A=B,则A是B的充要条件;(3)等价法:即利用等价关系
,则A是B的充分条件或B是A的必要条件;若A=B,则A是B的充要条件;(3)等价法:即利用等价关系 判断,对于条件或结论是不等关系(或否定式)的命题,一般运用等价法;
判断,对于条件或结论是不等关系(或否定式)的命题,一般运用等价法;
4.判断命题的真假要以真值表为依据。原命题与其逆否命题是等价命题 ,逆命题与其否命题是等价命题 ,一真俱真,一假俱假,当一个命题的真假不易判断时,可考虑判断其等价命题的真假;
3.一个语句是否为命题,关键要看能否判断真假,陈述句、反诘问句都是命题,而祁使句、疑问句、感叹句都不是命题;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com