
3. 在等差数列{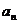 }中,有关Sn 的最值问题:(1)当
}中,有关Sn 的最值问题:(1)当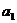 >0,d<0时,满足
>0,d<0时,满足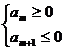 的项数m使得
的项数m使得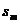 取最大值. (2)当
取最大值. (2)当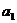 <0,d>0时,满足
<0,d>0时,满足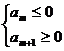 的项数m使得
的项数m使得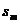 取最小值。在解含绝对值的数列最值问题时,注意转化思想的应用。
取最小值。在解含绝对值的数列最值问题时,注意转化思想的应用。
2. 判断和证明数列是等差(等比)数列常有三种方法:(1)定义法:对于n≥2的任意自然数,验证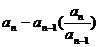 为同一常数。(2)通项公式法。(3)中项公式法:验证
为同一常数。(2)通项公式法。(3)中项公式法:验证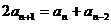
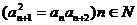 都成立。
都成立。
1. 等差数列和等比数列的概念、有关公式和性质
|
|
等差数列 |
等比数列 |
|
|
定义 |
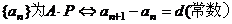 |
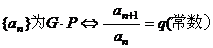 |
|
|
通项公式 |
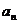 = =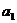 +(n-1)d= +(n-1)d=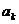 +(n-k)d= +(n-k)d=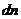 + +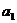 -d -d |
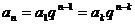 |
|
|
求和公式 |
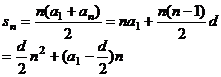 |
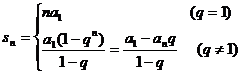 |
|
|
中项公式 |
A=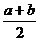 推广:2 推广:2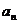 = =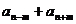 |
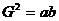 。推广: 。推广: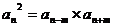 |
|
|
性质 |
1 |
若m+n=p+q则
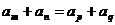 |
若m+n=p+q,则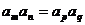 。 。 |
|
2 |
若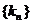 成A.P(其中 成A.P(其中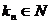 )则 )则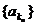 也为A.P。 也为A.P。 |
若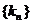 成等差数列 (其中 成等差数列 (其中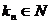 ),则 ),则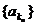 成等比数列。 成等比数列。 |
|
|
3 |
.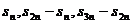 成等差数列。 成等差数列。 |
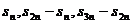 成等比数列。 成等比数列。 |
|
|
4 |
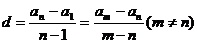 |
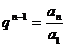 , , 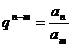 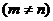 |
13. 已知数列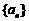 中,
中,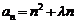 ,且
,且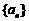 是递增数列,求实数
是递增数列,求实数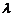 的取值范围.
的取值范围.
12. 已知数列的通项公式为 (
(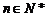 )
)
①0.98是否是它的项?
②判断此数列的增减性与有界性.
11. 已知数列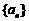 满足
满足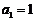 ,
,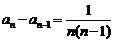
 ,求数列
,求数列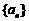 的通项公式.
的通项公式.
10. 已知数列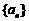 的前n项和
的前n项和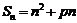 ,数列
,数列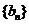 的前n项和
的前n项和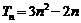 ,
,
(1)若 ,求
,求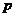 的值; (2)取数列
的值; (2)取数列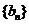 中的第1项, 第3项, 第5项,
中的第1项, 第3项, 第5项, 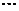 构成一个新数列
构成一个新数列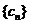 , 求数列
, 求数列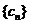 的通项公式.
的通项公式.
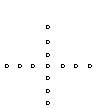
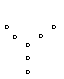
9.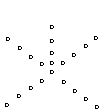 根据下列5个图形及相应点的个数的变化规律,猜测第
根据下列5个图形及相应点的个数的变化规律,猜测第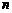 个图中有___________个点.
个图中有___________个点.
 |
|||||||
 |
|||||||
|
|||||||
 |
|||||||
(1) (2) (3) (4) (5)
8. 数列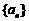 满足
满足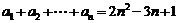 ,则
,则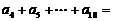 。
。
7. 数列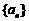 的前n项和
的前n项和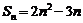 ,则
,则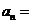 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com