
6.已知在函数y=x3+ax2-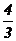 a中,
a中,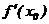 =0 且f(xo)=0, 则a的值为____________
=0 且f(xo)=0, 则a的值为____________
5.(2003年普通高等学校招生全国统一考试(上海卷理工农医类16))
f(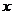 )是定义在区间[-c,c]上的奇函数,其图象如图所示:令g(
)是定义在区间[-c,c]上的奇函数,其图象如图所示:令g(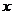 )=af(
)=af(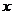 )+b,则下
)+b,则下
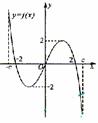 列关于函数g(
列关于函数g(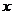 )的叙述正确的是(
)
)的叙述正确的是(
)
A.若a<0,则函数g(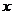 )的图象关于原点对称.
)的图象关于原点对称.
B.若a=-1,-2<b<0,则方程g(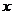 )=0有大于2的实根.
)=0有大于2的实根.
C.若a≠0,b=2,则方程g(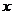 )=0有两个实根.
)=0有两个实根.
D.若a≥1,b<2,则方程g(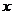 )=0有三个实根.
)=0有三个实根.
4.设f(x)在 处可导,下列式子中与
处可导,下列式子中与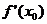 相等的是
(
)
相等的是
(
)
(1)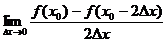 ; (2)
; (2)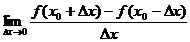 ;
;
(3)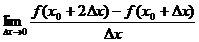 (4)
(4)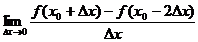 。
。
A.(1)(2) B.(1)(3) C.(2)(3) D.(1)(2)(3)(4)
3.函数y=2x3-3x2-12x+5在[0,3]上的最大值与最小值分别是 ( )
A.5 , -15 B.5 , 4 C.-4 , -15 D.5 , -16
2.对任意x,有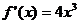 ,f(1)=-1,则此函数为
(
)
,f(1)=-1,则此函数为
(
)
A.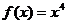 B.
B.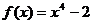 C.
C.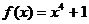 D.
D.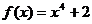
1.关于函数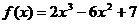 ,下列说法不正确的是
( )
,下列说法不正确的是
( )
A.在区间( ,0)内,
,0)内,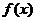 为增函数 B.在区间(0,2)内,
为增函数 B.在区间(0,2)内,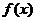 为减函数
为减函数
C.在区间(2,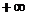 )内,
)内,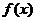 为增函数
为增函数
D.在区间( ,0)
,0)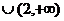 内,
内,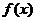 为增函数
为增函数
例6.(04年全国卷四.理22)已知函数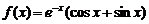 ,将满足
,将满足 的所有正数
的所有正数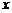 从小到大排成数列
从小到大排成数列 . (Ⅰ)证明数列
. (Ⅰ)证明数列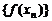 为等比数列;(Ⅱ)记
为等比数列;(Ⅱ)记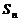 是数列
是数列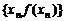 的前
的前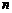 项和,求
项和,求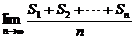 .
.
例7(03江苏)(本小题满分12分)已知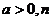 为正整数.
为正整数.
(Ⅰ)设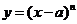 ,证明
,证明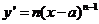 ;
;
(Ⅱ)设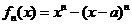 ,对任意
,对任意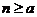 ,证明
,证明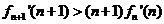 。
。
例8. (05湖北卷)已知向量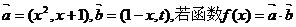 在区间(-1,1)上是增函数,求t的取值范围.
在区间(-1,1)上是增函数,求t的取值范围.
例9. (05重庆卷) 已知aÎR,讨论函数f(x)=ex(x2+ax+a+1)的极值点的个数.
例10、一艘轮船在航行中的燃料费和它的速度的立方成正比,已知在速度为每小时10公里时燃料费是每小时6元,而其他与速度无关的费用是每小时96元,问此轮船以何种速度航行时,能使行驶每公里的费用总和最小?
15. (05山东卷)已知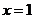 是函数
是函数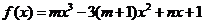 的一个极值点,其中
的一个极值点,其中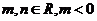 ,
,
(I)求 与
与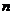 的关系式;
的关系式;
(II)求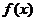 的单调区间;
的单调区间;
(III)当 时,函数
时,函数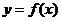 的图象上任意一点的切线斜率恒大于3
的图象上任意一点的切线斜率恒大于3 ,求
,求 的取值范围.
的取值范围.
14.(04年湖南卷.理20)已知函数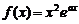 ,其中
,其中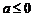 ,
,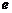 为自然对数的底数.(Ⅰ)讨论函数
为自然对数的底数.(Ⅰ)讨论函数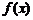 的单调性;(Ⅱ)求函数
的单调性;(Ⅱ)求函数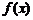 在区间
在区间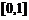 上的最大值
上的最大值
13.(04年天津卷.文21)已知函数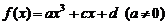 是R上的奇函数,当
是R上的奇函数,当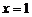 时
时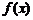 取得极值-2. (Ⅰ)求
取得极值-2. (Ⅰ)求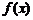 的单调区间和极大值;(Ⅱ)证明对任意
的单调区间和极大值;(Ⅱ)证明对任意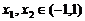 ,不等式
,不等式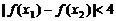 恒成立.
恒成立.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com