
3、函数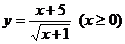 图象上最低点的坐标为…………………………(
)
图象上最低点的坐标为…………………………(
)
(A)(0,5)
(B) (3,4)
(C) (3,2)
(D) (8,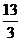 )
)
2、设a,b为实数,且a+b=3,则2a+2b的最小值是 ………………………………( )
(A)6 (B)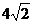 (C)
(C)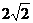 (D)8
(D)8
1、若x+2y=4,且x>0,y>0,则 lgx+lgy的最大值为 ………………………………( )
(A)2 (B)2lg2
(C)lg2
(D)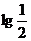
1、下列函数中,最小值为4的是……………………………………………… ( )
(A)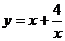 (B)
(B)
(C)  (D)
(D)

3. 运用均值不等式求最值时,要注意是否具备使用定理的条件,即"一正二定三等",三者缺一不可.
1. 不等式始终贯穿在整个中学数学之中, 诸如集合问题、方程(组)的解的讨论、 函数单调性的研究、函数的定义域、值域的确定,三角、数列、复数、立体几何、解析几何中的最大值、最小值问题, 无一不与不等式有着密切关系。
16、设a,b∈R,已知二次函数f(x)=ax2+bx+c, g(x)=cx2+bx+a,当 |x| ≤1时,|f(x)| ≤2,
(1) 求证:|g(1)| ≤2
(2) 求证:当 |x| ≤1时,|g(x)| ≤4
CBBDDAACC
15、△ABC中,利用代数换元a=y+z,b=z+x,c=x+y(x,y,z∈R+)求证:sin .
.
14、a、b、c为△ABC三边,x∈R,求证:a2x2+(a2+b2-c2)x+b2>0.
(提示:△=…=(a+b+c)(a+b-c)(a-b+c(a-b-c)<0)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com