1.要检验某卤乙烷中的卤素是否是溴元素，正确的实验方法

　 A．加入氯水振荡，观察水层是否有棕红色溴出现

B．滴入AgNO₃溶液，再加入稀HNO₃，观察有无浅黄色沉淀生成

C．加入NaOH溶液共热，冷却后加入稀HNO₃至酸性，再滴入AgNO₃溶液，观察有无浅黄色沉淀生成。

D．加入NaOH醇溶液共热，冷却后滴入AgNO₃溶液，观察有无浅黄色沉淀生成

2．基团的保护

(1)基团保护　 ①醛基的保护　 如：

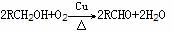
②双键的保护　　 如：

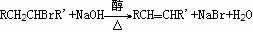
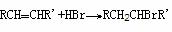
③羟基的保护　　 如：

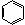　　　 R--OHR--OCH₃

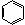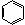 R--OCH₃R--OH

④羧基的保护　 如：

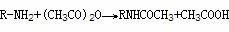
⑤氨基的保护如：

[巩固练习]

1.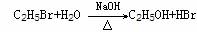基团的引入 (1)羟基的引入

①取代法 例：

②水化法 例： CH₂=CH₂ +H₂O 　　　　　　　CH₃CH₂OH

　　 ③还原法 例：CH₃CHO +H₂ CH₃CH₂OH

　　 ④氧化法 例：2CH₃CH₂CH₂CH₃+5O₂　　　　　　 4CH₃COOH+2H₂O

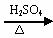
　　 ⑤水解法 例：CH₃COOCH₂CH₃+H₂O　　　　 CH₃CH₂OH+CH₃COOH　　

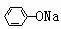
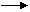　　 ⑥酸化法　 例：　　　　 + HCl　　　　　　　 +H₂O　　

(2)羟基的消去

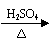
①脱水法　 例： CH₃CH₂OH　　　　　　 CH₂=CH₂ 　+H₂O

②氧化法 例： 2CH₃CH₂OH+O₂　　　　　　 2CH₃CHO +2H₂O

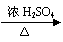③酯化法　 例：

　 CH₃CH₂OH+CH₃COOH　　　　　　 CH₃COOCH₂CH₃+H₂O　　　　　

④取代法　 例：CH₃CH₂OH +HBr　　　　　　 CH₃CH₂Br+H₂O

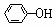
⑤中和法　 例：H₃C-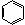-OH + NaOH　　　 H₃C--O Na +H₂O　　　　　　　

　(1)水解反应　

(2)消去反应

常温下,卤代烃中除少数为　　　　　　　 　外,大多为　　　　 或　　　　 。

卤代烃　　 　溶于水,大多数有机溶剂,某些卤代烃本身就是很好的有机溶剂。纯净的溴乙烷是

　　　　 　　(状态)，沸点38.4℃，密度比水　　　 ，　　 溶于水，易溶于乙醇等多种有机溶剂。

15．已知各项均为正数的数列{a_n}的前n项和S_n满足S₁>1，且6S_n＝(a_n+1)(a_n+2)，n∈N⁺.

(1)求{a_n}的通项公式；

(2)设数列{b_n}满足a_n(2b_n－1)＝1，并记T_n为{b_n}的前n项和，求证：3T_n+1>log₂(a_n+3)，n∈N^*.

(1)解：由a₁＝S₁＝(a₁+1)(a₁+2)，解得a₁＝1或a₁＝2，由已知a₁＝S₁>1，因此a₁＝2.

又由a_n+1＝S_n+1－S_n＝(a_n+1+1)(a_n+1+2)－(a_n+1)(a_n+2)，

得(a_n+1+a_n)(a_n+1－a_n－3)＝0，

即a_n+1－a_n－3＝0或a_n+1＝－a_n.因a_n>0，故a_n+1＝－a_n不成立，舍去．

因此a_n+1－a_n＝3.从而{a_n}是公差为3，首项为2的等差数列，故{a_n}的通项为a_n＝3n－1.

(2)证法一：由a_n(2b_n－1)＝1可解得

b_n＝log₂＝log₂；

从而T_n＝b₁+b₂+…+b_n

＝log₂.

因此3T_n+1－log₂(a_n+3)

＝log₂.

令f(n)＝³·，

则＝·³

＝.

因(3n+3)³－(3n+5)(3n+2)²＝9n+7>0，故f(n+1)>f(n)．

特别地f(n)≥f(1)＝>1.从而3T_n+1－log₂(a_n+3)＝log₂f(n)>0，即3T_n+1>log₂(a_n+3)．

证法二：同证法一求得b_n及T_n.

由二项式定理知，当c>0时，不等式(1+c)³>1+3c成立．

由此不等式有

3T_n+1＝log₂2(1+)³(1+)³…(1+)³

>log₂2(1+)(1+)…(1+)

＝log₂2···…·＝log₂(3n+2)＝log₂(a_n+3)．

证法三：同证法一求得b_n及T_n.

令A_n＝··…·，B_n＝··…·，

C_n＝··…·.

因>>，因此A>A_nB_nC_n＝.

从而3T_n+1＝log₂2(··…·)³＝log₂2A>log₂2A_nB_nC_n＝log₂(3n+2)＝log₂(a_n+3)．

证法四：同证法一求得b_n及T_n.

下面用数学归纳法证明：3T_n+1>log₂(a_n+3)．

当n＝1时，3T₁+1＝log₂，log₂(a₁+3)＝log₂5，

因此3T₁+1>log₂(a₁+3)，结论成立．

假设结论当n＝k时成立，即3T_k+1>log₂(a_k+3)，

则当n＝k+1时，

3T_k+1+1－log₂(a_k+1+3)

＝3T_k+1+3b_k+1－log₂(a_k+1+3)

>log₂(a_k+3)－log₂(a_k+1+3)+3b_k+1

＝log₂.

因(3k+3)³－(3k+5)(3k+2)²＝9k+7>0，故

log₂>0.

从而3T_k+1+1>log₂(a_k+1+3)．这就是说，当n＝k+1时结论也成立．

综上3T_n+1>log₂(a_n+3)对任何n∈N^*成立．

14．已知数列{a_n}，{b_n}满足a₁＝2，b₁＝1，且

(n≥2)

(Ⅰ)令c_n＝a_n+b_n，求数列{c_n}的通项公式．

(Ⅱ)求数列{a_n}的通项公式及前n项和公式．

解：(Ⅰ)由题设得a_n+b_n＝(a_n－1+b_n－1)+2(n≥2)，即c_n＝c_n－1+2(n≥2)．

易知{c_n}是首项为a₁+b₁＝3，公差为2的等差数列，通项公式为c_n＝2n+1.

(Ⅱ)由题设得a_n－b_n＝(a_n－1－b_n－1)(n≥2)，令d_n＝a_n－b_n

d_n＝d_n－1(n≥2)．

易知{d_n}是首项为a₁－b₁＝1，公比为的等比数列，通项公式为d_n＝.

由解得a_n＝+n+.

求和得S_n＝－++n+1.

13．数列{a_n}的前n项和为S_n，且a₁＝1，a_n+1＝S_n，n＝1,2,3，…，求：

(Ⅰ)a₂，a₃，a₄的值及数列{a_n}的通项公式；

(Ⅱ)a₂+a₄+a₆+…+a_2n的值．

解：(Ⅰ)由a₁＝1，a_n+1＝S_n，n＝1,2,3，…，得

a₂＝S₁＝a₁＝，

a₃＝S₂＝(a₁+a₂)＝，

a₄＝S₃＝(a₁+a₂+a₃)＝.

由a_n+1－a_n＝(S_n－S_n－1)＝a_n(n≥2)．

得a_n+1＝a_n(n≥2)

又a₂＝，所以a_n＝()^n－2(n≥2)．

所以，数列{a_n}的通项公式为

a_n＝　

(Ⅱ)由(Ⅰ)可知，a₂，a₄，…，a_2n，是首项为，公比为()²，项数为n的等比数列，所以a₂+a₄+a₆+…+a_2n＝·＝[()²ⁿ－1]．

12．已知数列{a_n}的前n项和为S_n，满足log₂(1+S_n)＝n+1，求数列的通项公式．

解：S_n满足log₂(1+S_n)＝n+1，∴1+S_n＝2ⁿ⁺¹，

∴S_n＝2ⁿ⁺¹－1.

∴a₁＝3，a_n＝S_n－S_n－1＝(2ⁿ⁺¹－1)－(2ⁿ－1)＝2ⁿ(n≥2)，

∴{a_n}的通项公式为a_n＝

11．(2008·北京朝阳)设函数f(x)＝a₁+a₂x+a₃x²+…+a_nx^n－1，f(0)＝，数列{a_n}满足f(1)＝n²a_n(n∈N^*)，则数列{a_n}的通项a_n等于________．

答案：

解析：由f(x)＝a₁+a₂x+a₃x²+…+a_nx^n－1，f(0)＝得a₁＝，又由数列{a_n}满足f(1)＝n²a_n(n∈N^*)得S_n＝n²a_n，也有S_n－1＝(n－1)²a_n－1，a_n＝S_n－S_n－1＝n²a_n－(n－1)²a_n－1，整理得a_n＝a_n－1，则数列{a_n}的通项a_n＝a_n－1＝·a_n－2＝…＝···…··＝，故填.