2．(1)C(1，2)　

(2)－10≤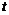≤2　

(3)S与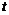的函数关系式为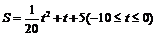或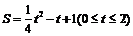　

1．A　

4．如图2-4-49，在梯形ABCD中，AB=BC=10㎝，CD=6㎝，∠C=∠D=90⁰．

(1)如图2-4-50，动点P、Q同时以每秒1㎝的速度从点B出发，点P沿BA、AD、DC运动到点C停止．设P、Q同时从点B出发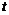秒时，△PBQ的面积为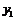(㎝²)，求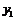(㎝²)关于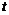(秒)的函数关系式．

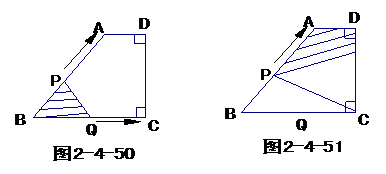
(2)如图2-4-51，动点P以每秒1㎝的速度从点B出发沿BA运动，点E在线段CD上随之运动，且PC=PE．设点P从点B出发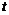秒时，四边形PADE的面积为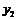(㎝²)．求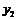(㎝²)关于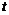(秒)的函数关系式，并写出自变量的取值范围．

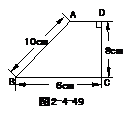
[答案]　　　　　　　 　　　　　　　　　　　　　　

3．如图2-4-48，在△ABC中，∠B=90⁰，点P从点A开始沿AB边向点B以1㎝/秒的速度移动，点Q从点B开始沿BC边向点C以2㎝/秒的速度移动．(1)如果P、Q分别从A、B同时出发，几秒后△PBQ的面积等于8㎝²？(2)如果P、Q分别从A、B同时出发，点P到达点B后又继续沿BC边向点C移动，点Q到达点C后又继续沿CA边向点A移动，在这一整个移动过程中，是否存在点P、Q，使△PBQ的面积等于9㎝²？若存在，试确定P、Q的位置；若不存在，请说明理由．

2．如图2-4-47，四边形AOBC为直角梯形，OC=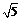，OB=%AC，OC所在直线方程为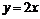，平行于OC的直线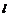为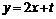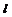：，是由A点平移到B点时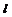，与直角梯形AOBC两边所转成的三角形的面积记为S．(1)求点C的坐标．(2)求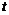的取值范围．(3)求出S与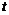之间的函数关系式．

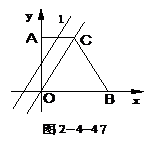
1．如图2-4-45，在ABCD中，∠DAB=60⁰，AB=5，BC=3，鼎足之势P从起点D出发，沿DC、CB向终点B匀速运动．设点P所走过的路程为，点P所以过的线段与绝无仅有AD、AP所围成图形的面积为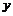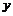，随的函数关系的变化而变化．在图2-4-46中，能正确反映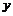与的函数关系的是(　　　　　　 )　

8．(05年南通)如图，光滑平行的水平金属导轨MN、PQ相距l，在M点和P点间接一个阻值为R的电阻，在两导轨间OO₁O₁′O′矩形区域内有垂直导轨平面竖直向下、宽为d的匀强磁场，磁感强度为B。一质量为m，电阻为r的导体棒ab，垂直搁在导轨上，与磁场左边界相距d₀。现用一大小为F、水平向右的恒力拉ab棒，使它由静止开始运动，棒ab在离开磁场前已经做匀速直线运动(棒ab与导轨始终保持良好的接触，导轨电阻不计)。求：

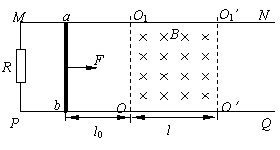(1)棒ab在离开磁场右边界时的速度；

(2)棒ab通过磁场区的过程中整个回路所消

耗的电能；

(3)试分析讨论ab棒在磁场中可能的运动情况。

答案：(1)ab棒离开磁场右边界前做匀速运动，

速度为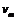，则有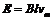　 　　　　　　　　　　　　　

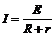
对ab棒　　 F－BIl＝0　　　

解得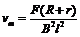　　　 　　　

(2)由能量守恒可得：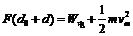　　　

解得：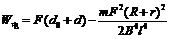　　　 　　

(3)设棒刚进入磁场时速度为v

　由　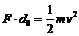 　　　　　可得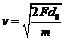　　 　　　　　

棒在进入磁场前做匀加速直线运动，在磁场中运动可分三种情况讨论：

①若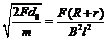(或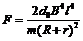)，则棒做匀速直线运动；

②若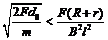(或F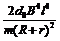＞)，则棒先加速后匀速；

③若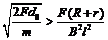(或F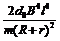＜＝，则棒先减速后匀速。

7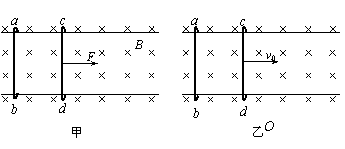．(05年宿迁)两根水平平行固定的光滑金属导轨宽为L，足够长，在其上放置两根长也为L且与导轨垂直的金属棒ab和cd，它们的质量分别为2m、m，电阻阻值均为R(金属导轨及导线的电阻均可忽略不计)，整个装置处在磁感应强度大小为B、方向竖直向下的匀强磁场中。

(1)现把金属棒ab锁定在导轨的左端，如图甲，对cd施加与导轨平行的水平向右的恒力F，使金属棒cd向右沿导轨运动，当金属棒cd的运动状态稳定时，金属棒cd的运动速度是多大？

(2)若对金属棒ab解除锁定，如图乙，使金属棒cd获得瞬时水平向右的初速度v₀，当它们的运动状态达到稳定的过程中，流过金属棒ab的电量是多少？整个过程中ab和cd相对运动的位移是多大？

答案：⑴当cd棒稳定时，恒力F和安培力大小相等，方向相反，以速度v匀速度运动，有：

F=BIL　　 又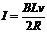　　 　　联立得： 　

　 ⑵ab棒在安培力作用下加速运动，而cd在安培力作用下减速运动，当它们的速度相同，达到稳定状态时，回路中的电流消失，ab，cd棒开始匀速运动。

设这一过程经历的时间为t，最终ab、cd的速度为v′，通过ab棒的电量为Q。

则对于ab棒由动量守恒：BILt＝2mv′　 即：BLQ＝2 mv′

同理，对于cd棒：－BILt＝mv′－mv₀　 即：　BLQ＝m(v₀-v′)得：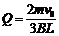

设整个过程中ab和cd的相对位移为S，由法拉第电磁感应定律得：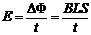　

流过ab的电量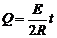：　　　　 得：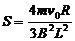

6．(05年如东)水平固定的光滑U型金属框架宽为L，足够长，其上放一质量为m的金属棒ab，左端连接有一阻值为R的电阻(金属框架、金属棒及导线的电阻均可忽略不计)，整个装置处在向下的匀强磁场中，磁感应强度大小为B。现给棒一个初速v₀，使棒始终垂直框架并沿框架运动，如图所示。

(1)金属棒从开始运动到达稳定状态的过程中求通过电阻R的电量和电阻R中产生的热量

(2)金属棒从开始运动到达稳定状态的过程中求金属棒通过的位移

(3)如果将U型金属框架左端的电阻R换为一电容为C的电容器，其他条件不变，如图所示。求金属棒从开始运动到达稳定状态时电容器的带电量和电容器所储存的能量(不计电路向外界辐射的能量)

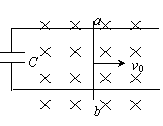
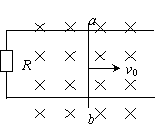
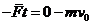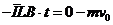答案：(1)由动量定理得　　 即　　　　 所以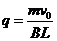

由能量守恒定律得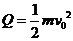

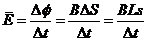
(2)　　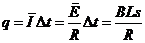 所以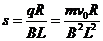

(3)当金属棒ab做切割磁力线运动时，要产生感应电动势，这样，电容器C将被充电，ab棒中有充电电流存在，ab棒受到安培力的作用而减速，

当ab棒以稳定速度v匀速运动时，BLv=U_C=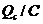

而对导体棒ab利用动量定理可得　 　-BL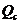=mv-mv₀

由上述二式可求得：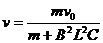 　　　　　

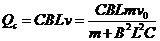
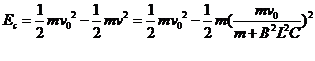
5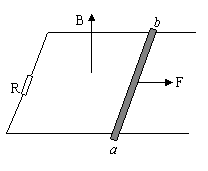．(05年南京)如右图所示，光滑的水平平行放置的导轨左端连有电阻R，导轨上架有一根裸金属棒ab，整个装置处于垂直轨道平面的匀强磁场中，今从静止起用力拉金属棒(保持棒与导轨垂直)，若拉力恒定，经时间t₁后ab的速度为v，加速度为a₁，最终速度可达2v；若拉力的功率恒定，经时间t₂后ab的速度也为v，加速度为a₂，最终速度也可达2v。求a₁和a₂满足的关系。(不计其他电阻)

答案：a₂=3a₁