
4.上、下两个底面平行且都是长方形,四个侧面都是全等的等腰梯形的六面体D
A.是不存在的 B.是正四棱台 C.是四棱台但可能不是正四棱台 D.存在但可能不是正棱台
3.一个三棱锥的所有棱长都是1,那么这个三棱锥在平面α上的射影的面积不可能是BA B
B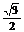 C
C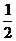 D
D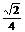
2.在等差数列{an}中,a1=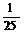 ,从第10项开始比1大,记
,从第10项开始比1大,记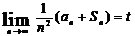 ,则t的取值范围是D
,则t的取值范围是D
A.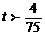 B.
B.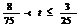 C.
C.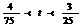 D.
D.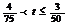
1.单位有六个科室,现招聘来4名新毕业的大学生,要随机安排到其中的两个科室且每科室2名,则不同的安排方案种数为DA.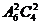 B.
B. 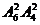 C.
C. 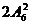 D.
D. 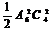
21、在数列{an},{bn}中,a1=2,
b1=4,且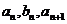 成等差数列,
成等差数列,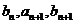 成等比数列(
成等比数列(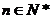 )
)
(Ⅰ)求a2, a3, a4及b2, b3, b4,由此猜测{an},{bn}的通项公式,并用数学归纳法证明你的结论;
(Ⅱ)证明: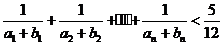
20、如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=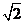 ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
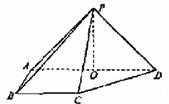
(Ⅰ)求证:PO⊥平面ABCD;
(Ⅱ)求异面直线PB与CD所成角的大小;
(Ⅲ)线段AD上是否存在点Q,使得它到平面PCD的距离为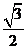 ?若存在,求出
?若存在,求出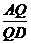 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
19.袋中有20个大小相同的球,其中记上0号的有10个,记上n号的有n个(n=1,2,3,4).现从袋中任取一球.ξ表示所取球的标号.
(Ⅰ)求ξ的分布列,期望和方差;
(Ⅱ)若η=aξ-b,Eη=1,Dη=11,试求a,b的值.
18、如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
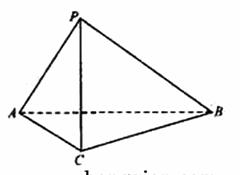
(1)求证:PC⊥AB;
(2)求二面角B-AP-C的大小;
(3)求点C到平面APB的距离.
17.甲、乙等五名奥运志愿者被随机地分到A,B,C,D四个不同的岗位服务,每个岗位至少有一名志愿者.
(Ⅰ)求甲、乙两人同时参加A岗位服务的概率;
(Ⅱ)求甲、乙两人不在同一个岗位服务的概率;
(Ⅲ)设随机变量ξ为这五名志愿者中参加A岗位服务的人数,求ξ的分布列.
16、已知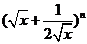 展开式中的前三项系数成等差数列,求展开式中含
展开式中的前三项系数成等差数列,求展开式中含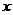 的项
的项
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com