
6.模的性质:⑴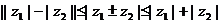 ;⑵
;⑵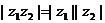 ;⑶
;⑶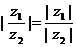 ;⑷
;⑷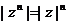 ;
;
5.共轭的性质:⑴ ;⑵
;⑵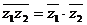 ;⑶
;⑶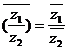 ;⑷
;⑷ 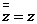 。
。
4.运算律:(1)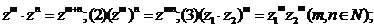
3.几个重要的结论:
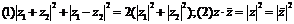 ;⑶
;⑶ ;⑷
;⑷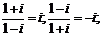
⑸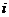 性质:T=4;
性质:T=4;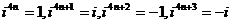 ;
;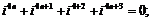
(6)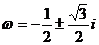 以3为周期,且
以3为周期,且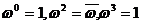 ;
;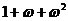 =0;
=0;
(7)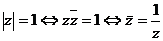 。
。
2.复数的代数形式及其运算:设z1= a + bi , z2 = c + di (a,b,c,d∈R),则:
(1) z 1±
z2 = (a + b) ±
(c + d)i;⑵ z1.z2 =
(a+bi)·(c+di)=(ac-bd)+
(ad+bc)i;⑶z1÷z2 =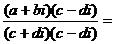
 (z2≠0) ;
(z2≠0) ;
1.概念:
⑴z=a+bi∈R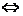 b=0 (a,b∈R)
b=0 (a,b∈R)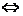 z=
z=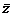
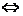 z2≥0;
z2≥0;
⑵z=a+bi是虚数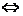 b≠0(a,b∈R);
b≠0(a,b∈R);
⑶z=a+bi是纯虚数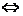 a=0且b≠0(a,b∈R)
a=0且b≠0(a,b∈R)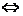 z+
z+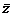 =0(z≠0)
=0(z≠0)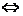 z2<0;
z2<0;
⑷a+bi=c+di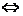 a=c且c=d(a,b,c,d∈R);
a=c且c=d(a,b,c,d∈R);
5.等差数列前n项和最值的求法:
⑴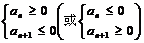 ;⑵利用二次函数的图象与性质。
;⑵利用二次函数的图象与性质。
4.前 项和的求法:⑴拆、并、裂项法;⑵倒序相加法;⑶错位相减法。
项和的求法:⑴拆、并、裂项法;⑵倒序相加法;⑶错位相减法。
2.等差、等比数列性质




 等差数列
等比数列
等差数列
等比数列

 通项公式
通项公式 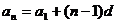

 前n项和
前n项和 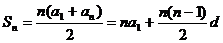
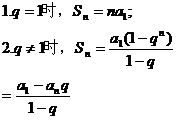
性质 ①an=am+ (n-m)d, ①an=amqn-m;
 ②m+n=p+q时am+an=ap+aq
②m+n=p+q时aman=apaq
②m+n=p+q时am+an=ap+aq
②m+n=p+q时aman=apaq
 ③
③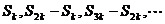 成AP ③
成AP ③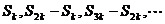 成GP
成GP

 ④
④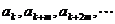 成AP,
成AP,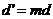 ④
④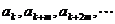 成GP,
成GP,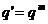
等差数列特有性质:①项数为2n时:S2n=n(an+an+1)=n(a1+a2n);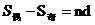 ;
;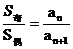 ;②项数为2n-1时:S2n-1=(2n-1)
;②项数为2n-1时:S2n-1=(2n-1)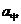 ;
;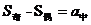 ;
;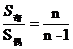 ;
;
③若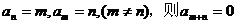 ;若
;若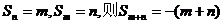 ;
;
若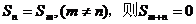 。
。
|
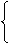
|
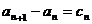 ;
;
⑷叠乘法( 型);⑸构造法(
型);⑸构造法(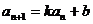 型);(6)迭代法;
型);(6)迭代法;
⑺间接法(例如: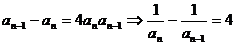 );⑻作商法(
);⑻作商法(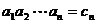 型);⑼待定系数法;⑽(理科)数学归纳法。
型);⑼待定系数法;⑽(理科)数学归纳法。
注:当遇到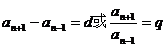 时,要分奇数项偶数项讨论,结果是分段形式。
时,要分奇数项偶数项讨论,结果是分段形式。
1.定义:
⑴等差数列 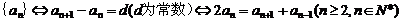
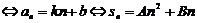 ;
;
⑵等比数列 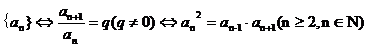
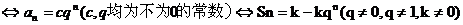 ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com