
类型Ⅴ:设二次函数ƒ(x)=ax2+bx+c(a>0)方程ƒ(x)-x=0的两个根x1,x2满足0<x1<x2<。
(Ⅰ)当X∈(0,x1)时,证明X<ƒ(x)<x1。
(Ⅱ)设函数ƒ(x)的图象关于直线x=x0对称,证明x0< 。
解题思路:
本题要证明的是x<ƒ(x),ƒ(x)<x1和x0< ,由题中所提供的信息可以联想到:①ƒ(x)=x,说明抛物线与直线y=x在第一象限内有两个不同的交点;②方程ƒ(x)-x=0可变为ax2+(b-1)x+1=0,它的两根为x1,x2,可得到x1,x2与a.b.c之间的关系式,因此解题思路明显有三条①图象法②利用一元二次方程根与系数关系③利用一元二次方程的求根公式,辅之以不等式的推导。现以思路②为例解决这道题:
(Ⅰ)先证明x<ƒ(x),令ƒ(x)=ƒ(x)-x,因为x1,x2是方程ƒ(x)-x=0的根,ƒ(x)=ax2+bx+c,所以能ƒ(x)=a(x-x1)(x-x2)
因为0<x1<x2,所以,当x∈(0,x1)时, x-x1<0, x-x2<0得(x-x1)(x-x2)>0,又a>0,因此ƒ(x) >0,即ƒ(x)-x>0.至此,证得x<ƒ(x)
根据韦达定理,有 x1x2= ∵ 0<x1<x2<,c=ax1x2<x=ƒ(x1), 又c=ƒ(0),∴ƒ(0)<ƒ(x1), 根据二次函数的性质,曲线y=ƒ(x)是开口向上的抛物线,因此,函数y=ƒ(x)在闭区间[0,x1]上的最大值在边界点x=0或x=x1处达到,而且不可能在区间的内部达到,由于ƒ(x1)>ƒ(0),所以当x∈(0,x1)时ƒ(x)<ƒ(x1)=x1,
即x<ƒ(x)<x1
|
函数ƒ(x)的图象的对称轴为直线x=- ,且是唯一的一条对称轴,因此,依题意,得x0=-,因为x1,x2是二次方程ax2+(b-1)x+c=0的根,根据违达定理得,x1+x2=-,∵x2-<0,
∴x0=-=(x1+x2-)<,即x0=。
二次函数,它有丰富的内涵和外延。作为最基本的幂函数,可以以它为代表来研究函数的性质,可以建立起函数、方程、不等式之间的联系,可以偏拟出层出不穷、灵活多变的数学问题,考查学生的数学基础知识和综合数学素质,特别是能从解答的深入程度中,区分出学生运用数学知识和思想方法解决数学问题的能力。
二次函数的内容涉及很广,本文只讨论至此,希望各位同仁在高中数学教学中也多关注这方面知识,使我们对它的研究更深入。
在高中阶阶段学习单调性时,必须让学生对二次函数y=ax2+bx+c在区间(-∞,-]及[-,+∞) 上的单调性的结论用定义进行严格的论证,使它建立在严密理论的基础上,与此同时,进一步充分利用函数图象的直观性,给学生配以适当的练习,使学生逐步自觉地利用图象学习二次函数有关的一些函数单调性。
类型Ⅲ:画出下列函数的图象,并通过图象研究其单调性。
(1)y=x2+2|x-1|-1 (2)y=|x2-1| (3)= x2+2|x|-1
这里要使学生注意这些函数与二次函数的差异和联系。掌握把含有绝对值记号的函数用分段函数去表示,然后画出其图象。
类型Ⅳ设ƒ(x)=x2-2x-1在区间[t,t+1]上的最小值是g(t)。
求:g(t)并画出 y=g(t)的图象
解:ƒ(x)=x2-2x-1=(x-1)2-2,在x=1时取最小值-2
当1∈[t,t+1]即0≤t≤1,g(t)=-2
当t>1时,g(t)=ƒ(t)=t2-2t-1
当t<0时,g(t)=ƒ(t+1)=t2-2
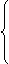 t2-2,
(t<0)
t2-2,
(t<0)
g(t)= -2,(0≤t≤1)
t2-2t-1, (t>1)
首先要使学生弄清楚题意,一般地,一个二次函数在实数集合R上或是只有最小值或是只有最大值,但当定义域发生变化时,取最大或最小值的情况也随之变化,为了巩固和熟悉这方面知识,可以再给学生补充一些练习。
如:y=3x2-5x+6(-3≤x≤-1),求该函数的值域。
初中阶段已经讲述了函数的定义,进入高中后在学习集合的基础上又学习了映射,接着重新学习函数概念,主要是用映射观点来阐明函数,这时就可以用学生已经有一定了解的函数,特别是二次函数为例来加以更深认识函数的概念。二次函数是从一个集合A(定义域)到集合B(值域)上的映射ƒ:A→B,使得集合B中的元素y=ax2+bx+c(a≠0)与集合A的元素X对应,记为ƒ(x)= ax2+ bx+c(a≠0)这里ax2+bx+c表示对应法则,又表示定义域中的元素X在值域中的象,从而使学生对函数的概念有一个较明确的认识,在学生掌握函数值的记号后,可以让学生进一步处理如下问题:
类型I:已知ƒ(x)= 2x2+x+2,求ƒ(x+1)
这里不能把ƒ(x+1)理解为x=x+1时的函数值,只能理解为自变量为x+1的函数值。
类型Ⅱ:设ƒ(x+1)=x2-4x+1,求ƒ(x)
这个问题理解为,已知对应法则ƒ下,定义域中的元素x+1的象是x2-4x+1,求定义域中元素X的象,其本质是求对应法则。
一般有两种方法:
(1)把所给表达式表示成x+1的多项式。
ƒ(x+1)=x2-4x+1=(x+1)2-6(x+1)+6,再用x代x+1得ƒ(x)=x2-6x+6
(2) 变量代换:它的适应性强,对一般函数都可适用。
令t=x+1,则x=t-1 ∴(t)=(t-1)2-4(t-1)+1=t2-6t+6从而ƒ(x)= x2-6x+6
25.The thief broke in,trying to open the safe but .
A.in vain B.in no way C.on no condition D.on purpose
答案 A
24.This study shows that languages may differ,the order in which young kids learn the parts of speech appears to be the same across different languages.
A.since B.so C.while D.but
答案 C
23.Having lived in the town for quite a few years,Mr. Johnson no longer felt among the
local people.
A.out of order B.out of place C.out of control D.out of the question
答案 B
22.Dress warmly, you’ll catch a cold.
A.on the contrary B.or rather C.or else D.in no way
答案 C
21.There is such a problem we all should .
A.as;pay attention to it B.that;attract our attention
C.as;pay attention to D.that;attract our attention to it
答案 C
20.-Susan’s head ached staring at the screen for over ten hours.
-Over ten hours!That’s really what I can imagine!
A.of;above B.in;over C.through;among D.from;beyond
答案 D
19.You can’t attend the party tonight because it is stormy. ,you still haven’t got over your high fever.
A.Therefore B.However C.Moreover D.Thus
答案 C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com